Глава 12

ФИЗИЧЕСКИЕ И ГЕОЛОГИЧЕСКИЕ ОСНОВЫ ГРАВИРАЗВЕДКИ

12.1. СИЛА ТЯЖЕСТИ. ПОТЕНЦИАЛ СИЛЫ ТЯЖЕСТИ

Сила тяжести. Основной величиной, измеряемой в гравиразведке, является ускорение свободного падения, которое для краткости называют силой тяжести. Силу тяжести, описываемую как Р=mg, относят к единичной массе, т.е. притягиваемую к Земле массу принимают равной m=1. Тогда значение силы тяжести численно равно значению ускорения свободного падении, т.е. Р=g. Силу, действующую на единичную массу, называют также напряженностью поля, следовательно, по физическому смыслу силу тяжести можно рассматривать как напряженность гравитационного поля.

Поле силы тяжести - естественное физическое поле, отображающее распределение силы тяжести Р в пространстве, которым обычно является поверхность Земли. Сила Р на поверхности в точке А представляет равнодействующую двух сил - силы притяжения 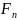и центробежной силы 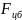, т. е. (рис. 12.1, а).

Сила притяжения между двумя точечными массам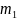и и 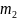, находящимися на расстоянии R, вычисляется согласно закону всемирного тяготения Ньютона:

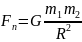(12.1)

Одной из этих масс является масса Земли, которую в первом приближении считают сосредоточенной в центре Земли, вто­рой - масса притягиваемого тела. Коэффициент G называ­ется гравитационной постоянной, величина которой равна м³/кг∙с². По физическому смыслу гравитационная по­стоянная - сила, действующая между двумя единичными масса­ми, находящимися на расстоянии одного метра.

Центробежная сила, возникающая в результате вращения Земли вокруг своей оси, направлена по нормали r к оси враще­ния и равна

(12.2)

где 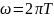– угловая скорость вращения (T - период вращения Земли); r - расстояние от точки А до оси вращения, – ли­нейная скорость на поверхности Земли. Период вращения Земли (астрономические сутки) составляет Т = 86164 с, линейная ско­рость вращения максимальна на экваторе ( = 460 м/с) и равна нулю на географических полюсах.

Рис. 12.1. Сила тяжести и сила притяжения:

а - составляющие силы тяжести; б - притягивающие массы в пространстве

В общем случае сила тяжести не направлена точно к центру Земли. Отклонение от центра зависит, во-первых, от величины центробежной силы и, во-вторых, оттого, что Земля не имеет точной сферической формы. Поскольку максимальное значение центробежной силы составляет 1/288 величины силы притяже­ния, а коэффициент сжатия Земли очень мал, отклонение на­правления силы тяжести от центра Земли не слишком велико и им часто пренебрегают.

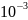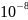Единицей измерения силы тяжести является см/с², которая называется галом в честь Галилея, впервые измерившего ускоре­ние свободного падения (1 Гал = 0,01 м/с²). В гравиразведке ис­пользуются более дробные единицы миллигал (мГал) и микро- гал (мкГал) - соответственно, и гала.

Компоненты силы притяжения и центробежной силы. Со­гласно закону Ньютона, если одну из точечных масс в точке А на поверхности земного сфероида считать единичной массой m = 1, то другая точечная масса dm, представляющая совокупность масс Земли с постоянной плотностью 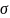, будет притягивать эту единичную массу с силой 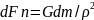, где р - расстояние между точечными массами (рис. 12.1, б). Поскольку расстояния до центров разных точечных масс dm различны, необходимо вычислить компоненты силы притяжения, создаваемые каждой из них в отдельности, используя косинусы углов между направлением

(12.3)

и осями x, y и z:

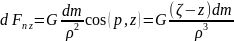(12.4)

Для вычисления компонента силы притяжения, создаваемых всей массой Земли, выражения (12.4) проинтегрируем по всему ее объему Ω:

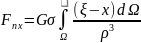
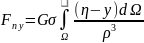
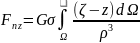(12.5)

Полное значение силы притяжения в точке А

(12.6)

Компоненты центробежной силы можно выразить так:

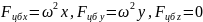(12.7)

Полное значение центробежной силы в точке А:

(12.8)

Согласно определению силы тяжести и с учетом выражений (12.5) и (12.7), составляющие силы тяжести будут равны:

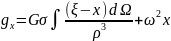
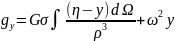
(12.9)

Полное значение силы тяжести в произвольной точке А на поверхности однородного земного сфероида

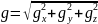(12.10)

Потенциал силы тяжести и его производные. Свойства поля силы тяжести анализируются значительно проще при переходе от векторных значений силы тяжести к скалярным. В качестве скалярной функции, определяющей поле силы тяжести, вводится функция W, называемая потенциалом силы тяжести или гра­витационным потенциалом. По физическому смыслу гравитаци­онный потенциал в некоторой точке характеризует меру энергии, которую необходимо затратить для перемещения в поле силы тяжести тела единичной массы из этой точки в бесконечность. Значение потенциала максимально в центре Земли, при удале­нии от которого потенциал непрерывно убывает.

Поверхность, вдоль которой значения потенциала постоянны, называется уровенной (эквипотенциальной) поверхностью. В любой точке уровенной поверхности сила тяжести направлена по нормали к этой поверхности, т.е.

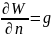(12.11)

а соответствующие производные по координатным осям равны:

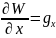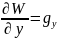, , (12.12)

Простой проверкой можно убедиться, что гравитационный по­тенциал определяется формулой

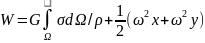(12.13)

т.е. равен сумме потенциала силы притяжения V и потенциала центробежной силы U:

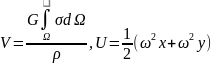(12.14)

Кроме первых производных в гравиразведке используются вторые производные потенциала силы тяжести, общее количест­во которых равно шести:

, , ,

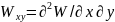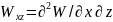, , (12.15)

В основном, в гравиразведке используются только три из этих вторых производных потенциала, которые связаны с вертикальным градиентом потенциала силы тяжести 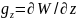, изменяющимся по координатным осям:

,

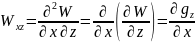, (12.16)

.

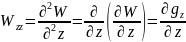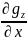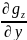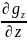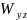Градиент характеризует скорость изменения вертикаль­ной составляющей силы тяжести по вертикали и называется вертикальным градиентом силы тяжести. Градиенты и определяют скорость изменения силы тяжести по осям х и у и называются горизонтальными градиентами силы тяже­сти. Геометрическую сумму горизонтальных градиентов и , характеризующих величину и направление максимального изменения силы тяжести в горизонтальной плоскости, называют полным горизонтальным градиентом силы тяжести:

(12.17)

Для измерения градиентов силы тяжести введена специальная единица, получившая название этвеш (Е). Один этвеш (1Е) со­ответствует изменению силы тяжести в 0,1 мГал на расстоянии 1 км.

Остальные три вторые производные потенциала силы тяжест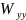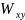и , , характеризуют форму уровенной поверхности в за­данной точке и могут быть использованы для определения кри­визны поверхности в этой точке. Измерение этих производных с помощью приборов (вариометров) позволяет установить истин­ную фигуру Земли.