2. Методические рекомендации
С учетом результатов лабораторной работы №2 продолжить работу планирования эксперимента и выполнить:
Составить уравнение регрессии общего вида для двухфакторного эксперимента;
Найти коэффициенты уравнения регрессии;
С помощью критерия Стьюдента оценить значимость коэффициентов регрессии;
Составить уравнение регрессии в кодированном виде и проверить его адекватность с помощью критерия Фишера.
Для подсчёта коэффициентов регрессии используйте формулы (3.2-3.4). Значения уi и у jm возьмите из лабораторной работы №2. Благодаря кодированию факторов расчет коэффициентов превратился в простую арифметическую процедуру. Для подсчета коэффициента b1 используется вектор-столбец Х1, а для b2 – столбец Х2.
b1= (-42+90-46+56) / 4 =14,5
b2= (-42-90+46+56) / 4 =-30
bо= (+42+90+46+56) / 4 =58,5
При вычислении коэффициента, соответствующего эффекту взаимодействия, мы обращаемся к вектор-столбцу Х1Х2.
b12 = (+42-90-46+56) / 4 = -9,5
Столбцы Х1 и Х2 задают планирование – по ним непосредственно определяются условия опытов, а столбцы Х0 и Х1Х2 служат только для расчета.
Подставим полученные коэффициенты регрессии в уравнение (3.1) и мы получим уравнение регрессии, описывающее исследуемый объект:
y = 58,5 + 14,5Х1 – 30Х2 - 9,5Х1Х2 (3.12)
После получения уравнения произвести статистический анализ значимости вычисленных коэффициентов регрессии и проверку адекватности воспроизводимости коэффициентов уравнения Sb2 по формуле (3.5). Для этого построчные дисперсии в каждом опыте плана Ŝу2 - найти из данных таблицы расчетов лабораторной работы №2.
Sb2 = (43+16+21+4) / 4 = 21
Ошибку в определении коэффициентов регрессии вычислить, извлекая корень из адекватности воспроизводимости Sb2 , откуда Sb =4,58
Коэффициенты
регрессии значимы, если
.
Вычислить доверительный интервал для коэффициентов модели, как произведение ошибки в определении коэффициентов Sb, умноженное на табличное значение критерия Стьюдента t (значение критерия Стьюдента находим по таблице приложения 2). Для доверительной вероятности Р=0,95, при числе степеней свободы f=N(т-1)=4(3-1)=8, значение критерия Стьюдента t=2,31; т – число параллельных опытов, проведенных при одинаковых условиях.
Sbt = 2,31 ·4,58 = 10,58
Для оценки значимости коэффициентов регрессии рассмотрим следующие соотношения:
=
58,5 > Sbt
;
= 14,5 > Sbt
;
= 30 > Sbt
;
= 9,5 < Sbt
;
Отсюда видно, что коэффициент регрессии b12 незначим.
Отбросим статистически незначимые коэффициенты и получим математическое описание процесса в виде линейного уравнения регрессии:
y = 58,5 + 14,5Х1 – 30Х2 (3.13)
Уравнение, включающее только оставшиеся значимые коэффициенты, проверяется на адекватность.
Полученное уравнение регрессии необходимо проверить на адекватность исследуемому объекту. Для этой цели необходимо оценить, насколько отличаются средние значения yi параметра оптимизации, полученной в точках факторного пространства от значений yi, полученных из уравнения регрессии в тех же точках факторного пространства. Для этого используем формулу дисперсии адекватности (3.9) и уравнение 3.13.
y1р = 58,5 + 14,5(-1)-30(-1)=74
y2р = 58,5 + 14,5(+1) -30(-1)=103
y3р = 58,5 + 14,5(-1) -30(+1) =14
y4р = 58,5 + 14,5(+1) -30(+1) =43
Проверку
адекватности модели осуществить с
помощью критерия Фишера по формуле
(3.10). Дисперсия воспроизводимости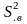
=21.
Вычислить оценку дисперсности адекватности по формуле (3.9):
1=1/(4-3)[(42-74)2+(90-103)2+(46-14)2+(56-43)2]= =1·(1024+169+1024+169)=2386
Адекватность модели проверяют по F- критерию Фишера:
Fp= S2ад/S2в. Fp = 2386/21=113,6
Найденное расчетным путем Fp сравнить с табличным значением Fтабл (см. приложение 4), которое определяется при уровне значимости a=0,05 и числе степеней свободы fад = N–В=4-3=1 и fв = N(m-1)=4(3-1)=8. Fтабл=238,88.
Если Fp< Fтабл, то полученная математическая модель с принятым уровнем статистической значимости a адекватна экспериментальным данным. В рассматриваемом примере , 113,6<238,88, следовательно, уравнение регрессии y = 58,5 + 14,5Х1 – 30Х2 является адекватным исследуемому объекту, при доверительной вероятности Р=0,95.