2. Выделение тренда с помощью скользящих и экспоненциальных средних

2.1. Сглаживание временных рядов методом простых скользящих средних

Аналитическое выравнивание уровней динамического ряда не дает хороших результатов при прогнозировании, если уровни ряда имеют резкие периодические колебания. В этих случаях для определения тенденции развития явления используется сглаживание динамического ряда методом скользящих средних.

Суть различных приемов сглаживания сводится к замене фактических уровней временного ряда расчетными уровнями, которые подвержены колебаниям в меньшей степени. Это способствует более четкому проявлению тенденции развития.

Методы сглаживания можно условно разделить на два класса, опирающиеся на различные подходы:

- аналитический подход;

- алгоритмический подход.

Аналитический подход основан на допущении, что исследователь может задать общий вид функции, описывающей регулярную, неслучайную составляющую.

При использовании алгоритмического подхода отказываются от ограничения, свойственного аналитическому. Процедуры этого класса не предполагают описание динамики неслучайной составляющей с помощью единой функции, они предполагают описание динамики неслучайной составляющей с помощью единой функции, они предоставляют исследователю лишь алгоритм расчета неслучайной составляющей в любой данный момент времени . Методы сглаживания временных рядов с помощью скользящих средних относятся к этому подходу.

Иногда скользящие средние применяют как предварительный этап перед моделированием тренда с помощью процедур, относящихся к аналитическому подходу.

Скользящие средние позволяют сгладить как случайные, так и периодические колебания, выявить имеющуюся тенденцию в развитии процесса и поэтому служат важным инструментом при фильтрации компонент временного ряда.

Алгоритм сглаживания по простой скользящей средней может быть представлен в виде следующего алгоритма.

1. Определяют длину интервала сглаживания g, включающего в себя g последовательных уровней ряда (g<n). При этом надо иметь в виду, что чем шире интервал сглаживания, тем в большей степени взаимопогашаются колебания и тенденция развития носит более плавный, сглаженный характер. Чем сильнее колебания, тем шире должен быть интервал сглаживания.

2. Разбивают весь период наблюдений на участки, при этом интервал сглаживания как бы скользит по ряду с шагом, равным 1.

3. Рассчитывают арифметические средние из уровней ряда, образующих каждый участок.

4. Заменяют фактические значения ряда, стоящие в центре каждого участка, на соответствующее среднее значение

При этом удобно брать длину интервала сглаживания g в виде нечетного числа g=2p+1, т.к. в этом случае полученные значения скользящей средней приходятся на средний член интервала.

Наблюдения, которые берутся для расчета среднего значения, называются активным участком сглаживания.

При нечетном значении g все уровни активного участка могут быть представлены в виде:

,

а скользящая средняя определяется по формуле

,

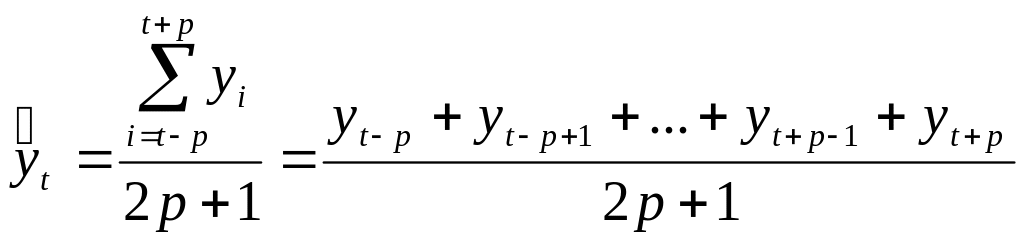где − фактические значение -го уровня;

− значение скользящей средней в момент ;

− длина интервала сглаживания.

Процедура сглаживания приводит к полному устранению периодических колебаний во временном ряду, если длина интервала сглаживания берется равной или кратной периоду колебаний.

Для устранения сезонных колебаний желательно использовать четырех- и двенадцатичленную скользящую среднюю.

При четном числе уровней принято первое и последнее наблюдение на активном участке брать с половинными весами:

.

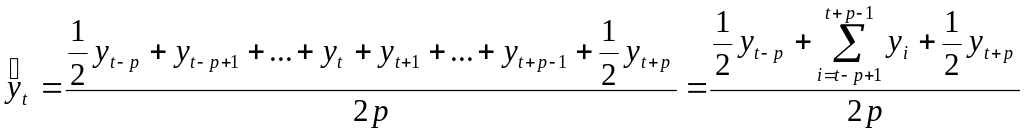Тогда для сглаживания колебаний при работе с временными рядами квартальной или месячной динамики можно использовать следующие скользящие средние:

,

.

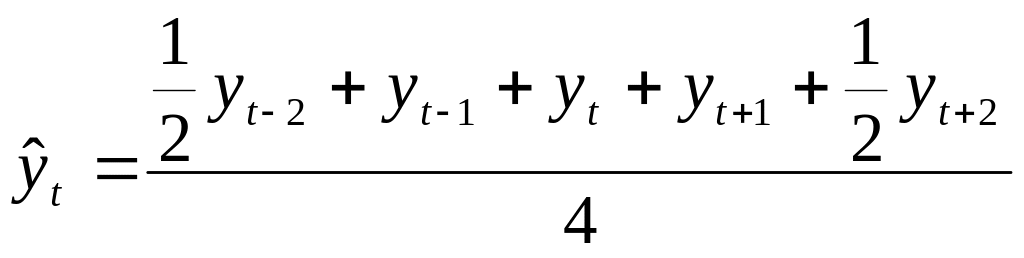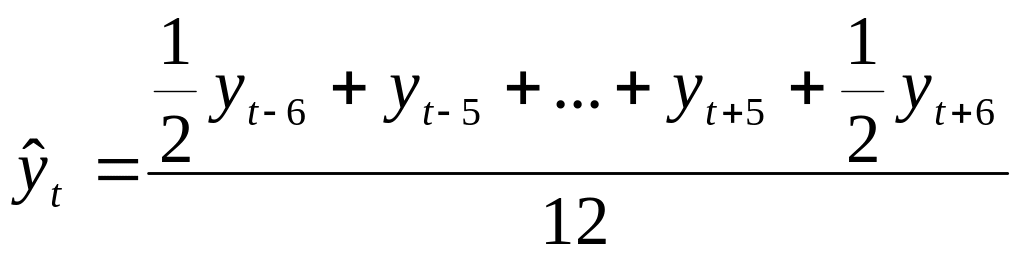Рассмотрим применение скользящей средней по данным общей площади жилых помещений, приходящихся в среднем на 1 жителя по Хабаровскому краю (таблица 2.1.1).

Поскольку период сглаживания не обосновать, расчеты начинают с 3-членной скользящей средней. Первый сглаженный уровень получим для 1993 г.:

.

Последовательно сдвигая на один год начало периода скольжения, находим сглаженные уровни для последующих лет.

Для 1994 г. скользящая средняя составит

,

для 1995 г. , и т.д.

Так как скользящая средняя относится к середине интервала, за который она рассчитана, то динамический ряд сглаженных уровней сокращается на уровень при нечетном периоде скольжения и на уровней при четном периоде скольжения. Поэтому в нашем примере сглаженный ряд стал короче на два члена для трехчленной средней и на четыре – для пятичленной (таблица 2.1.1).

При расчете по четным скользящим средним (в нашем примере 4-членная скользящая средняя) вычисления производятся следующим образом:

Для 1994 г. ;

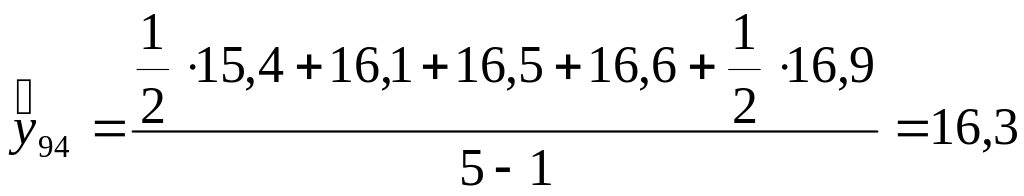1995 г. ;

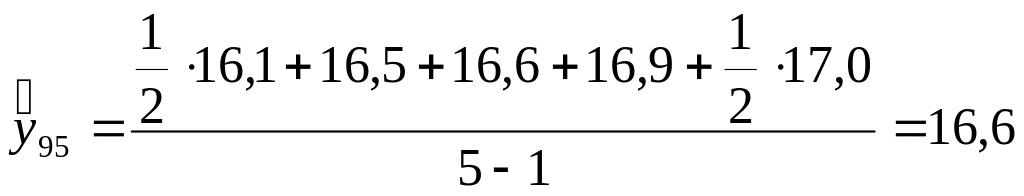1996 г. .

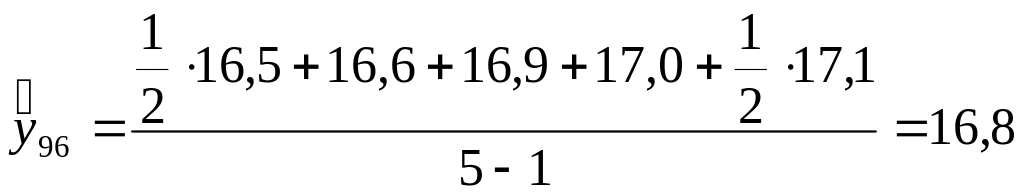Таблица 2.1.1 – Результаты сглаживания по методу скользящих средних

Годы	Общая пло-щадь жилых помещений, приходящаяся в среднем на 1 жителя.кв.м,	Сглаженные уровни
		Простая скользящая средняя
		3-член-ная,	4-член-ная,	5-член-ная,		3-член-ная	4-член-ная	5-член-ная
1992	15,4	-	-	-		-	-	-
1993	16,1	16,0	-	-		0,01	-	-
1994	16,5	16,4	16,3	16,3		0,01	0,026	0,040
1995	16,6	16,7	16,6	16,6		0,004	0,001	0,000
1996	16,9	16,8	16,8	16,8		0,004	0,006	0,006
1997	17,0	17,0	17,1	17,1		0	0,003	0,010
1998	17,1	17,3	17,4	17,4		0,05	0,083	0,102
1999	17,9	17,7	17,7	17,7		0,03	0,026	0,026
2000	18,2	18,2	18,2	18,2		0,00	0,000	0,000
2001	18,5	18,7	18,7	18,7		0,03	0,031	0,032
2002	19,3	19,1	19.1	19,0		0,04	0,056	0,068
2003	19,5	19,5	19,4	19,4		0	0,006	0,014
2004	19,7	19,7	-	-		0	-	-
2005	19,9	-	-	-		-	-	-
Итого	248,6	-	-	-		0,179	0,239	0,299

Как видно из таблицы 2.1.1, трехчленная скользящая средняя демонстрирует выравненный динамический ряд с однонаправленной тенденцией движения уровней. Сглаживание по трехчленной скользящей средней дало более сглаженный ряд, так как для трехчленной скользящей средней оказалась меньше сумма квадратов отклонений фактических данных ( ) от сглаженных ( ) ( = 0,179) (таблица 2.1.1). Иными словами, трехчленная скользящая средняя лучше всего представляет закономерность движения уровней динамического ряда.