1 Билет

1. Определение геометрического ряда. Теорема (необходимый признак сходимости). Теорема (о погружении дискретного аргумента (n) в непрерывный (X).

Опр1. Геометрическим рядом называется ряд, составленный из членов геометрической прогрессии.

a+aq+aq^2+…+aq^(n-1)+…=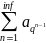 , где a≠0

Теорема1. Необх. призн сх-ти.

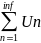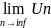Если ряд – сходится, то его общий член стремится к 0, т.е. =0

Следствие. Если общий член ряда не стремится к 0, при

n→бесконечности, т.е. ≠0, то ряд расходится.

Теорема2. о погруж. дискр. арг-та n в непрерывный х.

Если 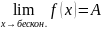и при этом существует, то 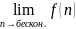также существует и равен А.

2. Определение функции нескольких переменных. Определение множества значений фнп. Определение графика функции. Определение линии уровня.

Опр1. Пусть имеется n переменных величин и каждому набору их значений (х1,х2,…,хn) из некоторого мн-ва Х соответствует одно вполне определенное значение переменной величины z. Тогда говорят, что задана ф-ия нескольких переменных z=f(x1,x2,…,xn). При этом переменные x1,x2,…,xn называются независимыми переменными или аргументами, z-зависимой переменной, f – закон соответствия, Х- областью опр ф-ии и обозн D(z).

Опр2. Совокупность всех значений функции z=f(x,y) называется множеством ее значений и обозначается символом E(z)

Опр3.Графиком ф-и z=f(x,y) наз-ся множество G(z)={(x,y,z)εR³|z=f(x,y),(x,y)εD(z)} Графиком ф-ии z=f(x,y) представляет собой некоторую поверхность в трехмерном пространстве.

Опр4. Линией уровня функции z=f(x,y) называется множество точек на плоскости, в которых ф-ия принимает одно и то же значение С. Число С в этом случае называется уровнем

3 Билет

1) 1 признак сравнения + эталонные ряды;

Т: (1-й признак сравн) Пусть даны 2 рада с положительными членами Ʃun и Ʃvn, каждый член 1го ряда не превосходит соответствующего члена 2го ряда, те un≤vn(n=1,2…)Тогда: 1) если сходится ряд Ʃvn, то сходится и Ʃun 2) если расходится Ʃun, то расходится и ряд Ʃvn

Эталонные ряды:

1) геометрический ряд: Ʃaq^n-1 j сходится при │q│˂1 и расходится при│q│ ≥1

2) гармонический ряд Ʃ1/n j расходится

3) обобщенный гармонический ряд (Дерихле) Ʃ 1/n^p j сход при p˃1 и расх при р≤1.

2) Определение ду, обыкновенное и ду в частных производных, порядок и решение;

О: Дифференциальным уравнением называется уравнение, связывающее независимые переменные функции и её производные.

О: Если независимая переменная одна, то уравнение называется обыкновенным, а если независимых переменных 2 или более, то уравнение называется ДУ в частных произв-ых.

О: Порядком ДУ называется порядок наивысшей производной, входящей в уравнение.

О: Решением ДУ называется любая функция, которая при подстановке в уравнение обращает его в тождество.

3) (1-2y)xdx+(1+x^2)dy=0

4 Билет

1.Второй предельный признак сравнения. Признак Даламбера

Теорема: (2-й (предельный) признак сравнения) Если Ʃun и Ʃvn ряды с положительными членами и существует конечный предел отношения их общих членов lim un/vn=k≠0, то ряды одновременно сходятся, либо одновременно расходятся.

Теорема: (признак Даламбера) Если дан ряд Ʃun с положительными членами и существует предел lim u(n+1)/un=D, тогда

1) ряд сходится, если D˂1

2) ряд расходится, если D˃1

Замечание: если D=1 – ряд может как сходится, так и расходится. Необходимо дополнительное исследование ряда с помощью других признаков. 2.Уравнение в полных дифференциалах 

Определение: Уравнение вида M(x,y)dx+N(x,y)dy=0 (2) называется уравнение в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции F(х,у), те dF(x,y)=∂F/∂x*dx+∂F/∂y*dy≡M(x,y)dx+N(x,y)dy

Теорема: Для того, чтобы уравнение (2) было уравнением в полных дифференциалах необходимо и достаточно, чтобы ∂ M(x,y)/∂у≡∂N(x,y)/∂х

Метод решения уравнений в полных дифференциалах, т.е. уравнения (2) основан на нахождении функции F(х,у), от которой полный дифференциал равен явной части данного уравнения. Тогда общее решение уравнения (2) можно записать в виде F(x,у)=С.

Замечание: Искомая функция F(x,у) находится из системы уравнений:

∂F(x,у)/∂х=М(х,у)

∂F(x,у)/∂у=N(х,у)

Находим функцию F(x,y).

F(х,у)=∫M(х,у)dx=Ф(x,y)+g(y).

Дифференцируя полученную функцию по у с учетом 2го уравнения получаем уравнение для определения функции g(y):

∂Ф(х,у)/∂у+∂g(y)/∂y=N(x,y)

Билет 5.