- •К.П. Лихоеденко, ю.А. Сидоркина, в.Ю. Цыганков Свойства p-n перехода. Полупроводниковые диоды.
- •Оглавление
- •Введение
- •Методические рекомендации
- •Часть1. Семинарские занятия
- •1.1. Основные свойства р-nперехода
- •1.2. Полупроводниковые диоды
- •1.3 Стабилитроны
- •Часть 2. Варианты домашнего задания
- •Вопросы для подготовки к защите дз [1-4,6-8]
- •Список литературы
- •Свойства p-n перехода. Полупроводниковые диоды
1.2. Полупроводниковые диоды
Основой полупроводниковых диодов служит р-n переход. Поэтому свойства диода и вольт-амперная (ВАХ) характеристика отражают особенности прохождения тока через р-n переход.
Выражение (1.8) описывает ВАХ идеального р-n перехода. ВАХ реальных кремниевых диодов отличаются от характеристик идеального перехода. Типичная ВАХ кремниевого диода представлена на рис. 1.2.
Характерная
особенность ВАХ реальных диодов -
отсутствие на рисунках токов через диод
при отрицательных и малых положительных
напряжениях, т.е. при
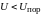 ,
(см. рис, 1.2). Обратные токи в диодах малы,
поэтому в инженерных расчетах их полагают
равными нулю; заметный ток появляется
только при
,
(см. рис, 1.2). Обратные токи в диодах малы,
поэтому в инженерных расчетах их полагают
равными нулю; заметный ток появляется
только при
 .
Область напряжений
.
Область напряжений
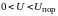 называется зоной умолчания. Иногда при
анализе кремнистых интегральных схем
ВАХ диода изображают в виде ступеньки
(рис. 1.3), то есть представляют диод в
виде идеальною ключа.
называется зоной умолчания. Иногда при
анализе кремнистых интегральных схем
ВАХ диода изображают в виде ступеньки
(рис. 1.3), то есть представляют диод в
виде идеальною ключа.
К
основным параметрам диода относятся
сопротивление диода постоянному току
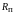 и дифференциальное сопротивление
и дифференциальное сопротивление
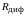 .
Величина
определяется как отношение постоянного
напряжения на диоде к току через него.
Дифференциальное сопротивление
характеризует наклон к оси абсцисс
вольт-амперной характеристики при
данном напряжении на диоде:
.
Величина
определяется как отношение постоянного
напряжения на диоде к току через него.
Дифференциальное сопротивление
характеризует наклон к оси абсцисс
вольт-амперной характеристики при
данном напряжении на диоде: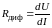 .
.
|
|
Рис. 1.2. Вольт-амперная характеристика кремниевого диода |
Рис. 1.3. Вольт-амперная характеристика идеального ключа |
Отличие характеристик реальных диодов от ВАХ идеального р-n перехода делает практически невозможным аналитический расчет токов и напряжении в реальных схемах с диодами. Поэтому на практике пользуются графоаналитическим методом решения задач. При этом используют реальные характеристики диодов, например приведенные в справочниках. Суть этого метода поясним на простом примере.
Пример 1.8.
Определить
ток
текущий в схеме, представленной на рис.
1.4. Известна ВАХ диода (рис. 1.5),
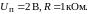
Для решения запишем 2-ой закон Кирхгофа для цепи (рис. 1.4):
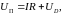 (1.20)
(1.20)
где
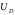 - падение напряжения на диоде.
- падение напряжения на диоде.
|
|
Рис. 1.4. Схема включения диода |
Рис. 1.5. Иллюстрация графического метода определения тока через диод и напряжение на нем |
Это
уравнение содержит две неизвестные
величины: I
и
.
Чтобы их определить,
нужно еще одно уравнение. Его роль
выполняет ВАХ диода, дающая
связь между I
и
.
Учитывая, что (1.20) - это уравнение прямой,
задачу
удобно решить графически. Построим
нагрузочную прямую (1.20) по
двум точкам (точкам ее пересечения с
осями координат). Напряжение холостого
хода
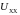 -
это точка пересечения нагрузочной
прямой с осью абсцисс;
-
это точка пересечения нагрузочной
прямой с осью абсцисс;
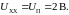 .
Ток короткого замыкания
.
Ток короткого замыкания
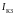 -
точка пересечения прямой
с осью ординат;
-
точка пересечения прямой
с осью ординат;
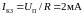 .
Точка пересечения прямой с
характеристикой дает искомое решение
задачи:
.
Точка пересечения прямой с
характеристикой дает искомое решение
задачи:
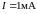 ;
;
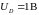 .
.
Пример 1.9.
В
схеме, изображенной на рис. 1.6,
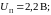
 ВАХ
диодов
приведена на рис. 1.7. Определить токи
через диоды и напряжение на
выходе
ВАХ
диодов
приведена на рис. 1.7. Определить токи
через диоды и напряжение на
выходе
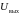 .
Определить
дифференциальное сопротивление диодов
.
Определить
дифференциальное сопротивление диодов
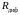 и
сопротивление по постоянному току
и
сопротивление по постоянному току
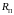 .
.
|
|
Рис. 1.6. Схема включения диодов |
Рис. 1.7. Вольт-амперная характеристика диода |
Решение:
Поскольку напряжения
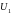 и
и
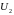 —
одинаковые, то напряжения
на диодах
—
одинаковые, то напряжения
на диодах
 и
и
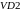 и
токи через эти диоды одинаковы. Обозначим
их
через
и
и
токи через эти диоды одинаковы. Обозначим
их
через
и
 соответственно. Предположим, что диод
соответственно. Предположим, что диод
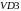 открыт, т. е. ток через этот диод отличен
от нуля. Из рис. 1.7 видно, что это возможно,
если
потенциал точки А (рис. 1.6) превышает
величину
открыт, т. е. ток через этот диод отличен
от нуля. Из рис. 1.7 видно, что это возможно,
если
потенциал точки А (рис. 1.6) превышает
величину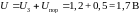 .
Здесь через
.
Здесь через
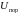 обозначено пороговое напряжение диода,
отвечающее границе «зоны умолчания»
на вольт-амперной характеристике.
Если это так, то напряжение на диодах
и
окажется равным
обозначено пороговое напряжение диода,
отвечающее границе «зоны умолчания»
на вольт-амперной характеристике.
Если это так, то напряжение на диодах
и
окажется равным
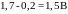 ,
что противоречит рис. 1.7. Потому при
решении
задачи будем считать, что диод
закрыт, т. е. ток через него не течет. Ток
I
через сопротивление R
в
соответствии с 1-м законом Кирхгофа
равен
удвоенному току через открытый диод:
,
что противоречит рис. 1.7. Потому при
решении
задачи будем считать, что диод
закрыт, т. е. ток через него не течет. Ток
I
через сопротивление R
в
соответствии с 1-м законом Кирхгофа
равен
удвоенному току через открытый диод: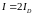 .
Согласно
2-му закону Кирхгофа
.
Согласно
2-му закону Кирхгофа
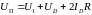 (1.21)
(1.21)
Уравнение
(1.21)
содержит две неизвестные величины:
и
.Чтобы
их определить, необходимо еще одно
уравнение, в данном случае второе
уравнение задано графически в виде ВАХ
диода. Уравнение (1.21) представляет собой
уравнение нагрузочной прямой. Чтобы
построить эту
прямую
в плоскости вольт-амперной характеристики
(ВАХ) диода, нужно
определить точки пересечения этой
характеристики с осями координат.
Положив
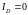 ,
получим точку пересечения прямой с осью
напряжений
(напряжение холостого хода):
,
получим точку пересечения прямой с осью
напряжений
(напряжение холостого хода):
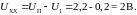
Положив
далее
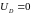 ,
получим
точку пересечения нагрузочной прямой
с осью ординат -
(ток короткого замыкания):
,
получим
точку пересечения нагрузочной прямой
с осью ординат -
(ток короткого замыкания):

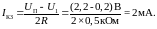
Поскольку
значение
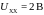 не
помешается на графике рис. 1.7, построим
сначала вспомогательную прямую,
параллельную нагрузочной прямой.
Пусть вспомогательная прямая пересекает
ось напряжений в точке
не
помешается на графике рис. 1.7, построим
сначала вспомогательную прямую,
параллельную нагрузочной прямой.
Пусть вспомогательная прямая пересекает
ось напряжений в точке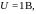 т.е.
т.е.
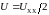 ;
тогда эта прямая должна пересечь ось
ординат (токов)
в точке
;
тогда эта прямая должна пересечь ось
ординат (токов)
в точке
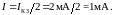 Проведем вспомогательную прямую
через точки (0; 1 мА) и (1 В; 0) на
графике рис. 1.7.
Нагрузочная
прямая
пройдет через точку (0; 2 мА)
параллельно вспомогательной.
Проведем вспомогательную прямую
через точки (0; 1 мА) и (1 В; 0) на
графике рис. 1.7.
Нагрузочная
прямая
пройдет через точку (0; 2 мА)
параллельно вспомогательной.
Отметим, что прямая (1.21), вообще говоря, может быть построена в плоскости (U, I) по любым двум точкам; описанный выше способ построения этой прямой - один из возможных.
По
точке пересечения нагрузочной прямой
и ВАХ диода определяется ток
через открытые диоды
и напряжение
на этих диодах
: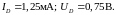
Напряжение
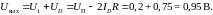
Диод
в
этом случае закрыт, как и полагалось
ранее; напряжение на нем
равно
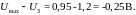
Сопротивление постоянному току равно
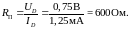
Чтобы
определить дифференциальное сопротивление,
нужно провести касательную к ВАХ в
рабочей точке и построить прямоугольный
треугольник, гипотенуза которого - часть
касательной, а катеты параллельны осям.
Отношение катетов
 равно дифференциальному сопротивлению.
Пользуясь построением на рис. 1.7,
определим:
равно дифференциальному сопротивлению.
Пользуясь построением на рис. 1.7,
определим:

Ответ:
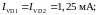
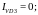

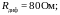
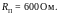
Пример 1.10
В
схеме, изображенной на рис. 1.8,
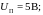
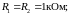
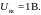 Определить токи через диоды,
напряжение на диодах и напряжение на
выходе
.Определить
дифференциальное сопротивление диодов
и сопротивление по постоянному току
Определить токи через диоды,
напряжение на диодах и напряжение на
выходе
.Определить
дифференциальное сопротивление диодов
и сопротивление по постоянному току
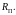 Вольт-амперная
характеристика
диодов
изображена на рис. 1.7.
Вольт-амперная
характеристика
диодов
изображена на рис. 1.7.
Решение: Согласно законам Кирхгофа токи и напряжения (рис. 1.8), связаны уравнениями
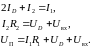
Исключая
токи
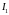 и
и
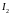 ,
получи
уравнение нагрузочной прямой в виде
,
получи
уравнение нагрузочной прямой в виде
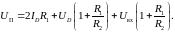
|
Рис. 1.8. Схема включения диодов |
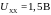 ;
полагая далее
;
полагая далее
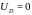 ,
получим
,
получим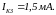 После
построения нагрузочной прямой находим
графическое решение:
После
построения нагрузочной прямой находим
графическое решение:
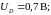
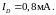 Далее, используя приведенные выше
уравнения,
можно найти все токи и напряжения в
схеме:
Далее, используя приведенные выше
уравнения,
можно найти все токи и напряжения в
схеме:
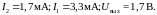 Сопротивление
диода по постоянному току и
дифференциальное
сопротивление определяются аналогично
задаче 1.10.
Сопротивление
диода по постоянному току и
дифференциальное
сопротивление определяются аналогично
задаче 1.10.
Ответ:
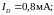
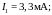
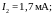
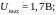
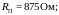
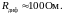
Пример 1.11.
Определить
токи
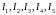 в
схеме, изображенной на
рис. 1.9.
Диоды
в
схеме, изображенной на
рис. 1.9.
Диоды
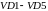 одинаковые,
их вольт-амперная характеристика
приведена на рис. 1.10.
одинаковые,
их вольт-амперная характеристика
приведена на рис. 1.10.
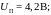
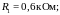
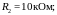
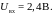
Решение: Сначала определим, по каким ветвям протекает ток, а по каким он протекать не может. Для этого оценим потенциал в точке А.
Допустим,
что ток
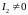 ,
т.е. через левую ветвь протекает отличный
от
нуля ток. В этом случае потенциал точки
А должен быть не менее, чем
,
т.е. через левую ветвь протекает отличный
от
нуля ток. В этом случае потенциал точки
А должен быть не менее, чем
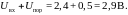
Здесь
-
пороговое напряжение включения диода,
равное 0,5 В. Однако, потенциал 2,9 В
в
точке А установиться не может, т.к.
напряжения
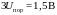 будет
достаточно, чтобы открыть диоды
будет
достаточно, чтобы открыть диоды
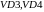 и
и
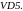 При
открытых диодах
При
открытых диодах
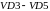 значение
напряжения в точке А лежит в
диапазоне от 1,5 В
до
значение
напряжения в точке А лежит в
диапазоне от 1,5 В
до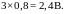 Таким образом следует ожидать, что диоды
будут
открыты, а диод
- закрыт,
и ток
окажется
Таким образом следует ожидать, что диоды
будут
открыты, а диод
- закрыт,
и ток
окажется
|
|
Рис. 1.9. Схема включения диодов |
Рис. 1.10. Вольт-амперная характеристика диода |
равным
нулю. Токи через диоды
и
одинаковы:
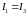 .
Ток
.
Ток
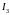 разветвляется
в точке В: ток через сопротивление
разветвляется
в точке В: ток через сопротивление
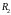 -
-
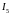 и
ток через диоды
и
ток через диоды
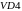 и
и
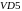 -
-
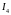 .
В данной задаче найти решение методом
нагрузочной прямой
удается, если через все диоды течет
одинаковый ток. Однако, ток
больше
тока
на величину тока
.Задачу
можно решить приближенно, если
.
В данной задаче найти решение методом
нагрузочной прямой
удается, если через все диоды течет
одинаковый ток. Однако, ток
больше
тока
на величину тока
.Задачу
можно решить приближенно, если
 .
Оценим
эти токи. Потенциал точки В при открытых
диодах
.
Оценим
эти токи. Потенциал точки В при открытых
диодах
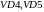 может
принимать значения от
может
принимать значения от
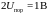 до
до
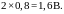 Следовательно,
не
превышает величины
Следовательно,
не
превышает величины
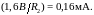 С
другой стороны,
ток
(и равный ему
)
не могут быть меньше значения
С
другой стороны,
ток
(и равный ему
)
не могут быть меньше значения
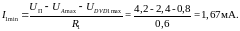
Поскольку
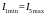 ,
можно сделать вывод, что при решении
задачи
графоаналитическим методом током
можно пренебречь, и считать, что
через диоды
,
можно сделать вывод, что при решении
задачи
графоаналитическим методом током
можно пренебречь, и считать, что
через диоды
 и
течет
одинаковый ток
и, следовательно,
падение напряжения на этих диодах тоже
одинаково. Считая
и
течет
одинаковый ток
и, следовательно,
падение напряжения на этих диодах тоже
одинаково. Считая
 ,
запишем
уравнение Кирхгофа для цепи
,
запишем
уравнение Кирхгофа для цепи
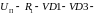
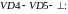
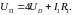
Последнее уравнение представляет собой уравнение нагрузочной прямой.
Находим
напряжение холостого хода
и ток короткого замыкания
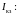
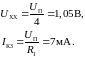
Нагрузочная
прямая (см. рис. 1.10)
пересекает ВАХ диода в точке
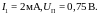 Таким
образом,
Таким
образом,
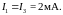 Потенциалы точек А и
В равны соответственно
Потенциалы точек А и
В равны соответственно
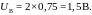 Ток
через
сопротивление
равен
Ток
через
сопротивление
равен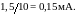 Ток
теперь можно уточнить:
Ток
теперь можно уточнить:
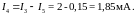
Полученное решение - приближенное, его можно уточнить методом итераций, однако в этом нет необходимости, т.к. в реальных схемах номинальные значении сопротивлений, напряжений источников питания и вольт-амперные характеристики диодов определяются (как правило) с точностью, не превышающей 5%.
Ответ:
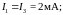
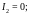
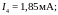
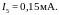
|
Рис. 1.11. Схема включения диодов |
Определить
токи
в схеме, изображенной
на рис. 1.11, если падение напряжения на
открытом
диоде равно 0,8 В.
Диоды
 одинаковые.
одинаковые.
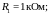
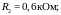
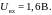
Решение:
Предположим, что ток
.
Тогда
потенциал в точке разветвления
будет равен
Предположим,
что ток
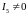 .
В этом случае потенциал точки
разветвления равен
.
В этом случае потенциал точки
разветвления равен
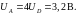 На основании этих оценок можно
сделать вывод, что либо потенциал
точки А действительно равен 3,2 В и тогда
открыты все ветви (все токи
отличны от нуля), либо в действительности
потенциал
На основании этих оценок можно
сделать вывод, что либо потенциал
точки А действительно равен 3,2 В и тогда
открыты все ветви (все токи
отличны от нуля), либо в действительности
потенциал
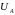 окажется
ниже
3,2 В, что означает, что ток течет по одной
единственной ветви:
окажется
ниже
3,2 В, что означает, что ток течет по одной
единственной ветви:
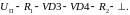 Чтобы
выяснить, какой из этих случаев
реализуется, оценим токи через
сопротивления в предположении, что
Чтобы
выяснить, какой из этих случаев
реализуется, оценим токи через
сопротивления в предположении, что
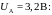
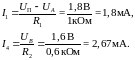
Однако
согласно схеме, изображенной на рис.
1.11, ток
не может быть больше
тока
.
Это
противоречит первому закону Кирхгофа
для узлов А и
В. Отсюда можно сделать вывод, что
предположение о том, что
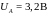 ,
неверно. На самом деле потенциал точки
А окажется ниже 3,2 В, что
означает, что
,
неверно. На самом деле потенциал точки
А окажется ниже 3,2 В, что
означает, что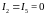 .
Далее запишем
второй закон Кирхгофа для контура
.
Далее запишем
второй закон Кирхгофа для контура
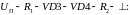

Здесь
принято во внимание, что
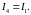 Ток
равен
Ток
равен
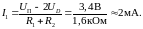
Ответ: