
- •Предисловие
- •Лабораторная работа №1 операции над множествами
- •Теоретические сведения
- •Пример выполнения работы.
- •Примеры записи нечеткого множества
- •Пример выполнения работы.
- •Контрольные вопросы
- •Задание для лабораторной работы.
- •Лабораторная работа № 3 комбинаторные алгоритмы
- •Теоретические сведения
- •Технология выполнения работы.
- •Контрольные вопросы
- •Задание для лабораторной работы.
- •Технология выполнения работы.
- •Контрольные вопросы
- •Задание для лабораторной работы.
- •Лабораторная работа №5 бинарные отношения
- •Теоретические сведения
- •Технология выполнения работы.
- •Контрольные вопросы
- •Задание для лабораторной работы.
- •Лабораторная работа № 6 Машинное представление графа
- •Теоретические сведения
- •Технология выполнения работы.
- •Контрольные вопросы
- •Задание для лабораторной работы.
- •Лабораторная работа №7 алгоритмы построения кратчайших путей в графе и кратчайшего остова графа
- •Теоретические сведения
- •Пример выполнения работы.
- •Контрольные вопросы
- •Задание для лабораторной работы.
- •Лабораторная работа №8 алгоритмы построения эйлерова и гамильтонова цикла
- •Теоретические сведения
- •Пример выполнения работы.
- •Контрольные вопросы
- •Задание для лабораторной работы.
- •Приложения
- •Варианты заданий
- •Варианты заданий
- •Варианты заданий
- •Библиографический список
- •ТеОретИческие основы информационных технологий лабораторный практикум
- •394036, Воронеж, пр. Революции, 19
Пример выполнения работы.
1. Определить нечёткое множество «молодые люди».
Решение.
В
качестве характеристического параметра
человека x
будем рассматривать его возраст
![]() ,
,
![]() .
Всюду в дальнейшем для краткости записи
формул через x
будем обозначать его характеристический
параметр
.
.
Всюду в дальнейшем для краткости записи
формул через x
будем обозначать его характеристический
параметр
.
Определим интервал, на котором
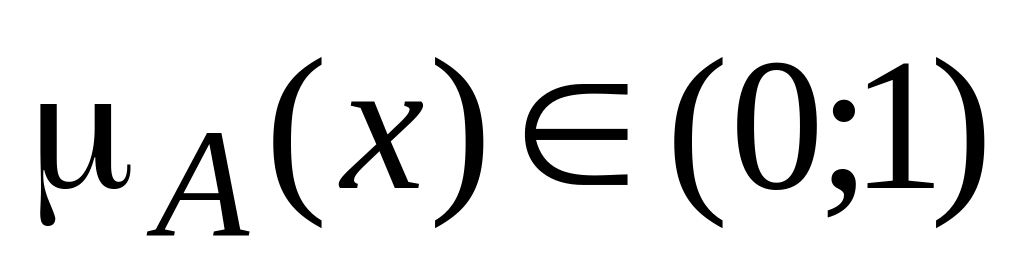 .
Положим, что если
.
Положим, что если
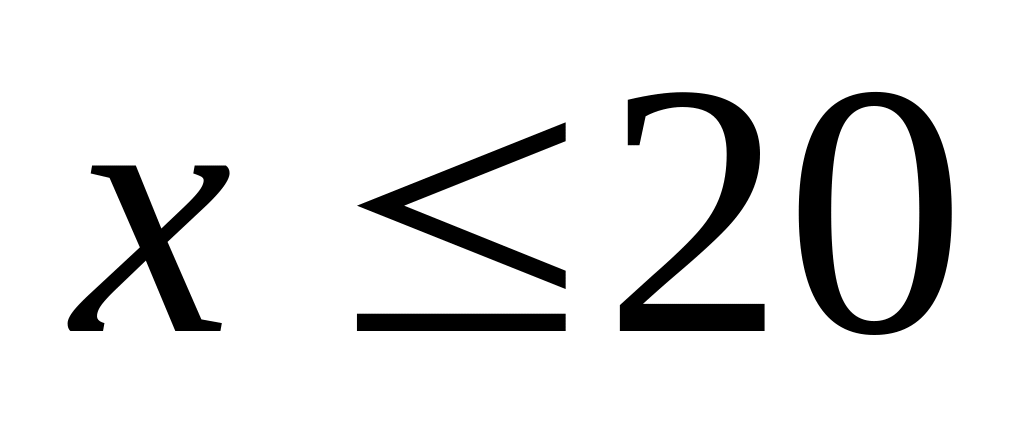 ,
то
,
то
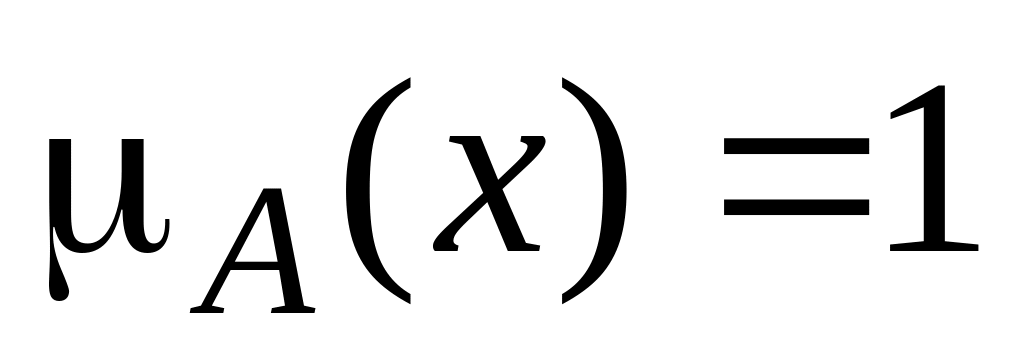 ,
а если
,
а если
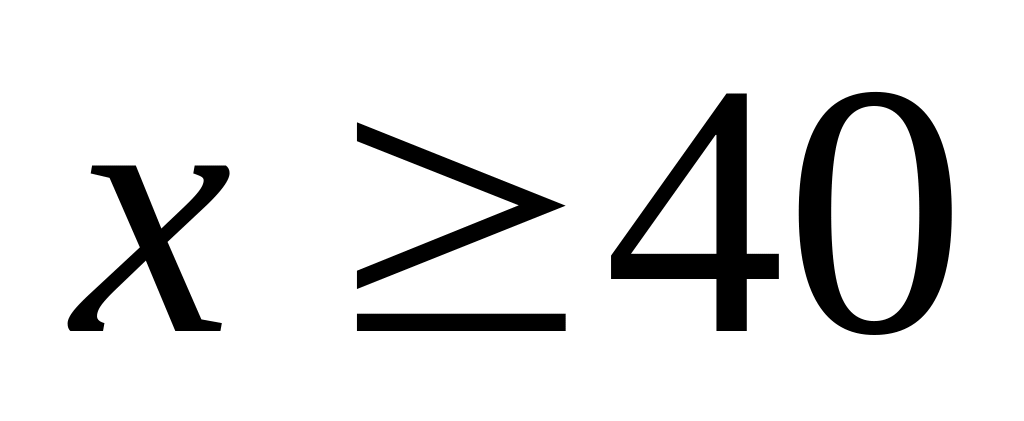 ,
то
,
то
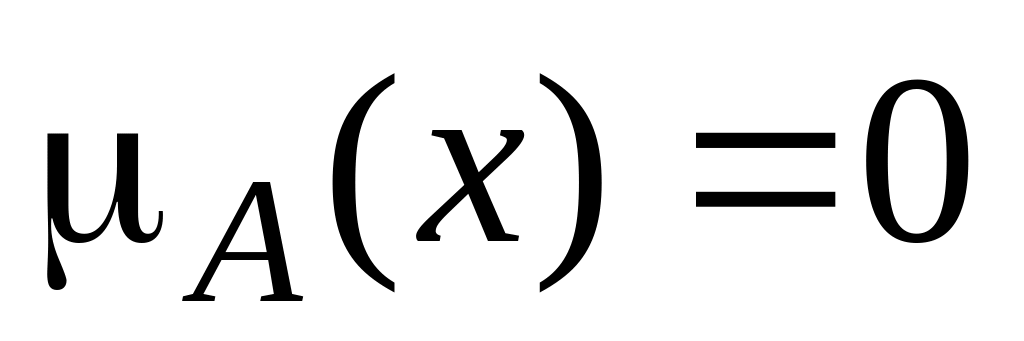 .
Следовательно, если
.
Следовательно, если
 ,
то
.
Для построения функции принадлежности
,
то
.
Для построения функции принадлежности
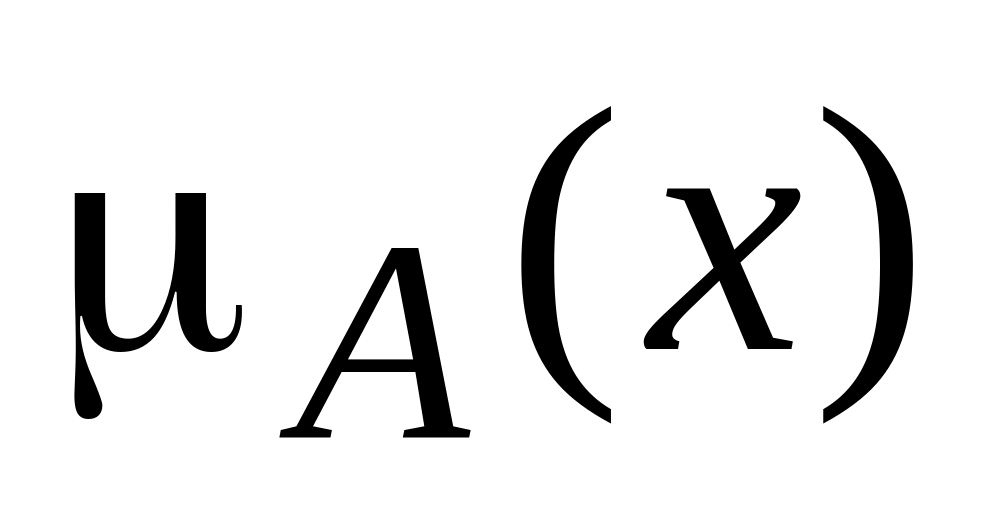 зададим значения степени принадлежности
элементов в конечном множестве точек.
Для этого разобьём интервал
зададим значения степени принадлежности
элементов в конечном множестве точек.
Для этого разобьём интервал
 на n равных частей
(например, пусть
на n равных частей
(например, пусть
 ,
тогда
,
тогда
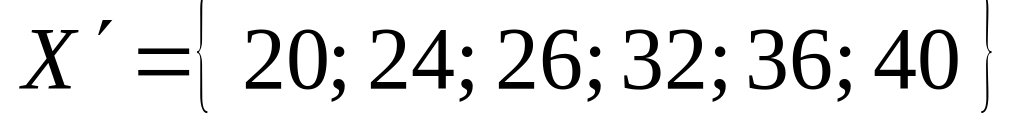 ).
Выступим в роли экспертов и зададим во
внутренних точках разбиения степени
принадлежности элемента нечёткому
множеству «молодые люди».
).
Выступим в роли экспертов и зададим во
внутренних точках разбиения степени
принадлежности элемента нечёткому
множеству «молодые люди».
|
20 |
24 |
28 |
32 |
36 |
40 |
|
1 |
0,9 |
0,7 |
0,4 |
0,1 |
0 |
Построим аппроксимацию функции . При её построении будем использовать элементарные кривые. Например, через первые и последние 3 точки проведём параболы, а 2 средние точки (28; 0,7) и (32; 0,4) соединим прямой.
Определим
коэффициенты параболы
![]() ,
проходящей через точки (20; 1), (24; 0,9), (28;
0,7). Решив систему
,
проходящей через точки (20; 1), (24; 0,9), (28;
0,7). Решив систему
линейных уравнений
 ,
(*)
,
(*)
получим
![]() .
.
Прямая,
проходящая через точки (28; 0,7) и (32; 0,4),
задаётся формулой
![]() .
.
Коэффициенты
параболы
![]() ,
проходящей через точки (32; 0,4), (36; 0,1), (40;
0), можно определить, решив аналогичную
(8) систему линейных уравнений. В этом
случае получим
,
проходящей через точки (32; 0,4), (36; 0,1), (40;
0), можно определить, решив аналогичную
(8) систему линейных уравнений. В этом
случае получим
![]() .
Однако, нетрудно за-метить, что вершина
данной параболы находится в точке (40;
0), поэтому она имеет вид
.
Однако, нетрудно за-метить, что вершина
данной параболы находится в точке (40;
0), поэтому она имеет вид
![]() .
Подставив в уравнение значения двух
других точек и решив полученную систему
уравнений, определим неизвестные
параметры
.
Подставив в уравнение значения двух
других точек и решив полученную систему
уравнений, определим неизвестные
параметры
![]() .
.
Таким образом,
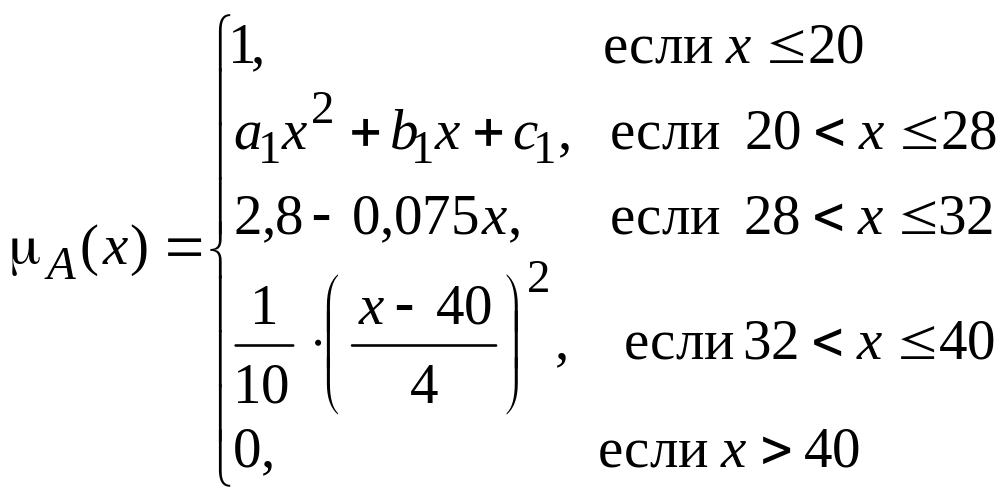 .
.
Построим график данной функции

Дано множество марок автомобилей X = {Жигули; Волга; Мерседес; Феррари; Ягуар}. Построить матрицу парных сравнений для нечёткого множества A = «скоростной автомобиль».
Решение.
Построим
матрицу парных сравнений для определения
значений функции принадлежности
![]() в конечном множестве точек
в конечном множестве точек
![]() косвенным методом. Так как автомобили
каждой последующей марки имеют более
высокие скоростные качества, то элементы
матрицы
косвенным методом. Так как автомобили
каждой последующей марки имеют более
высокие скоростные качества, то элементы
матрицы
![]() ,
находящиеся ниже главной диагонали,
превосходят 1. Степень превосходства
каждой последующей марки оценим, выступив
в качестве эксперта. Элемент, находящийся
выше главной диагонали, согласно
свойствам матрицы парных сравнений
определяется как обратный симметричному
элементу.
,
находящиеся ниже главной диагонали,
превосходят 1. Степень превосходства
каждой последующей марки оценим, выступив
в качестве эксперта. Элемент, находящийся
выше главной диагонали, согласно
свойствам матрицы парных сравнений
определяется как обратный симметричному
элементу.

Данная матрица не является идеально согласованной.
3. Даны множества:
Множество |
Степень принадлежности элемента |
||||
x1 |
x2 |
x3 |
x4 |
x5 |
|
A |
1/2 |
1/5 |
2/3 |
2/5 |
1 |
B |
1/4 |
1 |
3/5 |
7/8 |
0 |
C |
0.2 |
0.6 |
2/7 |
1/3 |
0.4 |
Найти:
 ;
;
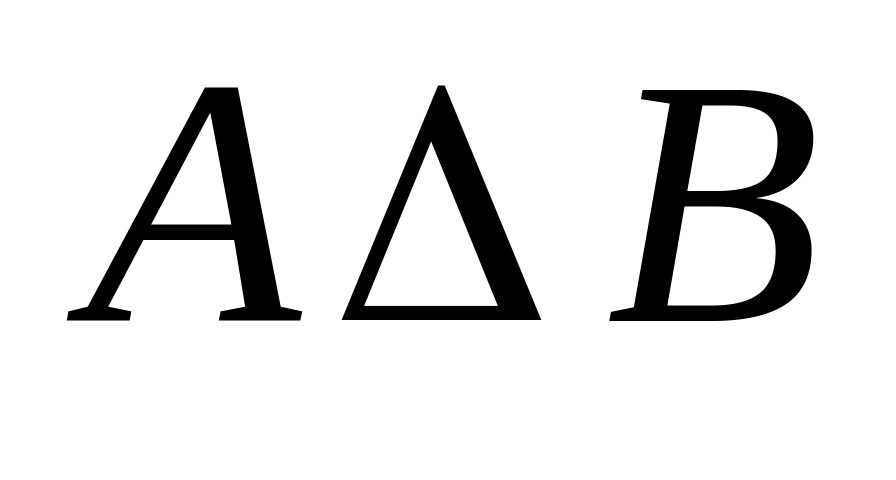 .
.
Решение.
Так как
 ,
то
,
то
![]()
![]()
![]()
![]()
![]()
![]()
![]()
