Пример выполнения работы.

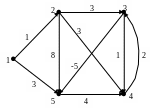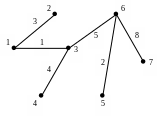
1 . Рассмотрим ориентированный граф, заданный следующим входным файлом. Построим графическое представление графа, определяемого этим файлом.

1 2 1

1 5 3

2 3 3

2 4 3

2 5 8

3 4 1

3 5 -5

4 3 2

5 4 4

Матрица весов дуг данного графа имеет вид

.

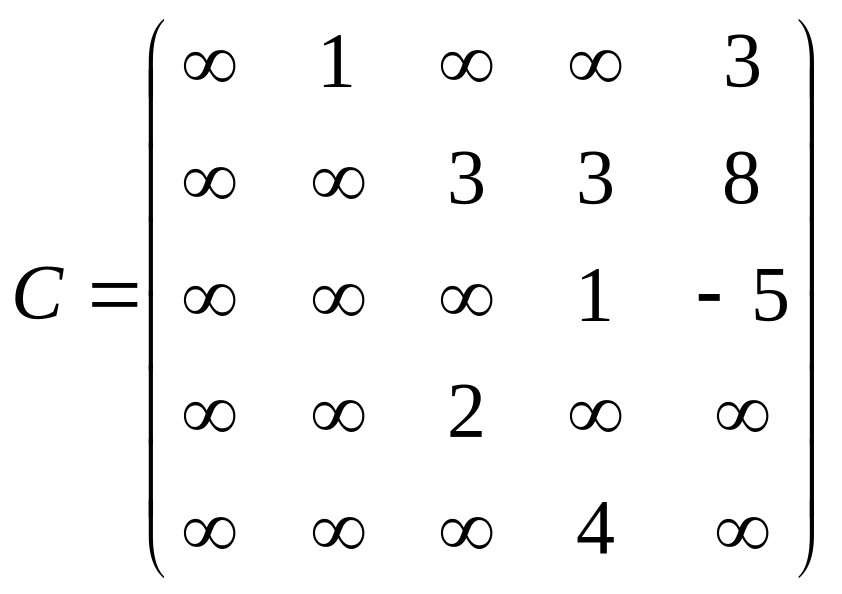Пусть . Вычислим минимальные расстояния от вершины s до всех вершин графа. Выполним один шаг алгоритма Форда-Беллмана подробно, затем результаты работы алгоритма представим в виде таблицы.

Номер шага k	D
	1	2	3	4	5
	0	1			3
1	0	1	4	4	-1
2	0	1	4	3	-1
3	0	1	4	3	-1

Восстановим кратчайший путь от s до вершины .

, , так как

, , так как

, , так как

, , так как

. В результате СТЕК имеет вид

1

2

3

5

4

Следовательно, кратчайший путь между вершинами 1 и 4, длина которого равна 3: 1  2  3  5  4.

2. Рассмотрим неориентированный граф, заданный следующим входным файлом. Построим графическое представление графа, определяемого этим файлом.

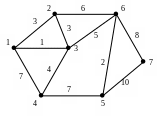
1 2 3

1 3 1

1 4 7

2 3 3

2 6 6

3 4 4

3 6 5

4 5 7

5 6 2

5 7 10

6 7 8

Перед построением остова , разбиение содержит 7 компонент, каждая компонента связности содержит одну вершину, т.е. .

Упорядочим рёбра в порядке возрастания весов. Результат работы алгоритма Краскала оформим в виде таблицы. Обозначим через:

– ребро графа;

– вес ребра ;

– вес остова.

Если ребро графа добавляется в остов (его инцидентные вершины принадлежат разным связным компонентам остова), то и изменятся, а, следовательно, в таблицу записываем изменённые разбиение и вес остова. В противном случае соответствующие ячейки таблицы остаются пустыми.

(1, 3)	1		1
(5, 6)	2		3
(1, 2)	3		6
(2, 3)	3
(3, 4)	4		10
(3, 6)	5		15
(2, 6)	6
(1, 4)	7
(4, 5)	7
(6, 7)	8		23
(5, 7)	10

Таким образом кратчайший остов графа суммарного веса имеет вид