МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГБОУ ВО

“Воронежский государственный УНИВЕРСИТЕТ

ИНЖЕНЕРНЫХ технологиЙ”

Ю.В. БУГАЕВ, И.Ю. ШУРУПОВА,

О.В. АВСЕЕВА, Л.А. КОРОБОВА

ТЕОретИЧЕСКИЕ ОСНОВЫ

ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

Для студентов, обучающихся по направлению

09.03.02 – “Информационные системы и технологии”,

очной формы обучения

ВОРОНЕЖ

2016

УДК 681.3.06; 51(075)

ББК

Т-

Научный редактор доцент Л.А. КОРОБОВА

Рекомендуется к размещению

в ЭОС и ЭБ ВГУИТ

Бугаев, Ю.В.

Т- Теоретические основы информационных технологий. Лабораторный практикум [Электронный ресурс]: учеб. пособие / Ю. В. Бугаев, И. Ю. Шурупова, О. В. Авсеева, Л. А. Коробова; Воронеж. гос. ун-т инж. технол. – Воронеж : ВГУИТ, 2016. – 80 с. – [ЭИ]

ISBN

Учебное пособие разработано в соответствии с требованиями ФГОС ВО подготовки бакалавров направления 09.03.02 – “Информационные системы и технологии”. В пособии изложена методика выполнения лабораторных работ базовой части блока Б1, приведены варианты заданий.

УДК 519.6; 683.1

Без объявл. ББК

ОК2(03) - 2007

ISBN © Бугаев Ю. В., Шурупова И. Ю.,

Авсеева О. В., Коробова Л. А. 2016

© ФГБОУ ВО “Воронеж. гос. ун-т инж. технол.”, 2016

Оригинал-макет данного издания является собственностью Воронежской государственной технологической академии, его репродуцирование (воспроизведение) любым способом без согласия академии запрещается.

Предисловие

Процесс изучения дисциплины направлен на формирование компетенции:

• способностью использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования (ОПК-2).

В результате освоения дисциплины студент должен:

знать

• основные понятия и методы теоретической информатики;

• способы представления дискретных структур в информационных системах;

уметь

• применять математический аппарат для построения моделей описания и решения прикладных задач;

владеть

• навыками моделирования прикладных задач методами теоретической информатики;

• навыками построения алгоритмов решения прикладных задач.

Лабораторная работа №1 операции над множествами

Цель работы: изучение операций над множествами и их свойств, методов доказательства утверждений теории множеств.

Теоретические сведения

Множеством называется совокупность некоторых объектов, объединенных общим признаком.

Для множеств вводятся следующие отношения.

Множество А нестрого включено в множество В (обозначается АВ) если для любого элемента хА, следует что хB. Нестрогое включение не исключает совпадения множеств.

Множество А строго включено в множество В (обозначается АВ) если:

1. АВ;

2. существует yB, такой, что yA.

Множество А совпадает с множеством В (А = В), если все элементы множества В являются элементами множества В и все элементы множества В являются элементами множества А, т.е.

(АВ и ВА)  (А = В).

Большинство утверждений теории множеств связано с равенством двух множеств и включением одного множества в другое. Поэтому детально разберёмся в методах доказательства этих фактов.

1. Доказательство нестрогого включения АВ. Для этого нужно доказать, что любой элемент x, принадлежащий множеству А одновременно является элементом множества В, т.е.

( x  А)   (x  В).

2. Доказательство строгого включения АВ состоит из двух частей:

1. АВ;

2.  y: y  B и y  A.

3. Доказательство равенства А = В сводится к доказательству двух включений А  В и В  А.

Дадим определения операций над множествами, используя способ задания множества характеристическим свойством или формулой теории множеств.

1. Дополнение : .

2. Пересечение : .

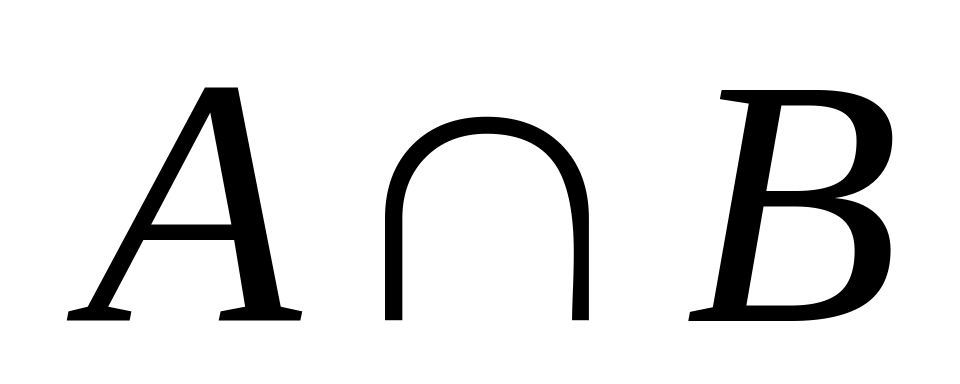3. Объединение : .

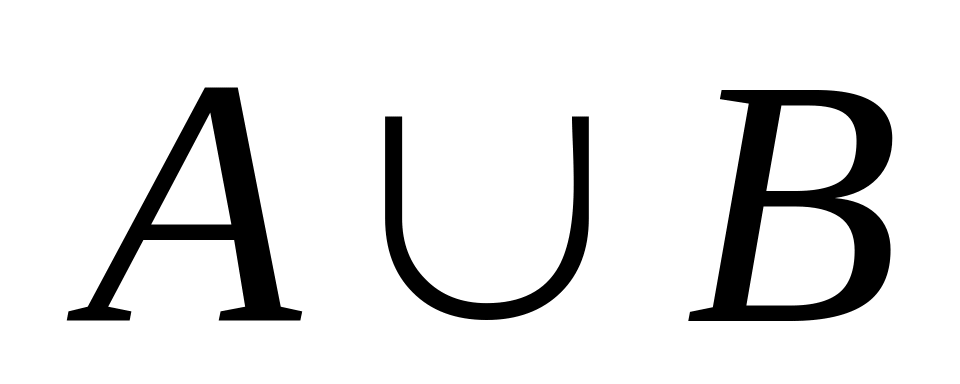4. Разность : .

5. Симметрическая разность : .

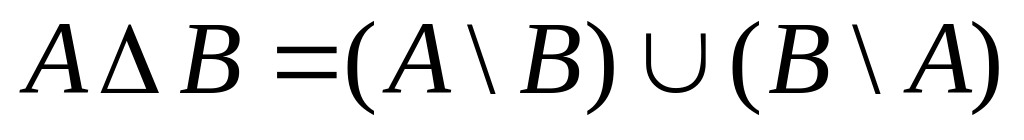В доказательствах будем также использовать следующие краткие обозначения, для того чтобы расписать принадлежность элемента множеству, построенному с помощью операций над множествами.

 

Фигурная скобка и запятая здесь, как и прежде, обозначает выполнение обоих свойств.



Квадратная скобка означает выполнение хотя бы одного из свойств. Таким образом, доказательство в дальнейшем распадается на два случая, для которых рассуждения проводятся отдельно, каждое в своей строке.





Распишем также, что означает, что элемент не принадлежит множеству, построенному с помощью операций над множествами.

 

 

Если из условия следует свойство о принадлежности элемента одному множества (например ) и ничего не известно относительно другого (B), которое участвует в формуле доказываемого утверждения, то необходимо рассмотреть оба случая и в обоих случаях вывести (или опровергнуть) требуемое свойство.

Утверждение вида эквивалентно включениям или .