МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Ульяновский государственный педагогический университет» изучение распределения термоэлектронов по скоростям

Методические указания

по проведению лабораторной работы

по дисциплине «Молекулярная физика»

Составитель: Э. Н. Старов

Ульяновск

2012

УДК 530.1 (076)

ББК 22.317

С 77

Рецензент доцент кафедры «Общенаучные дисциплины» самолетостроительного факультета Ульяновского государственного технического университета доцент, канд. техн. наук В. И. Кочергин

Одобрено секцией методических пособий научно-методического совета университета

И

С

зучение распределения термоэлектронов по скоростям : методические указания к лабораторной работе по дисциплине «Физика» / сост. Э. Н. Старов.  Ульяновск : УлГТУ, 2012.  17 с.

Составлены в соответствии с программой курса «Физика».

Предназначены для студентов всех форм обучения специальности 16010065 «Самолето- и вертолетостроение», 16010062 «Авиастроение», 23040062 «Информационные системы и технологии» и обеспечивают возможность подготовки к выполнению работ, проверки результатов подготовки перед выполнением работы, дают возможность систематизировать и проанализировать результаты ее выполнения.

Подготовлены на кафедре «Общенаучные дисциплины».

УДК 530.1 (076)

ББК 22.317

© Старов э. Н., составление, 2012

© Оформление. УлГТУ, 2012

СОДЕРЖАНИЕ

ВВЕДЕНИЕ…………………………………………………………………... 4

Проведение измерений и обработка результатов……………….………….11

ВОПРОСЫ ПРИ ДОПУСКЕ К РАБОТЕ…………………………………...16

КОНТРОЛЬНЫЕ ВОПРОСЫ ПРИ СДАЧЕ……………………………… 16

БИБЛИОГРАФИЧЕСКИЙ СПИСОК………………………………….……17

ЛАБОРАТОРНАЯ РАБОТА

ИЗУЧЕНИЕ РАСПРЕДЕЛЕНИЯ ТЕРМОЭЛЕКТРОНОВ

ПО СКОРОСТЯМ

Цель работы:

1. Ознакомиться с теорией Максвелла распределения молекул по скоростям.

2. Экспериментально изучить распределение электронов по скоростям в электронном облаке, вблизи катода электронной лампы.

ВВЕДЕНИЕ

Молекулярно-кинетическая теория рассматривает физические тела, состоящими из множества атомов или молекул, у которых непрерывно и хаотично изменяются скорости, импульсы и энергии.

Такие сложные системы из огромного числа частиц изучаются статистическими методами. Одним из основных понятий такого метода является понятие функции плотности вероятности f(x). Если имеется совокупность из N частиц, для которой случайным образом изменяется некая величина х, то f(x) определяет вероятность dP(x) того, что dN частиц из этой совокупности будут иметь величину х в пределах от х до х+dx

(1)

Согласно смыслу выражения (1), функция плотности f(x) удовлетворяет двум условиям:

f(x)≥0 и (2)

Рассмотрим идеальный газ, находящийся в замкнутом объеме, температура которого поддерживается постоянной. В результате большого числа столкновений установится равновесное состояние, при котором число молекул в заданном интервале скоростей уже не изменяется со временем. Обозначим концентрацию молекул через n, тогда согласно равенству (1), число молекул dn в единице объема, скорости которых заключены в интервале V, V+dV будет равно

(3)

Распределение молекул газа по модулю скорости описывается функцией плотности вероятности, впервые полученной Максвеллом:

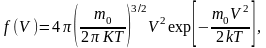(4)

где m₀ - масса одной молекулы, k - постоянная Больцмана, T - температура по шкале Кельвина.

Смысл функции ясен из (3):

(5)

т. е. значение функции численно равно плотности вероятности того, что скорость молекулы попадает в единичный интервал скоростей вблизи заданной скорости V.

Вероятность того, что скорость молекулы расположена в интервале скоростей от V₁ до V₂:

(6)

Вид функции показан на рисунке 1.

_f(V)

Т=const

V_н V_ср

С V

Рис. 1. Распределение Максвелла по скоростям

Из формулы (4) видно, что f(V) обращается в нуль при V=0 и V→ ∞. Из условия максимума можно найти значение V_H (наивероятнейшая скорость) при котором функция принимает наибольшее значение:

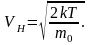(7)

Среднее значение скорости молекул с использованием функции плотности находится из равенства:

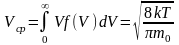(8)

Аналогично находится среднее значение квадрата скорости:

Под среднеквадратичной скоростью понимают величину:

(9)

_{С изменением температуры график функции изменяется так, что площадь под кривой} f(V) остается постоянной (так как т. е. вероятность того, что скорость молекулы находится в интервале от 0 до ∞ равна единице). Максимум функции понижается и смещается вправо, так как V_н ~

f(V)

Т₁

Т₂>Т₁

V_н1 V_н2 V

Рис. 2. Распределение Максвелла для двух различных температур

Как видно из рис. 2 доля молекул 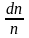со скоростями в интервале V, V+dV при V>V_н возрастает, а при V<V_н уменьшается.

В ряде случаев удобно ввести безразмерный параметр - относительную скорость , тогда с учетом (7) формула (4) запишется в виде:

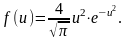(10)

Удобство этой функции распределения в том, что она не зависит от температуры и массы молекул газа. График f(u) приведен на рис. 3.

f(u)

1,0 0,83

0,8

0,6

0,4

0,2

0 0,4 0,8 1,2 1,6 2,0 2,4 u

Рис. 3. Распределение Максвелла для относительной скорости