1.2. Типический (стратифицированный, расслоённый, районированный) отбор

Типический отбор используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько типических групп. При обследовании населения такими группами могут быть, например, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасль или подотрасль, форма собственности и т.п. Типический отбор предполагает выборку единиц из каждой типической группы собственно-случайным или механическим способом.

Наиболее часто применяется пропорциональное размещение (пропорциональная типическая выборка), когда количество отбираемых в выборку единиц пропорционально удельному весу данной группы по числу единиц в генеральной совокупности, то есть число наблюдений по каждой группе определяется по формуле ,

где – число наблюдений из -й типической группы;

− общий объём выборки;

− объём -й типической группы в генеральной совокупности;

− объём генеральной совокупности.

При отборе пропорционально численности группы

. В этом случае средняя ошибка средней:

− при повторном отборе

− при бесповторном отборе

Например. Для определения средней заработной платы рабочих завода была произведена 20%-я бесповторная выборка по цехам с отбором единиц пропорционально численности групп (таблица 1.2.1).

Таблица 1.2.1 − Результаты обследования рабочих завода

Цех	Объём выборки, чел., ni	Средняя заработная плата, руб.,	Среднее квадратическое отклонение, руб.,
1	120	26 873	30
2	100	27 886	80
3	180	28 900	60
Итого	400	-	-

С вероятностью 0,997 (t=3) определить пределы, в которых находится заработная плата всех рабочих завода.

Решение:

1. Находим общую выборочную среднюю заработную плату:

руб.

2. Рассчитаем среднюю из групповых дисперсий:

.

3. Определяем среднюю ошибку выборочной средней заработной платы руб.

4. Находим предельную ошибку выборочной средней заработной платы

руб.

5. Определяем пределы изменения генеральной средней

Средняя ошибка доли при пропорциональном типическом отборе:

где ;

− при бесповторном отборе:

Второй вариант выбора единиц в типическую группу пропорционально внутригрупповой дифференциации признака, то есть оптимальное размещение (непропорциональная типическая выборка). Расчёт объёма выборки из каждой типической группы производится по формуле ,

где − среднее квадратическое отклонение признака в i-й группе генеральной совокупности.

Средняя ошибка средней непропорциональной типической выборки:

− при повторном отборе ,

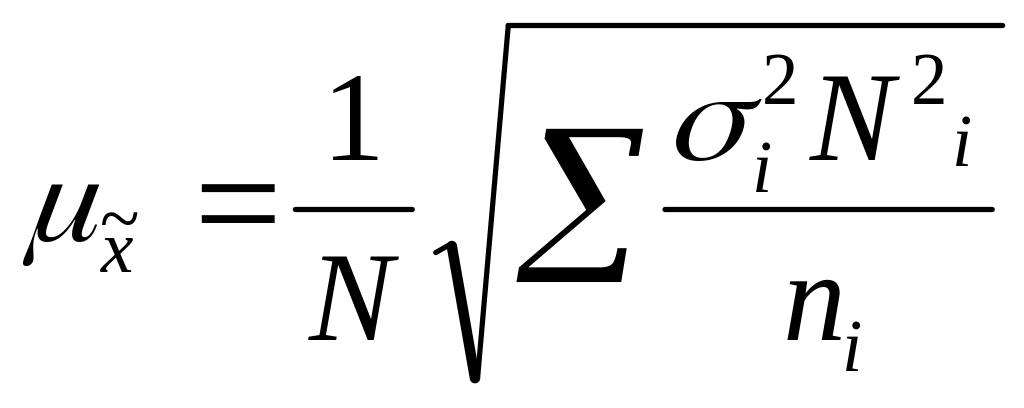− при бесповторном отборе .

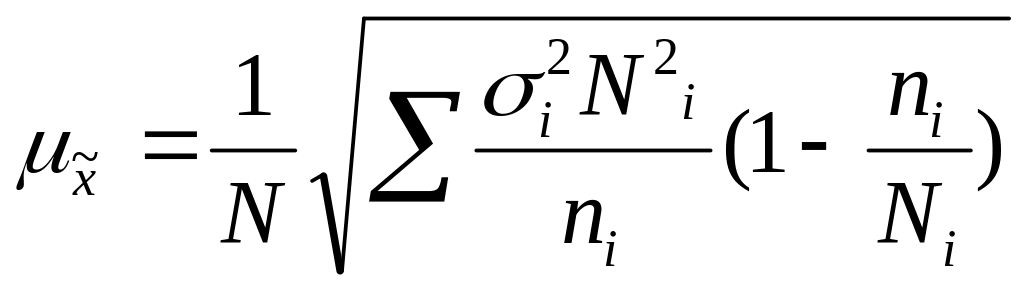Например. 10% бесповторный типический отбор рабочих предприятия, пропорциональный дифференциации признака (число дней временной нетрудоспособности), привёл к следующим результатам (таблица 1.2.2).

Таблица 1.2.2 − Результаты обследования рабочих предприятия

Цех	Всего рабочих, чел, Ni	Дисперсия числа дней временной нетрудоспособности,
1	1 000	49
2	1 400	25
3	800	16
Итого	3 200	-

С вероятностью 0,954 определить предельную ошибку выборки.

Решение:

1. Определим необходимый объём выборки по каждому цеху:

; ;

2. Рассчитаем среднюю ошибку выборки =

=

3. Находим предельную ошибку выборки с вероятностью 0,954 (t=2)

Разновидностью типической является районированная выборка, при которой отбор единиц для наблюдения проводится из групп, представленных административно-территориальными образованиями.

Задачи

2.1. На металлургических заводах корпорации работают 100 формовщиков и 200 литейщиков. Проведено районированное изучение среднемесячной заработной платы 60 рабочих с пропорциональным распределением их по специальностям в соответствии с удельным весом в общем количестве рабочих. Внутри каждой группы применялся метод повторного отбора. В результате получены следующие данные:

Показатель	Формовщики	Литейщики
Месячная заработная плата, руб. Среднее квадратическое отклонение по заработной плате, руб.	38 000 540	41 100 880

Определите предел ошибки репрезентативности при установлении средней заработной платы, гарантировав результат с вероятностью 0,954.

2.2. Для определения урожайности зерновых культур проведена типическая пропорциональная выборка 100 хозяйств региона различных форм собственности:

Хозяйства (по формам собственности)	Количество обследованных хозяйств	Средняя урожайность	Дисперсия урожайности в каждой группе
Коллективная Акционерные общества Крестьянские (фермерские)	30 50 20	18 20 28	15 25 40
Итого	100	-	-

Необходимо с вероятностью 0,954 определить предельную ошибку выборочной средней и доверительные пределы средней урожайности зерновых культур по всем хозяйствам региона.

2.3. По результатам 5%-го выборочного обследования, проведённого методом пропорционального типического отбора, с целью изучения уровня оплаты труда по отрасли получены следующие данные:

Тип предприятия	Средняя заработная плата, руб.	Число обследованных работников	Среднее квадратическое отклонение, руб.
Среднее	32 500	800	1 100
Малое	28 900	200	800

Определите с вероятностью 0,9996 пределы, в которых находится средняя заработная плата работников отрасли.

2.4. В области 150 тыс. молочных коров. Из них в районе А – 70 тыс. коров, в районе Б – 50 тыс. коров, в районе В – 30 тыс. коров. Для определения средней удойности коров области произведена 1%-я типическая выборка с отбором единиц пропорционально численности коров в районах (внутри районов применялся случайный бесповторный метод отбора). Результаты выборки представлены в таблице:

Районы	Средний удой коров, кг	Среднее квадратическое отклонение
А Б В	3 200 3 000 2 500	700 400 240

С вероятностью 0,997 определите пределы, в которых находится удойность коров.

2.5. Для установления дальности пробега машин на трёх автобазах методом случайного бесповторного отбора было отобрано 300 путёвок. Из них на автобазе № 1 – 150, № 2 – 60, № 3 – 90 путёвок. В результате обследования установлено, что доля машин с дальностью пробега свыше 100 км составляет на автобазе № 1 –30 %, на автобазе № 2 – 15 % и на автобазе № 3 – 25 %. С вероятностью 0,954 определите предел, в котором находится доля машин с дальностью пробега, превышающей 100 км, по трём автобазам при условии, что выборка составляет 5 %.

2.6. С целью определения доли расходов на питание населением города А методом типической выборки был произведён 5%-й отбор семей. Внутри типов производилась случайная бесповторная выборка. Результаты выборки представлены в таблице:

Тип семей	Число лиц	Доля расходов на питание (в %)
Одинокие Семейные	30 70	33 45

С вероятностью 0,954 определите предел, в котором находится доля расходов на питание семей города А.

2.7. Для определения женского труда в одной из отраслей обрабатывающей промышленности все предприятия отрасли были разбиты на три группы − крупные, средние и мелкие. По численности рабочих эти группы распределились следующим образом: крупные − 50%, средние − 40%, мелкие − 10%. От общего числа рабочих всей отрасли. В порядке бесповторной типической выборки был произведён отбор 10 000 человек с пропорциональным распределением по группам, в результате которого доля мужчин оказалась равной в крупных предприятиях 60%, в средних − 50%, в мелких − 45%. Определите с вероятностью 0,997, в каких пределах заключена доля женщин среди всех рабочих данной отрасли.

2.8. Для изучения влияния общего стажа работы на квалификацию рабочих механического цеха была проведена бесповторная типическая выборка с непропорциональным распределением (по 50 рабочих в каждой группе), которая дала следующие результаты:

Группа рабочих по стажу работы	Общее число рабочих в группе (человек)	Объём выборки	В том числе по разрядам
			1	2	3	4	5	6
До 10 лет Свыше 10 лет	600 400	50 50	10 -	23 5	14 8	2 17	1 14	- 6

По этим данным определите: 1) необходимый объём выборки по каждой из групп рабочих при определении среднего разряда рабочих цеха, который даст наиболее точные результаты; 2) возможные пределы среднего разряда рабочих цеха с вероятностью 0,954; 3) необходимую численность выборки по каждой из групп рабочих при определении доли рабочих высокой квалификации (5-й и 6-й разряды), которая даст наиболее точные результаты; 4) возможные пределы доли рабочих в цехе, имеющих высокую квалификацию (5-й и 6-й разряды), с вероятностью 0,683.

2.9. Для изучения сортности продукции акционерного общества была проведена бесповторная типическая выборка с непропорциональным отбором, которая дала следующие результаты:

№ цеха	Объём продукции, шт.	Объём выборки, шт.	Сортность продукции, шт.
			высший	первый
1 2	500 800	50 100	20 20	30 80

По этим данным определите: 1) необходимую численность выборки по каждому из цехов при определении доли продукции высшего сорта, которая даст наиболее точные результаты; 2) возможные пределы доли продукции высшего сорта с вероятностью 0,954.

2.10. В целях изучения производительности четырёх типов станков, производящих одни те же операции, была произведена 10%-я типическая выборка с непропорциональным отбором единиц:

Тип станков	Всего станков	Среднее число деталей, изготовленных на станке за час работы, штук	Среднее квадратическое отклонение
I II III IV	150 300 450 100	400 520 700 610	40 20 50 70

Определите: 1) необходимую численность выборки по каждому типу станков при определении производительности, которая даст наиболее точные результаты; 2) с вероятностью 0,997 определите предел, в котором находится среднее число деталей, производимых на всех станках.

2.11. С целью определения среднего стажа работы рабочих завода (в годах) произведена 10%-я бесповторная выборка способом типического пропорционального отбора. Результаты обследования сведены в следующую таблицу:

Группа рабочих по полу	Группа рабочих по стажу работы						Итого
	до 2	2 − 5	5 − 10	10 − 20	20 − 25	25 и выше
Мужчины Женщины	20 20	80 50	100 80	60 43	30 5	10 2	300 200
Всего	40	130	180	103	35	12	500

Определите: 1) с вероятностью 0,954 для всех рабочих предприятия предельную ошибку среднего стажа работы всех рабочих; 2) пределы, в которых находится средний стаж их работы; 3) предельную ошибку доли рабочих со стажем до 5 лет с вероятностью 0,997; 4) пределы, в которых находится число рабочих со стажем до 5 лет; 5) необходимую численность непропорциональной выборки по полу рабочих, которая наиболее точные результаты; 6) с вероятностью 0,954 определите предел, в котором находится средний стаж всех рабочих; 7) необходимую численность выборки по полу при определении доли рабочих со стажем до 5 лет, которая даст наиболее точные результаты; 8) предел, в котором находится доля рабочих со стажем до 5 лет с вероятностью 0,997. Сравните полученные результаты и сделайте выводы.

2.12. По данным выборочного обследования (20%-й типический отбор) трудовое участие женщин в общественном производстве характеризуется следующими данными:

Наличие детей в возрасте до 12 лет	Число женщин	В среднем отработано на одну женщину, чел.-дней	Среднее квадратическое отклонение отработанных чел.-дней
Без детей Один ребенок Двое и больше детей	200 120 80	158 150 130	10 20 15

С вероятностью 0,954 определите ошибку выборки для среднего числа отработанных человеко-дней на одну женщину. С какой вероятностью можно утверждать, что среднее число отработанных за год человеко-дней на одну женщину не меньше 147,4?