2.4 Сглаживание исходной информации

Сглаживание исходной информации – это замена таблицы опытных точек другой таблицей близких к ним точек, лежащих на достаточно гладкой кривой.

Рис. 2.5. Линейная и квадратичная аппроксимации

Сглаживание применяют:

- для устранения ошибок замеров, что необходимо для численного дифференцирования или интегрирования экспериментальных данных;

- если количество экспериментальных точек велико, то подбор эмпирической формулы может оказаться весьма затруднительным.

Сглаживание производится с помощью многочленов (рис. 2.6). Наилучшее сглаживание получается для средних точек, когда учитывается информация о поведении функции по обе стороны сглаживаемой точки. Количество точек для сглаживания выбирают нечетным.

Линейным сглаживанием называется сглаживание многочленом первой степени.

Рис. 2.6. Сглаживание экспериментальных точек

Формулы линейного сглаживания по трем точкам:

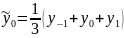
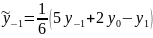
В этих формулах приняты следующие обозначения. Средней точке приписывается индекс «0», симметричные точки получают при этом индекс ±1. Сглаженные значения обозначаются волнистой чертой сверху. Основной формулой служит формула сглаживания средней точки, т.е. формула для . Остальные формулы используются для экспериментальных данных, расположенных на внешнем контуре таблицы.

Пример

Исходные данные		Сгл.данные
X	y	y
0	431	424
1	409	423
2	429	420
3	422	460
4	530	486

Рис. 2.7. Виды сглаживания

2.5 Вопросы для самопроверки

1. Что такое аппроксимация?

2. Что такое уравнение регрессии?

3. Для чего применяется аппроксимация экспериментальных данных?

4. В чем заключается метод средних?

5. Каковы основные шаги при аппроксимации методом наименьших квадратов?

6. Что общего и в чем различие между методами независимых функций и наименьших квадратов?

7. Какие функции называются линейно независимыми?

8. Как влияет количество экспериментальных точек на точность аппроксимации?

9. Как оценить точность используемого метода аппроксимации?

10. Перечислите достоинства и недостатки методов средних, наименьших квадратов и независимых функций

11. Что такое сглаживание? Для чего оно применяется?

12. Какие виды аппроксимаций можно находить методами средних, наименьших квадратов и независимых функций?

13. Что такое полиномы Чебышева? В чем заключается их ортогональность?

14. Как определить вид аппроксимируемой зависимости?

15. Какое минимальное число экспериментальных точек можно аппроксимировать методом наименьших квадратов?

16. Какое максимальное число экспериментальных точек можно аппроксимировать методом средних?

17. Какой метод аппроксимации следует использовать для аппроксимации зависимости вида у=αe^-x?