2.3 Аппроксимация в виде системы линейно независимых функций

Применяется, когда вид функции заранее не известен. Пусть

где - ортогональные многочлены Чебышева на множестве точек х₁,х₂,…х_n.

Условие ортогональности

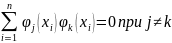
Согласно МНК

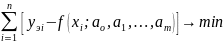
откуда

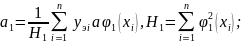
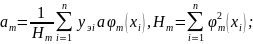
Оценка любого параметра α_i зависит только от соответствующей базисной функции φ(х_i). Сами базисные функции удобно выбирать в виде многочленов:

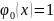
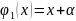
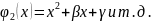
Коэффициенты α,β,γ выбирают из условия ортогональности

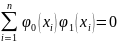
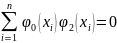
Полученные отношения проиллюстрируем примером.

Известна экспериментальная зависимость предела прочности от размера d[мм] зерна рекристализированного металла (см. табл.2.1).

Произведем линейное преобразование переменных:

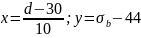
Примем линейную модель вида 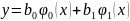с базисными функциями

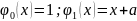
Из условия ортогональности найдем α:

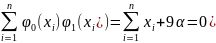
В силу симметрии 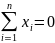, поэтому

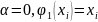
По методу наименьших квадратов находим параметры b₀, b₁:

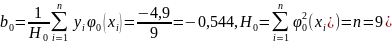
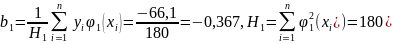
Таким образом получена линейная зависимость вида у=-0,544-0,367x.

Примем квадратичную модель вида 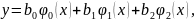где

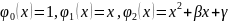
Из условия ортогональности получим:

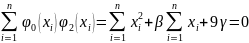
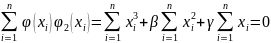
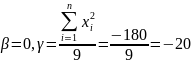
Следовательно,

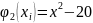
Найдем b₂: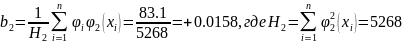

Тогда квадратичная зависимость примет вид

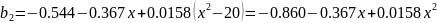
Порядок и результаты проведенных расчетов представлены в табл. 2.1 и на рис. 2.5.

Таблица 2.1 Расчет аппроксимации при помощи линейно независимых функций

n	d	σ b	Xi=ϕ1	yi=yϕ0	yix=yiϕ1	ϕ2	Yϕ2	Линейная модель		Квадратичная модель
								Yрасч	y-yрасч	Yрасч	y-yрасч
1	50	47,1	-8	3,1	-24,7	44	135,8	2,392	0,695	3,087	0,018
2	90	44,8	-4	0,9	-3,4	-4	-3,4	0,924	-0,063	0,861	-0,063
3	100	44,4	-3	0,4	-1,1	-11	-4,2	0,557	-0,174	0,383	0,018
4	120	43,6	-1	-0,5	0,5	-19	9,1	-0,177	-0,300	-0,477	0,077
5	130	43,2	0	-0,9	0,0	-20	17,2	-0,544	-0,316	-0,860	0,06
6	140	42,6	1	-1,2	-1,2	-19	23,0	-0,911	-0,300	-1,211	-0,189
7	160	42,3	3	-1,8	-5,5	-11	20,0	-1,645	-0,174	-1,819	0,118
8	170	41,9	4	-2,1	-8,3	-4	8,3	-2,012	-0,063	-2,075	-0,022
9	210	41,2	8	-2,8	-22,3	44	-122,5	-3,48	0,695	-2,785	-0,022
∑			180	-4,9	-66,1	5268	83,2	-4,896	1,315	-4,896	0,0648
			H1			H2		∑( y-yрасч)2		∑( y-yрасч)2

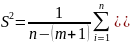
Тогда для линейной модели