1.3. Погрешности косвенных измерений

Во многих случаях искомая величина является функцией нескольких измеряемых прямым способом величин.

Пусть искомая величина z определяется из прямых измерений а, т.е.

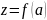
Обозначим точное значение результата косвенных измерений через

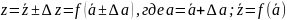
Полагая величину абсолютной погрешности прямых измерений ∆α очень малой по сравнению с ᾱ, можно для определения погрешности косвенных измерений воспользоваться связью дифференциала функции df с бесконечно малым приращением аргумента:

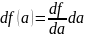
Тогда

=

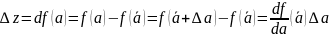Относительная погрешность равна

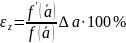
Рассмотрим теперь случай, когда искомая величина z является функцией двух переменных a и b, определяемых из прямых измерений, т.е.

Пусть

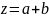
Величина а определяется из серии к измерений а_i, i=1,2,... ,k, a величина b - из серии m измерений b_j, j=1,2, …,m.

Истинные значения a и b связаны со средними значениями и соотношениями

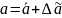
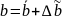
где случайные возможные значения

Абсолютная погрешность результата косвенных измерений

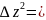
Черта сверху означает усреднение по распределению соответствующих случайных величин. Член равен нулю в силу симметрии кривых распределения и

В самом общем случае

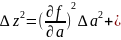
Следовательно,

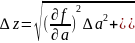
где и 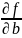- частные производные функции f(a,b) по переменным a и b соответственно.

Аналогично для z=f(a,b,c,..) получаем

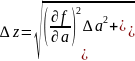
Используя последнюю формулу, найдем погрешность измерения произведения двух величин z=ab

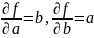
Тогда абсолютная погрешность

Относительная погрешность

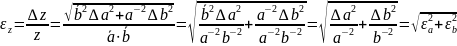
Обработку результатов косвенных измерений следует проводить в следующем порядке:

1. Для каждой серии измеренных величин, входящих в определение искомой величины, проводится обработка как для случая прямых измерений. При этом для всех измеряемых величин задают один и тот же уровень значимости α.

2. Находят границы доверительного интервала для результата косвенных измерений ∆f.

3. Окончательный результат записывают в виде

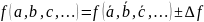
Определяют относительную погрешность результата серии косвенных измерений:

Все вычисления следует проводить с числом значащих цифр, превышающих на единицу число значащих цифр, полученных при косвенных измерениях. Если ошибка измерения со составляет 1-10%, то необходимо указать не более трех значащих цифр. 0,1-1%- не более четырех значащих цифр.

1.4. Выявление и исключение промахов

Если серия из небольшого числа измерений содержит грубую погрешность - промах, то наличие этого промаха может сильно исказить как среднее значение измеряемой величины, так и границы доверительного интервала. Обычно промах имеет резко отличающееся от других измерений значение и его исключают из серии измерений. Для обнаружения промаха необходимо рассмотреть переменную Ɵ:

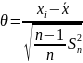(1.6)

которая в случае или называется критерием максимальных относительных отклонений или критерием совместности.

В формуле (1.6) - среднее значение

а 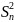дисперсия

Дисперсия - это мера изменчивости, рассеивания любого опыта от среднего арифметического

Наличие отклонений свидетельствует об изменчивости значений повторных опытов. Чем больше дисперсия, тем больше рассеяны значения параллельных опытов около среднего значения.

Если Ɵ_расч>Ɵ_табл, то подозреваемое значение х_i следует считать промахом.

Пример: в таблице приведены результаты параллельных опытов, n=6

i	1	2	3	4	5	5
xi	53,4	54,6	154,7	155,0	164,3	154,5

Значения x₅=164,3 является подозреваемым на промах:

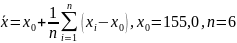
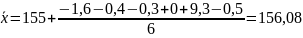
Затем вычисляем расчетное значение Ɵ

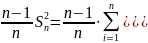
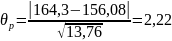
Таблица 1.4 - Фрагмент таблицы Ɵ-критерия при α=0.05

n	3	4	5	6	8	10	12	15	20	30
θ	1,41	1,69	1,87	2,00	2,17	2,29	2,39	2,49	2,62	2,79

Поэтому значение x₅=164,3 считается промахом. Его исключают из серии опытов.