
- •Методология научного эксперимента
- •Введение
- •1 Общие сведения об эксперименте
- •1.1 Что такое эксперимент?
- •1.2 Элементы теории измерений.
- •1.3. Погрешности косвенных измерений
- •1.4. Выявление и исключение промахов
- •1.5. Графическая обработка результатов эксперимента
- •1.6 Вопросы для самопроверки
- •1.7 Задачи к разделу
- •2 Аппроксимация экспериментальных данных
- •2.1 Метод средних
- •2.2 Метод наименьших квадратов
- •2.3 Аппроксимация в виде системы линейно независимых функций
- •2.4 Сглаживание исходной информации
- •2.5 Вопросы для самопроверки
- •Задачи и упражнения к разделу
- •3. Построение плана многофакторного эксперимента
- •3.1. Планирование факторного эксперимента
- •3.2. Полный факторный эксперимент
- •3.3. Дробный факторный эксперимент
- •3.4. Математическая обработка факторного эксперимента
- •3.5. Планы второго порядка
- •3.5.1. Ротабельное планирование
- •3.5.2. Некомпозиционный план
- •3.6. Вопросы для самопроверки
- •3.7. Задачи и упражнения к разделу
- •4. Поиск оптимальных условий в экспериментальных исследованиях
- •Одномерные методы поиска экстремума
- •Метод дихотомии
- •4.1.2. Метод Фибоначчи
- •4.1.3. Метод «золотого сечения»
- •Многомерные методы поиска
- •4.2.1 Метод Гаусса-Зайделя
- •Метод крутого восхождения
- •Симплекс-метод
- •4.3. Вопросы для самопроверки
- •4.4. Задачи и упражнения к разделу
- •5. Дисперсионный анализ
- •5.1. Основные понятия дисперсионного анализа
- •5.1.1 Однофакторный дисперсионный анализ
- •Двухфакторный дисперсионный анализ
- •5.2. Латинские и греко-латинские квадраты
- •5.3. Вопросы для самопроверки
- •5.4. Задачи и упражнения к разделу
5. Дисперсионный анализ
5.1. Основные понятия дисперсионного анализа
В любом эксперименте средние значения измеряемых величин меняются в связи с изменениями качественных, количественных и случайных факторов. Исследование влияния тех или иных факторов на изменчивость средних значений Y является задачей дисперсионного анализа. Дисперсионный анализ устанавливает, какие из факторов оказывают наибольшее влияние на Y, какие из них могут быть исключены из модели из-за их незначимости. Степень влияния фактора хi, называется эффектом этого фактора и изображается большой латинской буквой. Тогда дисперсионная модель процесса может быть представлена уравнением
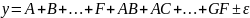
где A - эффект влияния на Y фактора х1, B - фактора х2, АВ-взаимодействия x1 x2 и т.д.; ε-ε -ошибка эксперимента.
Чтобы оценить слияние отдельного фактора на Y, необходимо
Произвести разложение суммарной дисперсии на составляющие, обусловленные независимыми факторами:

2. Оценить
значимость соответствующей дисперсии
в сравнении с дисперсией ошибки по
критерию Фишера. Если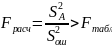 ,
то фактор А значимый.
,
то фактор А значимый.
5.1.1 Однофакторный дисперсионный анализ
В таблице приведены наблюдаемые значения целевой функции уij при изменении фактора х1 на a уровнях (i=1,2..., a). На каждом уровне проведено по n повторных опытов (j=1,2..., n). Эксперимент состоит из αn опытов.
Номер уровня фактора |
Результаты испытаний |
Среднее значение |
дисперсия |
I=1 |
y11,y12,…,y1j,…,y1n |
|
S12 |
I=2 |
Y21,y22,…,y2j,…,y2n |
2 |
S22 |
… |
… |
… |
|
I=a |
Ya1,ya2,…,yaj,…,yan |
a |
Sa2 |
Дисперсионное уравнение имеет вид y=A±ε.
Общая
дисперсия:
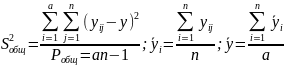
Дисперсия
на каждом уровне:
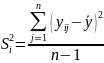 .
.
Дисперсия
фактора x1:
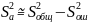
Проверка
значимости:

Двухфакторный дисперсионный анализ
X1 |
X2 |
Суммы |
||||
j=1 |
j=2 |
… |
j=b |
|||
i=1 |
y111 |
y121 |
…. |
y1b1 |
y1•1 |
|
y112 |
y122 |
… |
y1b2 |
y1•2 |
||
… |
… |
… |
… |
… |
||
y11n |
y12n |
… |
y1bn |
y1•n |
||
суммы |
y11• |
y12• |
… |
y1b• |
y1•• |
|
i=2 |
y211 |
y221 |
… |
y2b1 |
y2•1 |
|
y212 |
y222 |
… |
y2b2 |
y2•2 |
||
… |
… |
… |
… |
… |
||
y21n |
y22n |
… |
y2bn |
y2•n |
||
суммы |
y21• |
y22• |
… |
y2b• |
y2•• |
|
... |
… |
… |
… |
… |
… |
|
i=a |
ya11 |
ya21 |
… |
yab1 |
ya1• |
|
ya12 |
ya22 |
… |
yab2 |
ya2• |
||
… |
… |
… |
… |
… |
||
ya1n |
ya2n |
… |
yabn |
ya•n |
||
суммы |
ya1• |
ya2• |
… |
yab• |
ya•• |
|
суммы |
y•1• |
y•2• |
… |
y•b• |
y••• |
|
|
|
|
|
|
|
|
В таблице приведены наблюдаемые значения целевой функции yijk при изменении фактора х1 на а уровнях (i=1,2,3,…,a), фактора х2 на b уровнях (j=1,2,3,…, b). В каждой точке эксперимента проведено по n повторных опытов (k=1,2,3,...,n). Эксперимент проведен при всех возможных сочетаниях уровней факторов х1 и х2 содержит ab уровней и состоит из abn опытов.
Введем обозначения сумм и средних значений, приняв (•) за символ суммирования по соответствующему индексу:

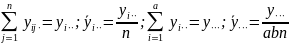
Дисперсионное уравнение двухфакторного эксперимента имеет вид
y=A+b+AB+-e
Общая
дисперсия эксперимента

где ƒобщ = abn - 1 - общее число степеней свободы.
Его можно
представить в виде

в чем легко убедиться, раскрыв скобки.
Каждое
из слагаемых последнего уравнения
представляет собой число степеней
свободы соответствующих факторов, их
взаимодействий и ошибки опыта, т.е.
 (5.1)
(5.1)
Сумма квадратов отклонений
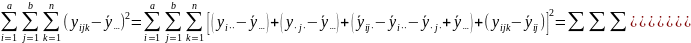
Доказано,
что все удвоенные произведения равны
нулю. Если ввести обозначения суммы
квадратов отклонений
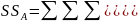

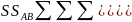
то
получим
 (5.2)
(5.2)
Уравнения (5.1) и (5.2) отражают основные свойства общей дисперсии. Ее числитель и знаменатель можно разложить соответственно на сумму квадратов отклонений и сумму степеней свободы каждого эффекта модели.
Расчет квадратов отклонений удобно проводить по преобразованным формулам, которые сведены в таблице.
Фактор |
f |
SS |
дисперсия , S2 |
X1 |
а-1 |
SSA= |
SA2= |
X2
|
b-1 |
SSA= |
SB2= |
X1 X2 |
(а-1)( b-1) |
SSAB=
|
SAB2=
|
общая дисперсия |
abn-1 |
SSобщ=
|
|
ошибка опыта (воспроизводимости) |
ab(n-1) |
SSош=
|
S2ош=
|
правила выбора ƒ и SS (сумма квадратов отклонений) для любого k.
Для числа степеней свободы ƒ:
1. По
фактору число степеней свободы на
единицу меньше числа уровней по этому
фактору
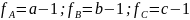 и т.д.
и т.д.
2. Число степеней свободы взаимодействия равно произведению числа степеней свободы взаимодействия факторов
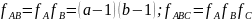
3. Общее число степеней свободы равно общему числу опытов без единицы. При двух факторах, при трех факторах и т.д.
4. Число степеней свободы ошибки ƒош равно числу точек эксперимента, умноженному на (n-1). Для двух факторов ƒош =ab(n-1); для трех факторов - ƒош = abсn(n-1).
Если число опытов в каждой точке неодинаково, то для двух факторов

Для суммы квадратов:
Общая сумма квадратов отклонений равна сумме квадратов отклонений каждого эффекта модели эксперимента. Для k=3 имеем
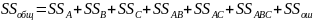
2. Сумма
квадратов эффекта будет содержать такое
же количество членов и с такими же
знаками, что и разложение выражения для
числа степеней свободы
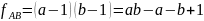
В нашем случае будем иметь четыре члена.
3. Каждый
член суммы квадратов эффекта содержит
количество сумм, равное количеству
параметров в указанном разложении. В
нашем случае первый член разложения
равен αb, поэтому первый член суммы
квадратов имеет
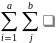 .
Для второго члена
.
Для второго члена
 и
т.д. Последний член не содержит сумм.
и
т.д. Последний член не содержит сумм.
4. Под знаками сумм в числителе записываем у2 c индексами, по которым производится суммирование, заменяя остальные индексы (•) и соответственно выписывая их конечные значения в знаменатель.
Пример:
Для
случая трех факторов: Ф=3,i
= 1,2...,α; j
= 1,2,…,b;
s=1,2,…,c.
Число опытов одинаково для всех факторов
k=1,2,…,n:

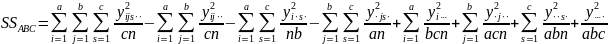

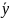 1
1 -
-
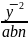

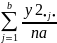 -
-


 –
–
 –
–
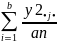 -
-

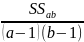
 -
-

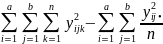
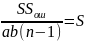 y2
y2