4.3. Вопросы для самопроверки

1. Для чего и в каких случаях применяются методы поиска экстремума?

2. В чем особенность одномерных методов поиска?

3. Перечислите достоинства и недостатки метода дихотомии.

4. Какой из рассмотренных одномерных методов: дихотомии, Фибоначчи или «золотого сечения» наиболее эффективен и почему?

5. Что такое интервал неопределенности?

6. Перечислите основные шаги при поиске экстремума методом Фибоначчи.

7. Для чего необходимо рассчитывать количество экспериментальных точек при использовании одномерных методов?

8. В чес сходство и в чем различие методов дихотомии, Фибоначчи и «золотого сечения»?

9. Зачем требуется определять минимальную длину интервала неопределенности?

10. Чем определяется эффективность метода поиска экстремума?

11. От чего зависит длина интервала неопределенности?

12. Почему один из методов назван именем Фибоначчи?

13. Когда прекращается поиск в одномерных методах?

14. В чем особенность многомерных методов поиска экстремума?

15. Что такое единичные шаги фактора?

16. Что общего и в чем различие межу методами Гаусса-Зайделя, МКВ и симплекса?

17. Какой из методов: Гаусса-Зайделя, MKB или симплекса наиболее эффективен и почему?

18. Когда целесообразно применять метод Гаусса-Зайделя и почему?

19. Какие из многомерных методов наиболее доступны программированию? Обоснуйте свой ответ.

20. Когда заканчивается поиск в методах Гаусса-Зайделя, MKB и симплекса?

21. Какие параметры управляют точностью поиска в симплекс-методе?

22. Какие требования к объекту исследования должны выполняться при использовании многомерных методов поиска?

23. Что такое симплекс? В чем сущность симплекс-метода?

24. Чем руководствуются при выборе шага фактора при поиске экстремума?

25. Можно ли менять величину шага фактора при поиске экстремума методами Гаусса-Зайделя и МКВ?

26. В чем сущность метода крутого восхождения?

27. Для каких типов математических моделей применим МКВ?

28. Дайте определение градиента функции.

29. Как выбрать базовый фактор?

30. Как рассчитать единичные шаги факторов?

31. Как спланировать серию мысленных опытов при поиске максимума?

32. Как реализовать серию мысленных опытов?

33. Когда применение метода MKB эффективно?

34. Перечислите достоинства МКВ.

35. В чем заключается идея метода Гаусса-Зайделя?

4.4. Задачи и упражнения к разделу

1. Определить значение х_опт, при котором целевая функция Y=5·10² - (х-7·Ф)² принимает максимальное значение на интервале[0,1000]. Ф - число букв в фамилии студента. Положение экстремума определить с погрешностью ε=0,05 и точностью измерений δ=20.

2. При реализации ДФЭ 2^6-3 была получена линейная модель вида Y=0,856-0,181 х₂ -0,156х₃ + 0,119х₄. Факторы х₁,х₅,х₆ – незначимые. Используя MKB, найдите минимальное значение целевой функции. О факторах также известны следующие данные:

Факторы	X1	X2	X3	X4	X5	X6
Основной уровень	1000	20	0,05	25	15	3
Интервал варьирования	50	10	0,25	25	5	1

3. Используя симплекс-метод, найти оптимальные значения параметров х₁ и х₂, обеспечивающие минимум целевой функции 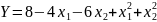, если известны следующие данные о факторах:

Фактор	Основной уровень	Интервал варьирования
X1	200	5Ф
X2	30	3

Начальное положение симплекса описываются следующими точками:

Точка	X1	X2
1	0	0
2	1	0
3	0,5	0,86