3.5. Планы второго порядка

Планы второго порядка обычно применяют в следующих случаях:

а) когда линейная модель неадекватна;

б) после достижения области экстремума для ее описания.

Например, модель второго порядка для k=2 имеет вид

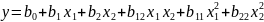
Число членов в этой модели равно

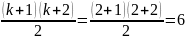
Поэтому число опытов для ее построения N должно быть не меньше, чем

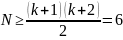
При этом опытов в полном факторном эксперименте ПФЭ 2² не хватает. Чтобы увеличить число опытов, каждый фактор должен принимать не 2 значения, a 3, т.е. необходимо проводить эксперименты N=3^k=9. Применение таких планов связано с большим числом опытов. А мы стремимся к минимизации их числа. При построении планов второго порядка более рациональным является применение ЦКП - центрального композиционного планирования. Эта процедура предполагает реализацию опытов ПФЭ при k<5, или ДФЭ, если k>5. Затем к этим точкам добавляется некоторое количество специально расположенных точек, которые называются «звездными». Для случая двух факторов ЦКП имеет вид:

№ опыта	X0	X1	X2	X1X2	X12	X22	Y	примечание
1	1	-1	-1	1	1	1	Y1	Ядро ПФЭ 2k
2	1	1	-1	-1	1	1	Y2
3	1	-1	1	1	1	1	Y3
4	1	1	1	-1	1	1	Y4
5	1	α	0	0	α2	0	Y5	Звездные точки
6	1	-α	0	0	α2	0	Y6
7	1	0	α	0	0	α2	Y7
8	1	0	-α	0	0	α2	Y8
9	1	0	0	0	0	0	Y9	Основной уровень

Такие планы называются центральными, т.к. все опыты расположены симметрично относительно центра (основного уровня), и композиционными, т.к. строятся они последовательно.

Общее число опытов для ЦКП N=N₁+2k+N₀, где N₁ – число опытов ядра плана, N₁=2^k при k≤5; N₁=2^k-p при k>5; 2k – число «звездных» точек, N₀ – число опытов в центре плана. Для ЦКП N₀=1. Число уровней варьирования каждого фактора составляет 5 (-α;-1;0;1;α).

Построим матрицу планирования ЦКП для случая 3 факторов:

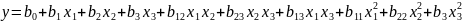
№ опыта	X0	X1	X2	X3	X1X2	X2X3	X1X3	X12	X22	X23	Y	примечание
1	1	-1	-1	-1	1	1	1	1	1	1		Ядро ПФЭ 2k
2	1	1	-1	-1	-1	1	-1	1	1	1
3	1	-1	1	-1	-1	-1	1	1	1	1
4	1	1	1	-1	1	-1	-1	1	1	1
5	1	-1	-1	1	1	-1	-1	1	1	1
6	1	1	1	1	-1	-1	1	1	1	1
7	1	-1	1	1	-1	1	-1	1	1	1
8	1	1	1	1	1	1	1	1	1	1
9	1	α	0	0	0	0	0	α2	0	0		Звездные точки
10	1	-α	0	0	0	0	0	α2	0	0
11	1	0		0	0	0	0	0	α2	0
12	1	0	-α	0	0	0	0	0	α2	0
13	1	0	0	α	0	0	0	0	0	α2
14	1	0	0	-α	0	0	0	0	0	α2
15	1	0	0	0	0	0	0	0	0	0	0	Основной уровень

Число опытов данного ЦКП N=15. При ПФЭ 3³ – N =27. Число опытов уменьшилось в 2 раза.

Заметим, что в матрице ЦКП не все столбцы ортогональны:

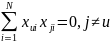
Например,

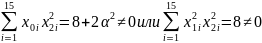
Ортогональность столбцов матрицы можно получить, если ввести новые переменные:

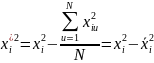
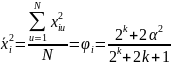
Тогда матрица ЦКП становится ортогональной.

В результате математических преобразований получаем модель в виде:

где

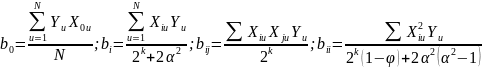
причем α и φ зависят от числа факторов. Их выбирают по таблице.

№	α	ϕ	N	Ядро	№
2	1	0,667	9	Ядро ПФЭ 22	1
3	1,215	0,73	15	Ядро ПФЭ 23	1
4	1,414	0,8	25	Ядро ПФЭ 24	1
5	1,547	0,77	27	Ядро ПФЭ 25	1