2. Магнитное удержание плазмы.

Задача удержания плазмы магнитным полем обычно подразделяется на две отдельные задачи: о равновесии и об устойчивости. Равновесие - это такое состояние, при котором все силы, действующие на систему, компенсируют друг друга. Задача поиска такого состояния обычно рассматривается как статическая, не зависящая от времени.

Равновесное состояние может быть устойчивым или неустойчивым. Анализ устойчивости равновесия обычно проводится с помощью введения малого возмущения: если возмущение нарастает во времени - система неустойчива, если оно затухает - устойчива.

1. Равновесие плазмы в магнитном поле

2.1.1. Принцип равновесия

Чтобы плазма находилась в равновесии в магнитном поле, необходимо уравнивание сил газодинамического и магнитного давлений. Рассмотрение будем вести в приближении одножидкостной гидродинамики. Условие равновесия должно получиться из уравнения движения проводящей жидкости :

(2.1)

где , ;

;

;

.

При это дает

(2.2)

Используя одно из уравнений Максвелла :

и пренебрегая ввиду относительной медленности процессов токами смещения :

(1/c) E/t 0 , преобразуем левую часть соотношения (2.2)

(2.3)

Дальнейшее преобразование удобно произвести используя следующее соотношение :

(2.4)

где - радиус кривизны силовой линии магнитного поля. Второе слагаемое в

(2.3) преобразуется :

(2.5)

где ; - проекция градиента на направление магнитного поля . Подставляя теперь (2.5) в (2.3) получаем для электродинамической силы :

(2.6)

Первое слагаемое здесь представляет уже известный нам градиент магнитного давления, а второе учитывает силу, вызываемую «натяжением » силовых линий. Подставив полученное выражение в выписанное выше условие равновесия (2.2), имеем:

(2.7)

При однородном магнитном поле силовые линии прямые и уравнение

(2.7) сводится к

, т.е. (2.8)

В частности, для случая резкой границы плазмы :

(2.9)

B₀ - вакуумное магнитное поле.

Полученные результаты справедливы для описания равновесия границы плазмы в любом случае.

2.1.2. Плазменный шнур с током

Рассмотрим конкретный случай равновесия, при котором магнитное поле, удерживающее плазму, создается током, протекающим по плазменному шнуру. Это так называемый Z - пинч.

Пусть имеется цилиндрически симметричный плазменный шнур, вдоль которого течет ток. Будем считать, что плотность тока и другие параметры плазмы зависят только от радиуса :

,

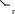
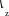
Магнитное поле при этом имеет только азимутальную составляющую

Связь магнитного поля с плотностью тока берем из уравнений Максвелла

(2.10)

или, с учетом цилиндрической симметрии :

(2.10а)

Интегрируя плотность тока в шнуре по всему сечению, получаем полный ток разряда :

где а - радиус плазменного столба. Из этого равенства выражаем магнитное поле на границе шнура :

(2.1.2.2 11)

При r  a , то-есть там, где j = 0 , поле спадает обратно пропорционально радиусу : B  1/r {Это следует из2.1.2.1а : при j = 0 , т.е. , что дает нам хорошо известную формулу для магнитного поля линейного тока :

(2.1.2.3 12)

Таким образом условие равновесия (2.11) для рассматриваемого случая запишется так :

(2.1.2.4 13)

или это может быть преобразовано к виду :

(2.1.2.5 14)

Умножив обе части (2.13) на r² и интегрируя по радиусу от 0 до a , получим интегральное условие равновесия :

- r² dr = a² B² ( a) (2.1.2.6 15)

Интеграл в левой части (2.15) берется по частям :

- r² dr = - 2 = -  p  a² (2.1.2.7 16)

 = fφ - ; f= r² , d φ = dp 

•  p  = { } / - среднее по сечению давление 

Подставив результат интегрирования в (2.1.2.6 15) , получаем интегральное условие равновесия

 p  = B² ( a ) (2.1.2.8 17)

или, выразив с помощью (2.11) B через полный ток :

 p  = (2.1.2.9 18)

Если температуры электронов и ионов постоянны по сечению шнура, то, с учетом того, что p = n(T_e + T_i ) , (2.18) можно представить как

I² = 2 c² (T_e + T_i ) N (2.1.2.10 19)

Здесь N =  a ²  n  - линейная плотность плазмы - число частиц на единицу длины столба. Итак, выражения (2.17), (2.18) и (2.19) являются интегральными условиями равновесия Z - пинча.

Эти условия легко могут быть обобщены на случай , когда плазменный шнур с током находится в продольном магнитном поле. Условие равновесия в этом случае будет выглядеть следующим образом :

= - [ B[ B ]]_r = - ( B_ r ) - B_z (2.1.2.11 20)

или, объединив слева «градиентные» члены :

( p + ) = - ( B_ r ) (2.1.2.12 21)

что совпадает с (2.13) с точностью до замены p на ( p + ) . Далее поступаем с уравнением (2.21) так же, как с (2.13) : умножаем на r² обе части и интегрируем по радиусу. Получаем интегральное условие равновесия для рассматриваемого случая :

 p  = - = - (2.1.2.13 22)

Здесь - усреднение по сечению плазмы, как и для  p . Учтено также, что при r = a B_zin = B_zex .

2.1.3. Равновесие тороидального плазменного шнура с током.

Будем вначале считать тороидальность слабой : a << R и поле тока, текущего по плазме, сравнительно небольшим : B_  B_ . При этом уравнение равновесия ( ) можно разложить в ряд по малому параметру ( a/R ) . В нулевом приближении ( a/R = 0 ) тороидальный шнур становится цилиндрическим и условие равновесия нам известно из рассмотрения предыдущего параграфа : соотношение (2.22) с точностью до обозначений :

< p > = + = + ( 2.1.3.1 33)

Равенство (2.33) называют условием равновесия «по малому радиусу тора».

В следующем приближении учитываются силы, пропорциональные a/R и возникающие из-за тороидальности. Удобно ввести интегральную (по объему плазмы) силу, вызывающую движение по большому радиусу тора. Эту силу можно определить через энергию системы :

F_R = (2.1.3.2 34)

W ( R ) - энергия системы, состоящей из плазмы, магнитного поля тока и тороидального магнитного поля. «Плазменная составляющая» определяется средним по объему газокинетическим давлением

W_p = = 2 ² a² R < p > (2.1.3.3 35)

Энергия витка с током может быть выражена через индуктивность витка :

W_I = L I² (2.1.3.4 36)

Индуктивность можно рассчитывать по формуле :

L = 4  R ln ( ) - 2 + ; (2.1.3.5 37)

l_i = - внутренняя индуктивность распределенного тока, отнесенная к единице длины шнура.

Внутренняя энергия, запасенная в продольном магнитном поле может быть подсчитана интегрированием плотности магнитной энергии как по «внутреннему» ( V_in ) объему плазмы так и по внешнему пространству ( V_ex ) :

W_B = dV + dV = dV + dV =

= dU + 2² a² R . (2.1.3.6 38)

Суммируя (2.35), (2.36) и (2.38) и взяв производную по R, получаем растягивающую центробежную силу :

F_R = 2² a² { < p > - + ( ln - 1 + )} (2.1.3.7 39)

Используем теперь условие равновесия по малому радиусу (2.22). Исключим с его помощью член с разностью внешнего и внутреннего магнитных давлений в (2.39) и получим в результате:

F_R = ( ln - ) (2.40)

Чтобы скомпенсировать эту силу, нужно ввести дополнительное магнитное поле B_z . При однородном поле B_z сила, парирующая центробежную, определится соотношением :

(2.1.3.9 41)

Приравнивая (2.39) и (2.40) , получим требующуюся для равновесия величину B_z :

ln - ) (2.1.3.10 42)

Это условие равновесия «по большому радиусу тора».

Чтобы поддерживать равновесие при изменяющихся параметрах плазмы, необходимо менять B_z. На больших современных токамаках это делается с помощью цифровых автоматических управляющих систем, однако на первых токамаках использовался проводящий кожух. Если проводимость такого кожуха достаточно велика, то наводимые в нем при перемещении плазменного шнура токи создают поле B_z, необходимое для парирования такого смещения. При малой тороидальности равновесное смещение нетрудно оценить аналитически.

Пусть радиус плазмы много меньше радиуса кожуха ( a<<b), который, в свою очередь, много меньше большого радиуса токамака( b<<R). Пусть ось шнура смещена относительно оси камеры на расстояние . Тогда влияние кожуха при b>>a эквивалентно появлению «тока изображения» на расстоянии d = b² / от оси ( это строго справедливо в цилиндре).

Создаваемое токами изображения поле в области шнура равно :

(2.1.3.11 43)

Оно может считаться однородным, поскольку d >>a . При определении условий равновесия следует также учесть, что индуктивность витка с током будет теперь отличаться от даваемой выражением (2.37). Ее величина :

(2.1.3.12 44)

Подставляя в (2.42) выражение для поля (2.43) и учитывая (2.44) получаем окончательно :

(2.1.3.13 45)

Рассмотрение этой задачи без предположения о малости a/b следующий результат :

(2.1.3.14 46)