Учебная дисциплина МАТЕМАТИКА 1.1

Ф ТПУ 7.1-21/01

ЗО Зачёт Курс 1

«

Вариант 1

1. Дана система линейных уравнений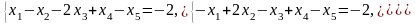

а) Проверьте, совместна ли система.

Если да, то

б) найдите общее решение системы;

в) найдите частное решение системы и сделайте проверку.

2. Даны три вектора 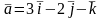, , 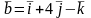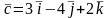. Найдите .

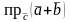3. Составьте уравнение плоскости, которая проходит через точк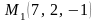и и 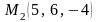параллельно оси Oz.

4. Приведите уравнение кривой к каноническому виду и постройте кривую

.

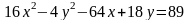5. Постройте поверхность, определяемую уравнением .

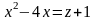Составил Цехановский И.А.

«Утверждаю», зав. кафедрой ВММФ Трифонов А.Ю.

Учебная дисциплина МАТЕМАТИКА 1.1

Ф ТПУ 7.1-21/01

ЗО Зачёт Курс 1

Дата

Вариант 2

1. Дана система однородных линейных уравнений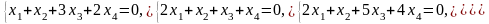

а) Проверьте, имеет ли система нетривиальные решения;

б) Найдите общее решение системы;

в) найдите фундаментальную систему решений.

2. Найдите 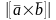, если известно, что , , .

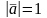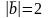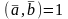3. Составьте уравнение прямой 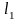, проходящей через точку A(2, 1) под углом 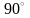к прямой l: 2x + 3y + 4 = 0.

4. Постройте кривую .

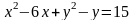5. Постройте поверхность, определяемую уравнением .

.

Составил Цехановский И.А.

«Утверждаю», зав. кафедрой ВММФ Трифонов А.Ю.

Учебная дисциплина МАТЕМАТИКА 1.1

Ф ТПУ 7.1-21/01

ЗО Зачёт Курс 1

Дата

Вариант 3

1. Дана система линейных уравнений

а) Проверьте, совместна ли система.

Если да, то

б) найдите общее решение системы;

в) найдите частное решение системы и сделайте проверку.

2. Вычислите длину вектора 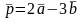, если , .

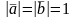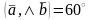3. Плоскость проходит через точку M(6, −10, 1) и отсекает на оси Ox отрезок a = −2, на оси Oz отрезок c = 1. Составьте уравнение этой плоскости.

4. Постройте кривую 4 .

5. Постройте поверхность, заданную уравнением .

.

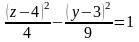Составил Цехановский И.А.

«Утверждаю», зав. кафедрой ВММФ Трифонов А.Ю.

Учебная дисциплина МАТЕМАТИКА 1.1

Ф ТПУ 7.1-21/01

ЗО Зачёт Курс 1

Вариант 4

1. Найдите фундаментальную систему решений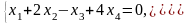

2. Найдите косинус угла между диагональю куба и его ребром.

3. Составьте уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям 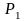: 2x – 2y + z −1 = 0 и плоскостью 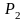: x + 2y +3 z = 0.

4. Приведите уравнение кривой к каноническому виду и постройте кривую

.

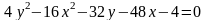5. Постройте поверхность, определяемую уравнением .

.

Составил Цехановский И.А.

«Утверждаю», зав. кафедрой ВММФ Трифонов А.Ю.

Учебная дисциплина МАТЕМАТИКА 1.1

Ф ТПУ 7.1-21/01

ЗО Зачёт Курс 1

Дата

Вариант 5

1. Докажите, что существует единственное значение 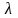, при котором система

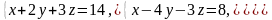совместна. Решите систему при этом значении .

2. Даны векторы 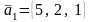, , 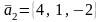, 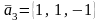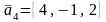Проверить, образуют ли первые три вектора базис, и если да, то разложить четвертый по базису, состоящему из первых трех.

3. Найдите острый угол между плоскостью , проходящей через три точки 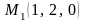, , 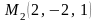и плоскостью xOy.

4. Постройте кривую .

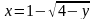5. Постройте поверхность, определяемую уравнением .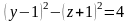

Составил Цехановский И.А.

«Утверждаю», зав. кафедрой ВММФ Трифонов А.Ю.

Учебная дисциплина МАТЕМАТИКА 1.1

Ф ТПУ 7.1-21/01

ЗО Зачёт Курс 1

Вариант 6

1. Дана система линейных уравнений

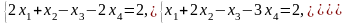
а) Проверьте, совместна ли система.

Если да, то

б) найдите общее решение системы;

в) найдите частное решение системы и сделайте проверку.

2. Найдите косинус угла между прямой x + 4y – 4 = 0 и прямой, проходящей через точк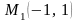и и .

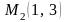3. Составьте уравнение плоскости, проходящей через точку и параллельно плоскости P: x – 2y +3 z + 5 = 0.

4. Постройте кривую .

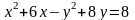5. Постройте поверхность, определяемую уравнением .

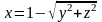Составил Цехановский И.А.

«Утверждаю», зав. кафедрой ВММФ Трифонов А.Ю.

Учебная дисциплина МАТЕМАТИКА 1.1

Ф ТПУ 7.1-21/01

ЗО Зачёт Курс 1

Дата

Вариант 7

1. Дана система линейных уравнений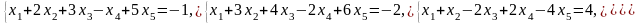

а) Проверьте, совместна ли система.

Если да, то

б) найдите общее решение системы;

в) найдите частное решение системы и сделайте проверку.

2. Найдите высоту AH треугольника с вершинами в точках A(4, 2, 0), B(1, 0, −3), C(2, 2, 6).

3. Найдите острый угол между плоскостью , проходящей через точки 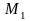(3, 1, 1) 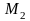(2, −2, 4) 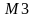(1, −4, 4)и осью Oz.

4. Постройте кривую .

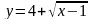5.Постройте поверхность, определяемую уравнением .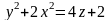

Составил Цехановский И.А.

«Утверждаю», зав. кафедрой ВММФ Трифонов А.Ю.

Учебная дисциплина МАТЕМАТИКА 1.1

Ф ТПУ 7.1-21/01

ЗО Зачёт Курс 1

Вариант 8

1. Дана система линейных уравнений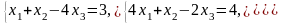

Проверьте, имеет ли система единственное решение, и найдите его.

2. Даны вершины треугольной пирамиды A(0, 2, 0), B(1, 4, −1), C(2, 3, 5), D(6, 0, −3). Найдите объём пирамиды и длину высоты АН.

3. Найти угол между прямым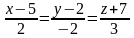и : и :

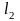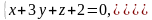
4. Приведите уравнение кривой к каноническому виду и постройте кривую

.

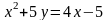5. Постройте поверхность, определяемую уравнением .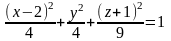

Составил Цехановский И.А.

«Утверждаю», зав. кафедрой ВММФ Трифонов А.Ю.

Учебная дисциплина МАТЕМАТИКА 1.1

Ф ТПУ 7.1-21/01

ЗО Зачёт Курс 1

Дата

Вариант 9

1. Докажите, что векторы 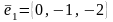, , 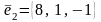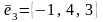можно принять за новый базис и найдите координаты вектора 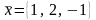в этом базисе.

2. Дан определитель .

а) Запишите разложение определителя по элементам второй строки, не вычисля его;

в) вычислите определитель, предварительно получив нули в какой-либо строке или столбце.

3. При каком значении параметра 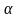прямая l: 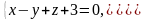параллельна плоскости P: 2x – y + αz – 2 = 0 или принадлежит ей?

4. Приведите уравнение кривой к каноническому виду и постройте её .

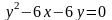5. Постройте поверхность, заданную уравнением .

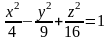Составил Цехановский И.А.

«Утверждаю», зав. кафедрой ВММФ Трифонов А.Ю.

Учебная дисциплина МАТЕМАТИКА 1.1

Ф ТПУ 7.1-21/01

ЗО Зачёт Курс 1

Дата

Вариант 10

1. Дана система линейных уравнений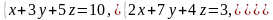

Решите систему матричным методом и сделайте проверку

2. Найдите объем тетраэдра, построенного на векторах , , .

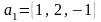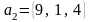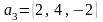3. Найдите проекцию точки A(2, –1, 3) на прямую x = 2t, y = t – 1, z = 2t - 2.

4. Постройте кривую .

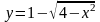5. Постройте поверхность, определяемую уравнением .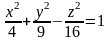

Составил Цехановский И.А.

«Утверждаю», зав. кафедрой ВММФ Трифонов А.Ю.

Учебная дисциплина МАТЕМАТИКА 1.1

Ф ТПУ 7.1-21/01