8. В чем заключается контроль правильности вычисления дирекционных углов сторон замкну-того теодолитного хода?
Контроль вычисления дирекционных углов: в замкнутом теодолитном ходе в результате вычислений получается дирекционный угол исходной стороны.
9. Какова сущность прямой и обратной геодезических задач?
Сущность прямой геодезической задачи состоит в том, что по координатам исходной точки А и полярному углу α направления АВ, требуется определить координаты другой точки В. Так как в практике прямоугольные координаты не измеряют, то для решения задачи измеряют полярный угол α и расстояние d (рис.23).
Рисунок 23
Для выноса проекта на местность бывает необходимо по данным прямоугольных координат найти значение дирекционного угла и длину линии между заданными точками. Это и составляет сущность решения обратной геодезической задачи.
10. Какие знаки имеют приращения в зависимости от названия румбов их сторон?
Знаки приращений координат δX и Δy
Используя зависимость между дирекционными углами и осевыми румбами (рис. 11), находим альфа AB
Рис. 11. Осевые румбы и дирекционные углы
Зависимость между дирекционными углами и румбами определяется для четвертей по следующим формулам:
I четверть (СВ) r = альфа,
II четверть (ЮВ) r = 180° – альфа,
III четверть (ЮЗ) r = альфа – 180°,
IV четверть (СЗ) r = 360° – альфа.
Расстояние SAB определяем по формуле:
Для контроля расстояние SAB вычисляют дважды по формулам:
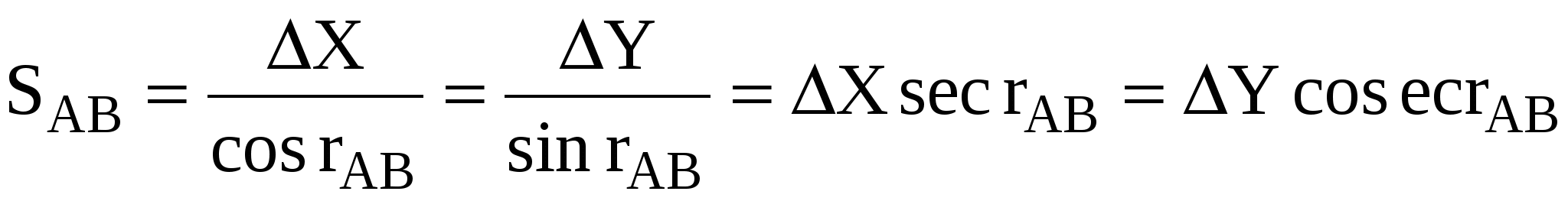
11. Как вычисляются невязки в приращениях координат замкнутого теодолитного хода, их допустимость и распределение?
Из геометрии известно, что сумма проекций сторон многоугольника на любую ось равна нулю, следовательно:
Под влиянием ошибок измерений замкнутый полигон будет разомкнутым на величину fр – абсолютная невязка в периметре полигона.
Если полученная невязка недопустима, то необходимо произвести повторное измерение длин линий. Если невязки допустимы, то они распределяются на приращения координат пропорционально длинам сторон с противоположным знаком, то есть сумма исправленных приращений должна быть точно равна теоретической сумме – в данном случае равна нулю. Координаты вершин хода:
12. Чему равна сумма исправленных приращений координат в замкнутом теодолитном ходе?
Если невязки допустимы, то они распределяются на приращения координат пропорционально длинам сторон с противоположным знаком, то есть сумма исправленных приращений должна быть точно равна теоретической сумме.
13. Как вычисляются и контролируются координаты вершин замкнутого теодолитного хода?
По исправленным приращениям координат от точки с известными координатами последовательно вычисляют координаты вершин теодолитного хода, используя формулы прямой геодезической задачи:
Xпосл = Хпред + ΔХисп;
Yпосл = Yпред + ΔYиспр.
Контролем правильности вычислений является получение координат исходной (начальной) точки (Х1, Y1) замкнутого теодолитного хода.
14. Как строится координатная сетка и как контролируется правильность ее построения?
Координатную сетку можно построить с помощью линейки поперечного масштаба. Рассчитайте количество квадратов по осям х и у. Пусть согласно заполненной ведомости вычисления координат требуется составить план в масштабе 1:5000. При этом длина стороны квадрата сетки (5 см) соответствует 250 м горизонтального проложения местности. Исходя из значений координат хода, определяем величины:
где Хmax , Уmax – максимальные значения координат точек, округленные в большую сторону до величин, кратных длине квадрата сетки в данном масштабе; Xmin , Ymin– минимальные значения координат, округленные в меньшую сторону до величин, кратных длине квадрата сетки в данном масштабе.
Рисунок 7
Постройте сетку квадратов, для этого на листе бумаги проведите диагонали АВ и CD. Из точки пересечения диагоналей (точки 0) сделайте циркулем засечки одинакового размера. Полученные точки а, d, b и с соедините прямыми линиями. Стороны прямоугольника асbd разделите пополам и через точки деления проведите прямые 1–2 и 3–4, которые должны пройти через точку 0 пересечения диагоналей. Если число квадратов четное, то от нуля в направлении точек 1, 2, 3 и 4 отложите отрезки, равные стороне квадрата сетки. При нечетном числе квадратов от нуля откладывают сначала половину стороны квадрата сетки, а затем величину, равную стороне квадрата сетки. Соединив линиями соответствующие точки на противоположных сторонах прямоугольника, получают сетку квадратов. Циркулем-измерителем проверьте правильность построения координатной сетки путем измерения диагоналей ее квадратов; длины диагоналей должны быть равны 7,07 см или отличаться от этой величины не более чем на ± 0,2 мм.