Основные определения и законы для контрольной

Сложная задача – это задача, которая не может быть эффективно решена на существующих массовых вычислительных средствах с помощью традиционных методов и алгоритмов решения.

Ускорение

Эффективность

Цена параллельного решения

Ценность

Коэффициент загрузки процессора

Коэффициент простоя процессора

Загруженность

Связь загруженности и эффективности

Лемма Брента.

Если при неограниченном числе процессоров для вычисления арифметического выражения, содержащего операций, требуется время , то при наличии ограниченного числа процессоров вычисление может быть выполнено не более чем за время , определяемое по формуле:

Закон Амдаля.

Используется для оценки параллельных алгоритмов, структура которых предполагает выполнение всех операций либо с максимальной, либо с минимальной степенью параллелизма, время на подготовку передачи данных отсутствует.

Оценка ускорения, которое может быть получено на компьютере из процессоров при данном значении (доля операций, которые нужно выполнять последовательно, ):

1. 

2. 

3. 

Следствие из закона Амдаля.

Для того чтобы ускорить выполнение программы в раз, необходимо ускорить не менее чем в -ую часть программы.

– время выполнения узлов графа;

– время передачи данных.

1. Слабосвязанные задачи

2. Среднесвязанные задачи

3. Сильносвязанные задачи

Алгоритм определения критического пути:

1. При начальном проходе определяется минимально возможное время начала выполнения каждого узла по формуле:

где – число узлов-предшественников i-ого узла;

– минимально возможное время начала выполнения i-ого (j-ого) узла;

– время выполнения j-ого узла;

– время передачи данных между i и j узлами.

2. При повторном проходе (от конечной вершины к начальной) определяется максимально возможное время начала выполнения каждого узла по формуле:

где – число узлов-последователей i-ого узла;

– номер конечной вершины графа;

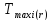– максимально возможное время начала выполнения i-ого (r-ого) узла;

– время выполнения -ого узла;

– время передачи данных между i и r узлами.

3. Определяются критические пути графа в соответствии с правилом: -ый узел является критическим, если выполняется равенство . Критическим путём графа является множество последовательных узлов, у которых .

В случае МВС с общей памятью времена передачи данных удваиваются.

Задача назначения.

Под решением задачи назначения понимается процесс распределения узлов графа задачи (набора задач), выполняемой в МВС, между ее процессорами, при котором определяется время начала выполнения узла, его длительность и назначение процессора, который обеспечит это выполнение.

Известные стратегии назначения готовых к исполнению узлов:

1. равновероятный выбор;

2. выбор узла с минимальным временем выполнения;

3. выбор узла с максимальным временем выполнения;

4. выбор узла, принадлежащего критическому пути;

5. выбор узла, имеющего наибольшее число связей с последующими узлами;

6. выбор узла в порядке поступления в очередь на исполнение.