2.2 Джерела похибки оцінювання частоти

Оцінка частоти 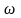по положенню максимуму спектра (1.1) сигналу є найбільш природною. Суворого аналітичного вирішення цього завдання в літературі немає.

Похибка оцінювання, що виникає в ідеальних умовах отримання та обробки сигналу, притаманна кожному методу, називається методичної [35]. Відповідно з цим визначенням методичними будуть похибки визначення частоти і амплітуди відрізка гармонійного сигналу, викликані тільки викривляючим впливом бічних пелюсток спектра і його кінцевої шириною. Аналогічно можна вважати, що при визначенні частот і амплітуд відрізка сигналу, що містить кілька гармонійних доданків, методичними будуть похибки через кінцеву ширину спектра та впливу бічних пелюсток , властивих ПФ при будь-яких способах зважування сигналу. Такому визначенню відповідає, наприклад, відсутність методичної похибки при визначенні частот відрізка гармонійних доданків сигналу при параметричних методах визначення частоти, коли порівнюється сигнал з еталонною копією.

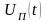Крім методичної, очевидними і відомими причинами виникнення похибки оцінювання є шуми передавача і перших каскадів приймача , наявність перешкод в прийнятому сигналі і похибка визначення тривалості сигналу і,відповідно,меж інтегрування при обчисленні СП. Очевидно, що всі перераховані джерела похибки є незалежними, тому відносну дисперсію загальної похибки оцінювання 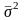можна записати в звичному вигляді (2.4):

, (2.4)

де, відповідно, відносні дисперсії результату оцінювання, викликані методичної похибкою, наявністю шумів, перешкод, дисперсії швидкості поширення електромагнітної хвилі і похибки визначення тривалості сигналу.

У більшості радіотехнічних завданнях спектральний аналіз сигналу виконується після проходження його по яких-небудь ланцюгах і каналах зв'язку , в яких дисперсія швидкості поширення сигналів може бути визначена заздалегідь і врахована при оцінці частоти. Тривалість сигналу можна також вважати апріорно відомою , а похибка її визначення може бути зроблена досить малої і тому далі ці складові похибки не розглядаються.

Найбільш важливими для більшості завдань є перша, друга і третя складові похибки .

2.3 Оцінка похибки визначення

Відповідно до визначення (2.5) для оцінки частоти сигналу необхідно розв’язати рівняння

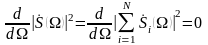, (2.5)

спектральна щільність 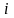-го компонента зваженої вибірки сигналу, отриманого на симетричному часовому інтервалі; 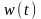- ВФ, симетрична відносно середини вибірки сигналу; - амплітуда і фаза - го компонента сигналу.

Враховуючи теорему зсуву можна стверджувати, що результати, отримані для симетричного тимчасового інтервалу, будуть справедливі для несиметричного тимчасового інтервалу з урахуванням зміни фази.

Ця похибка виникає внаслідок часткового проходження сигналів з одного каналу в інший. Такий небажаний перехресний вплив вхідних сигналів один на одний утворюється завдяки існуванню паразитних ємносних та ідуктивних зв’язків між ланцюгами каналів. Механізм виникнення цієї похибки пояснює структурна схема. В фазовимірювальній апаратурі жорсткі вимоги висуваються до вхідних опорів та їх довгострокової стабільності. Чому? Справа в тому, що повний опір вхідних ланцюгів фазометрів містить і активну, і ємнісну складові, які утворюють фазообертачі. За рахунок їхньої дії у досліджувані сигнали вноситься додатковий неконтрольований фазовий зсув. З метою кількісної оцінки цієї похибки розглянемо вхідний ланцюг фазометра (рис.12.2). На цьому рисунку вхідний опір фазометра представлено паралельно підключеними активним резистором та ємністю. Неважко показати, що додатковий фазовий зсув, обумовлений вхідною ємністю фазометра.

Введемо формовки частоти -го компонента сигналу; та поточної

частоти.

З урахуванням введених позначень представимо розгорнутий запис рівняння

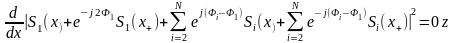
де 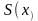та 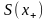- модулі доданків спектральної щільності з негативною і позитивною областей частот, аргументами яких є, відповідно, частоти .

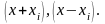Будемо вважати , що відповідає сигналу , частоту якого потрібно визначити .

Отримати загальне рішення рівняння (1.6) не представляється можливим. Однак найчастіше не потрібно знати точну залежність похибки оцінки частоти. Зазвичай найбільш важливими є оцінка максимальних і мінімальних значень цієї похибки і їх положень на шкалі частоти, тому що, саме ці величини визначають метрологічні характеристики радіотехнічної системи, а також визначення умов зниження похибки.

З безлічі рішень рівняння (1.6) представляють інтерес точні рішення, відповідні відсутності похибки, які можуть бути отримані при рівності нулю кожного з доданків (2.6)

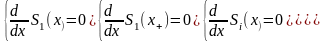
(2.6)

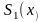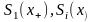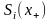Сукупність рішень , обумовлена ​​системою рівнянь (2.6) , відповідає значенням частот , при яких збігаються положення максимуму основної пелюстки доданка спектра з положеннями екстремумів бічних пелюсток доданків та . Слід зазначити важливий факт , що в цьому випадку частота 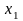для будь-якої застосовуваної ВФ оцінюється без похибки незалежно від фаз доданків сигналу.

Існування точних рішень дозволяє отримати і протестувати наближені рішення рівняння , тому надалі слід виділити всі точні рішення рівняння ( 2.6), у тому числі для приватних випадків .

Для отримання наближених рішень рівняння (1.6) проаналізуємо можливість використання відомої методики отримання наближених рішень аналогічних трансцендентних рівнянь. Враховуючи диференціальність квадрата модуля СП реальних сигналів, розкладемо функцію 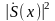в межах точки х , в ряд Тейлора . Використання 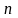- го ступеня розкладання дозволяє наближено представити рівняння алгебраїчним рівнянням ступеня 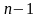. Ступінь допустимого обмеження числа членів ряду можна оцінити співставленням між собою рішень, одержуваних при апроксимації функції різним числом членів ряду, а також порівнянням цих рішень із знайденими точними рішеннями в областях їх існування і з результатами чисельного моделювання. Слід також врахувати, що загальне рішення алгебраїчних рівнянь можна отримати тільки для невисоких ступенів [ 22 ] . У цьому зв'язку "конструкції" наближених рішень повинні адекватно відображати залежності похибок при мінімально допустимому ступені рівняння.

Обмежуючись в розкладанні квадратичним наближенням отримаємо перший наближене рішення рівняння (2.7 ) і, відповідно, похибка

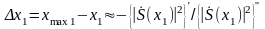. (2.7)

Кубічна апроксимація функції 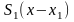и 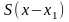дає другий приблизний розв’язок

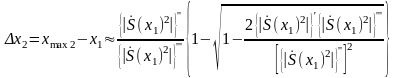. (2.8)

Детальний аналіз рішень (2.8), (2.7) проведемо для обмеженої вибірки моногармонічного сигналу і для бігармонічного сигналу, частоти компонент якого дозволяють знехтувати доданками спектра 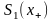і . Для цих випадків у результаті перетворення рівняння (2.6) отримаємо рівняння, одне з яких визначає сукупність точних рішень, що залежать від фазових співвідношень компонент сигналу:

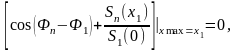(2.9)

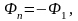
Де для отримання загальних записів двох випадків позначено 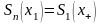- для обмеженої вибірки моногармонічного сигналу і - для бігармонічного сигналу.

У першому з розглянутих випадків, для обмеженої вибірки моногармонічного сигналу, крім рівнянь (2.7), (2.9), що визначають точні рішення, рівняння (1.6) повинно мати точне рішення 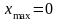для сукупності частот, в яких при виконанні рівності 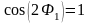основні пелюстки 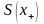і 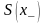не дозволяються. Отже, для всіх ВФ зазначена сукупність точок повинна лежати на прямій

(2.10)

в інтервалі вирішення пелюсток і , який при визначається системою рівнянь:

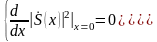(2.11)

У другому випадку використовуючи результати [24, 34], отримуємо, що для бігармонічного сигналу рівняння (1.6), крім сукупностей рішень (2.7), (2.9), має мати точне рішення

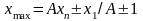при 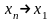(2.12)

.Якщо використання відомої методики отримання наближених рішень трансцендентних рівнянь справедливо, то рішення (2.8), (2.9) у приватному випадку має задовольняти наближеного рішення для огинають максимальних значень похибки, рівняння для яких виходять з (2.5)

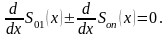(2.13)

Перші і другі приблизні розв’язання рівнянь (2.13) приймають, відповідно, вигляд

:

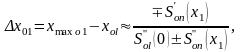(2.14)

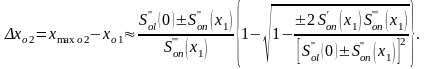(2.15)

Розбіжність отриманих рішень (2.8), (2.9) і (2.15), (2.15) приводить до необхідності корекції отриманих наближених рішень (2.8), (2.9). Враховуючи сукупності точних рішень (2.7), (2.10), (2.11), (2.13) для аналізованого випадку двох доданків у рівнянні (2.6), перше наближене рішення (2.8) виключенням з його знаменника доданка можна привести до виду.

Зрозуміло, виключення одного з доданків у рішенні (2.8), для задоволення його в окремому випадку рішенням (2.15), вимагає детального тестування отриманих наближених рішень, і зіставлення їх з рішенням (2.8), (2.9), отриманими за відомою методикою, яке проведемо далі.

Друге наближення висловимо через перше наближення і поправочний коефіцієнт

де 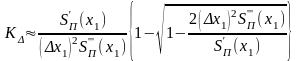(2.16)

При розв’язки (2.15) та (2.16) тотожні, відповідно, розв’язкам.

Зауважимо , що ліві частини виразів збігаються з співмножниками чисельника виразу. З цього випливає, що умови, при яких частота обчислюється без похибки, визначаються виразами для будь-яких ВФ і для будь-яких частот. У такому випадку найбільш значущим залишається питання про ступінь наближення рішень, рівняння до точних значень похибки , який розглянемо нижче на прикладі ВФ Кайзера – Бесселя (КБ) і Дольфа - Чебишева ( ДЧ ), широко використовуються в різних практичних додатках і мають безсумнівний теоретичний інтерес. Теоретичний інтерес до зазначених ВФ обумовлений тим , що їх форма , а значить і форма їх СЩ , обумовлена ​​видом основного і рівнем бічних пелюсток, варіюються одним параметром, що дозволяє досить легко зв'язати їх з похибкою оцінки частоти .