12) Частотная характеристика систем автоматического управления

Если подать на вход системы с передаточной функцией W(p) гармонический сигнал

,

то после завершения переходного процесса на выходе установятся гармонические колебания

с той же частотой, но иными амплитудой и фазой, зависящими от частоты возмущающего воздействия. По ним можно судить о динамических свойствах системы. Зависимости, связывающие амплитуду и фазу выходного сигнала с частотой входного сигнала, называются частотными характеристиками (ЧХ). Анализ ЧХ системы с целью исследования ее динамических свойств называется частотным анализом.

Подставим выражения для u(t) и y(t) в уравнение динамики

(aоpⁿ + a₁pn - 1 + a₂p^{n - 2} + ... + a_n)y = (bоp^m + b₁p^m-1 + ... + b_m)u.

Учтем, что

,

а, значит,

pnu = pnU_mejwt = U_m (jw)nejwt = (jw)nu.

Аналогичные соотношения можно записать и для левой части уравнения. Получим:

По аналогии с передаточной функцией можно записать:

W(j ), равная отношению выходного сигнала к входному при изменении входного сигнала по гармоническому закону, называется частотной передаточной функцией. Легко заметить, что она может быть получена путем простой замены p на j в выражении W(p).

13) Характеристики усиленного звена

Усилительное звено реализует без опоздания следующий закон  , где   - коэффициент передачи или коэффициент усиления. Она также называется безинерционной и пропорциональной.

W(p)=k

k>1 усиливает в k раз.

k<1ослабляет в k раз.

14) Характеристики апериодического звена

15) Характеристики астатического звена

Идеальное интегрируемое звено (астатическое звено) – это звено, которое реализует закон  , где   - коэффициент передачи интегрируемого звена.

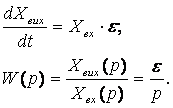
16) Характеристики дифференциального звена

Дифференциальное звено(Идеальное) реализует следующий закон  . Где   - стала дифференцирование. Это звено также имеет название нивки опережения.

Получим передаточную функцию:

17) Характеристики реального дифференциального звена

Передаточная функция

18) Характеристики колебательного звена

Колебательное звено является элементарным динамическим звеном второго порядка, обладает тремя варьируемыми параметрами. Поэтому его характеристикам уделим более пристальное внимание. Тем более, что колебательным звеном описываются достаточно сложные элементы электромеханических систем и электроприводов, на пример, такой распространенный элемент как электродвигатель постоянного тока.

Передаточная функция колебательного звена –

где   – коэффициент усиления,   – постоянная времени,   – коэффициент затухания.

19) Характеристики запаздывающего звена

Запаздывающее звено имеет переходную характеристику

Следовательно, выходной сигнал запаздывающего звена повторяет входной сигнал, но позже на время запаздывания. Исходя из этого, можно записать общее уравнение взаимосвязи входного и выходного сигналов запаздывающего звена в динамическом режиме работы:

X_вх(Τ) = X_вых(Τ + Τ_о) .

20) Пропорциональный закон регулирования

Реализует следующую зависимость:

,

где u - исходная величина;

 - параметр регулятора, коэффициент усиления;

 - входная величина регулятора.

В динамическом отношении такой регулятор является пропорциональным звеном и все что раньше касалось этого звена можно использовать для этого регулятора.

Схема работает следующим чином – если за любой причиной напряжение на выходе генератору возрастает или уменьшается то ток, который проходит через соленоид, увеличивается тяговое усилие соленоида и плунжер смещается кверху, увеличивается сопротивление в кругу обмотки возбуждения (ОЗ на рисунке 2.60). Ток в обмотке возбуждения уменьшается, а значит уменьшается напряжение на выходе генератора. Устойчивый режим наступит тогда, когда тяговое усилие соленоида уравняется с силой деформации пружины.