1.3. Задачи для самостоятельного решения
Вычислить следующие неопределенные интегралы:
1)
,
2)
,
3)
,
4)
,
5)
,
6)
.
1.4. Замена переменной в неопределенном интеграле
Пусть
требуется найти интеграл
.
Сделаем замену переменной в подынтегральном
выражении, положив
,
где
– непрерывная функция с непрерывной
производной, имеющая обратную функцию
.
Тогда
и имеет место следующее равенство
.
Здесь
подразумевается, что после интегрирования
в правой части равенства
нужно
будет вернуться
от
переменной t
к переменной
.
Замечание.
При интегрировании иногда целесообразнее
подбирать замену переменного не в виде
,
а
в
виде
.
Проиллюстрируем это на примере. Пусть
нужно вычислить интеграл, имеющий вид
Здесь
удобно положить
тогда
.
Приведем несколько примеров на интегрирование с помощью замены переменных.
Пример.
Найти интеграл
.
Решение.
Сделаем подстановку
,
тогда
,
следовательно,
.
Пример.
Вычислить интеграл
.
Решение.
Сделаем замену
,
тогда
и интеграл примет вид:
1.5. Задачи для самостоятельного решения
Вычислить неопределенные интегралы с помощью подходящей замены:
1)
2)
3)
4)
5)
6)
1.6. Интегрирование по частям в неопределенном интеграле
Пусть
– непрерывно дифференцируемые функции.
Тогда
.
Интегрируя это равенство, получим
или
.
Эта
формула называется формулой
интегрирования по частям.
Интегрирование по частям состоит в том,
что подынтегральное выражение заданного
интеграла представляется в виде
произведения двух сомножителей
и
(это, как правило, можно осуществить
несколькими способами); затем, после
нахождения
и
,
используется формула интегрирования
по частям.
Укажем некоторые типы интегралов, которые удобно вычислять по частям.
1)
,
,
,
где
– многочлен. В этих интегралах
полагают
.
2)
,
,
,
,
,
где
– многочлен. Здесь, в качестве функции
нужно взять логарифм или обратные
тригонометрические функции.
3)
Интегралы вида
,
вычисляются двукратным интегрированием
по частям.
Пример.
Вычислить интеграл
.
Решение.
Пусть
,
тогда
и, значит,
.
Так как
,
то по формуле интегрирования по частям
имеем:
.
Пример.
Вычислить интеграл
.
Решение.
Пусть
,
тогда
.
Поэтому
,
По формуле интегрирования по частям
имеем:
=
.
В
последнем интеграле делаем замену
,
и получаем:
=
=
=
.
Пример.
Вычислить
интеграл
.
Решение.
Полагаем
.
Тогда
,
и по формуле интегрирования по частям
имеем:
=
=(еще
раз интегрируем по частям, снова полагаем
,
значит
,
)=
=
+
.
Перенося последний интеграл в левую часть, получим:
=
(
+
)
+ С.
1.7. Задачи для самостоятельного решения
Применяя формулу интегрирования по частям, найти интегралы:
1)
2)
3)
4)
5)
6)
1.8. Интегрирование рациональных дробей
Рациональные дроби вида
1)
2)
3)
4)
,
где
и дискриминант многочлена
отрицателен, называются простейшими
рациональными дробями 1, 2, 3 и 4 типов.
Найдем интегралы от простейших рациональных дробей 1–3 типов.
1)
(по таблице интегралов).
2)
(замена
,
)
=
=
3)
=
(выделим в знаменателе полный квадрат)
=
.
Заметим,
что
(дискриминант). Положим
и
сделаем подстановку
Интеграл примет вид:
=
=
.
Возвращаясь
к переменной
,
получаем ответ:
.
Известно,
что произвольный многочлен
может разлагаться на множители двух
видов:
,
или
,
,
причем квадратный трехчлен
имеет отрицательный дискриминант (не
разлагается на множители). Строго эта
теорема звучит так:
Теорема.
Всякий
многочлен
степени
с действительными коэффициентами
разлагается на линейные и квадратные
множители с действительными коэффициентами
=
.
При
этом
.
Выражение
называется правильной
дробно-рациональной функцией,
если
– многочлены, причем степень знаменателя
больше степени числителя.
Интегрирование дробно-рациональных функций основано на следующей теореме о разложении:
Теорема. Всякую правильную рациональную дробь , знаменатель которой разложен на множители
=
можно представить единственным образом в виде следующей суммы простейших дробей:
=
+
...
...+
+...
...+
,
где
– некоторые действительные коэффициенты.
Пример
1. Дробь
представима в виде
.
Пример
2. Представим
дробь
в виде суммы простейших дробей.
Решение.
Заметим, что
выражение (
)
разлагается на множители
.
Потому
=
.
Отметим
также, что числитель не влияет на вид
разложения, а будет влиять только на
значения коэффициентов
Таким образом, можно свести вычисление дробно-рациональной функции к вычислению простейших дробей. Для этого необходимо вычислить неопределенные коэффициенты, возникающие при разложении. Они вычисляются методом неопределенных коэффициентов. Продемонстрируем его на следущем примере.
Пример. Пусть имеется разложение
= .
Найти все коэффициенты этого разложения.
Решение.
Приводим правую часть равенства к общему знаменателю:
=
=
=
Затем
сравниваем коэффициенты при одинаковых
степенях
в числителях левой и правой частей.
Получаем систему:
Решая ее, получаем искомые коэффициенты:
Заметим, что неправильную дробно-рациональную функцию можно превратить в сумму многочлена и правильной дроби с помощью деления углом, т.е.
=
,
где
– многочлен,
– правильная дробь.
Пример. Дана неправильная рациональная дробь
=
.
Разделим числитель на знаменатель:
_
|
_
_
_
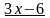
15
Результат деления:
=
+
.
Сформулируем теперь общее правило интегрирования рациональных дробей.
Если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби.
Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей.
Проинтегрировать многочлен и полученную сумму простейших дробей.
Пример
1. Вычислить
.
Решение. Представим подынтегральное выражение в виде
суммы простейших дробей:
=
.
Методом неопределенных коэффициентов находим неизвестные
:
=
=
=
Отсюда
Тогда
=
=
=
+ C.
Пример
2. Вычислить
.
Решение. Дробь неправильная, поэтому делим многочлены углом и выделяем многочлен и правильную дробь
Далее, разложим получившуюся правильную дробь на простейшие дроби
=
Методом неопределенных коэффициентов находим коэффициенты:
Следовательно,
Таким образом,
=
=
+
+
=
.