Программная инженерия. Экзаменационные вопросы по ДМ
.docxЭкзаменационные вопросы по дискретной математике
-
Сети. Потоки в сетях. Теорема Форда – Фалкерсона. Нахождение максимального потока в сети.
-
Функции. Бинарные отношения. Тотальность, сюръективность, инъективность, биективность. Примеры.
-
Бинарные отношения. Свойства. Матрица смежности и граф отношения. Эквивалентные отношения. Примеры.
-
Алгебраические структуры. Полугруппы, моноиды, группы. Примеры.
-
Группы. Абелевы группы, аддитивные, мультипликативные группы. Конечные группы. Таблицы Кэли. Циклические группы. Декартово произведение группы.
-
Группы подстановок. Симметрическая группа
.
Умножение подстановок. Единичный
элемент. Обратная подстановка. Число
элементов группы
. -
Циклы. Теорема о представлении подстановки в виде произведения независимых циклов. Транспозиции. Четные и нечетные подстановки. Знакопеременная группа
. -
Кольца. Свойства колец. Коммутативные кольца. Делители
.
Области целостности. Примеры. Подкольца.
Единица кольца. Поля. Примеры. -
Идеалы. Главные идеалы. Теорема об идеалах поля (только (0) и (1)). Следствие об идеалах в кольце
. -
Сравнения. Классы вычетов по модулю
(по идеалу
).
Свойства сравнений. Малая теорема
Ферма. Функция Эйлера. Теорема Эйлера
(теория чисел). -
Характеристика кольца. Теорема о характеристике кольца без делителей
.
Примеры. Кольца классов вычетов. Примеры. -
Простые идеалы. Необходимое и достаточное условие того, что идеал
кольца
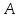— простой. -
Поля классов вычетов. Минимальные поля. Примеры.
-
Евклидовы кольца. Свойства евклидовых колец (8 свойств). Примеры.
-
Кольцо многочленов
.
Условия того, что кольцо
— евклидово кольцо. Примеры. -
Приводимые и неприводимые многочлены в кольце
.
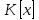Примеры. Теорема о разложении
в
на произведение неприводимых множителей.
Теорема Безу. -
Расширения полей. Теорема о том, что кольцо классов вычетов
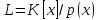по модулю неприводимого многочлена
есть поле. Степень расширения. Число
элементов этого поля. -
Поля Галуа. Примеры полей Галуа, как расширения полей. Таблицы сложения и умножения.