1.6. Показатели, характеризующие тенденцию динамики.

Для того чтобы построить систему показателей, характеризующих тенденцию динамики, нужно подобрать величины, которые характеризуют изменения уровней анализируемого ряда как в абсолютном, так и в относительном вы­ражении. Далее финансового аналитика, как правило, интересует, является ли из­менение временного ряда равномерным или неравномерным, ускоренным или замед­ленным. Наконец, его интересует уравнение тенденции ряда в форме некоторого достаточно простого выражения, наилучшим образом аппроксимирующего фактическую тенденцию динами­ки. Понятие об уравнении тенденции динамики было введено в статистику английским ученым Гукером в 1902 г. Он предло­жил называть такое уравнение трендом (trend).

Для того чтобы нагляднее представить показатели, харак­теризующие тенденцию, следует абстрагироваться от колебле­мости и выявить динамический ряд в форме «чистого» тренда при отсутствии колебаний. Пример такого ряда представлен в табл. 1.4.

Абсолютное изменение уровней - в данном случае его можно назвать абсолютным приростом - это разность между сравни­ваемым уровнем и уровнем более раннего периода, принятым за базу сравнения. Если эта база - непосредственно предыду­щий уровень, показатель называют цепным, если за базу взят, например, начальный уровень, показатель называют базисным. Формулы абсолютного изменения уровня:

цепное :

базисное : (1.16).

Если абсолютное изменение отрицательно, его следует на­зывать абсолютным сокращением. Абсолютное изменение име­ет ту же единицу измерения, что и уровни ряда с добавлением единицы времени, за которую определено изменение: 22 тыс. руб. в год (или в месяц, или в пятилетие). Без указания единицы времени, за которую произошло измерение, абсолютный прирост нельзя правильно интерпретировать.

Таблица 1.4.

Абсолютные и относительные показатели тенденции.

Номер периода	Уровень ряда (тыс. руб.)	Абсолютное изменение уровней (тыс. руб. в год)	Ускорение абсолютного изменения (тыс. руб. в год)	Темп роста уровня к периоду, %
				предыдущему	Начальному
0 (начальный)	100	-	-	-	-
1	112	12	-	112	112
2	128	16	4	114,3	128
3	148	20	4	115,6	148
4	172	24	4	116,2	172
5	200	28	4	116,3	200
6	232	32	4	116.0	232

В табл. 1.4 абсолютное изменение уровня не является кон­стантой тенденции. Оно со временем возрастает, т.е. уровни ряда изменяются с ускорением. Ускорение - это разность меж­ду абсолютным изменением за данный период и абсолютным из­менением за предыдущий период равной длительности:

(1.17).

Показатель абсолютного ускорения применяется только в цепном варианте, но не в базисном. Отрицательная величина ускорения говорит о замедлении роста или об ускорении сниже­ния уровней ряда.

Как видно из табл. 1.4, ускорение является константой тен­денции данного ряда, что свидетельствует о параболической форме этой тенденции. Ее уравнение имеет вид:

(1.18),

где где у₀ - уровень ряда в начальный (нулевой) период; а - средний абсолютный прирост (по всему ряду); b - половина ускорения; - номера периодов.

По данным табл. 1.4 имеем:

Показатель ускорения абсолютного изменения уровней вы­ражается в единицах измерения уровня, деленных на квадрат длины периода. В нашем случае ускорение составило 4 тыс. руб. в год за год. Смысл показателя следующий: стоимость объема продаваемых акций имел абсолютный при­рост, возрастающий на 4 тыс. руб. в год ежегодно.

Усвоить рассмотренные показатели поможет следующая аналогия с механическим движением: уровень - это аналог прой­денного пути, причем начало его отсчета не в нулевой точке; абсолютный прирост - аналог скорости движения тела, а уско­рение абсолютного прироста - аналог ускорения движения. Пройденный телом путь, считая и тот, который уже был прой­ден до начала отсчета времени в данной задаче, равен:

(1.19),

где - путь, пройденный до начала отсчета времени; v – скорость движения; а - ускорение; t - время, прошедшее от начала его отсчета в задаче.

Система показателей должна содержать не только абсолют­ные, но и относительные статистические показатели. Относи­тельные показатели динамики необходимы для сравнения развития разных объектов, особенно если их абсолютные характеристики различны. Предположим, что тенденция объема продаж другого вида ценных бумаг характеризуется следующим уравнением: . И абсолют­ный прирост, и ускорение роста объема продаж во втором случае гораздо меньше, чем в первом. Но можно ли ограничиться этими показателями и сделать вывод, что развитие продаж вто­рого вида ценных бумаг происходит более медленными темпами, чем первого? Меньший уровень еще не есть меньший темп разви­тия, и это покажет относительная характеристика тенденции динамики - темп роста.

Темп роста - это отношение сравниваемого уровня (более позднего) к уровню, принятому за базу сравнения (более ранне­му). Темп роста исчисляется в цепном варианте - к уровню предыдущего года, а в базисном - к одному и тому же, обыч­но начальному уровню. Он свидетельствует о том, сколько процентов составляет срав­ниваемый уровень по отношению к уровню, принятому за базу, или во сколько раз сравниваемый уровень больше у ровня, при­нятого за базу. При этом если уровни снижаются со временем, то сказать, что последующий уровень «больше в 0,75 раза», или составляет 75% базового уровня, это, разумеется, означает, что уровень уменьшился на четверть. Темп изменения в разах всегда говорит о том, во сколько раз сравниваемый уровень больше предыдущего.

Рассмотрим связь абсолютных и относительных показателен динамики. Обозначим темп изменения через k, тогда имеем:

цепной темп роста в период с номером n:

базисный темп роста за весь период:

Если сравниваемый уровень выразить через уровень базис­ного (или предыдущего) периода и абсолютное изменение, по­лучим:

(1.17).

Величина k в уравнении (1.17), т.е. отношение абсолютного изменения к уровню предыдущего (или базисного) года, называется относительным приростом (относительным сокращением, относительным изменением, процентным изменением) или темпом прироста.

Темп изменения - величина всегда положительная. Если уро­вень ряда динамики принимает положительные и отрицатель­ные значения, например, финансовый результат от реализации продукции предприятием может быть прибылью (+), а может быть убытком (-), тогда темп изменения и темп прироста при­менять нельзя. В этом случае такие показатели теряют смысл и не имеют экономической интерпретации. Сохраняют смысл только абсолютные показатели динамики.

Рассмотрим соотношения между цепными и базисными по­казателями на примере данных табл. 1.4:

1. сумма цепных абсолютных изменений равна базисному абсолютному изменению:

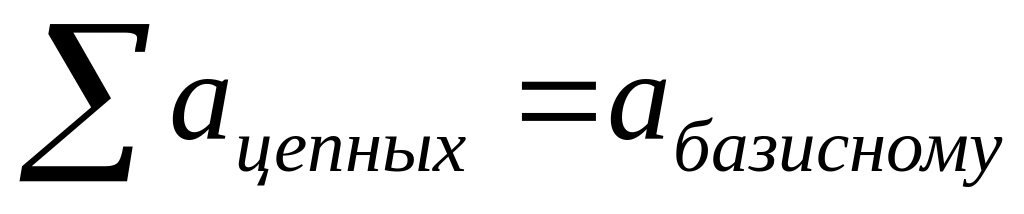
12+16+20+24+28+32=232-100=132

2. произведение цепных темпов изменения равно базисно­му темпу изменения:

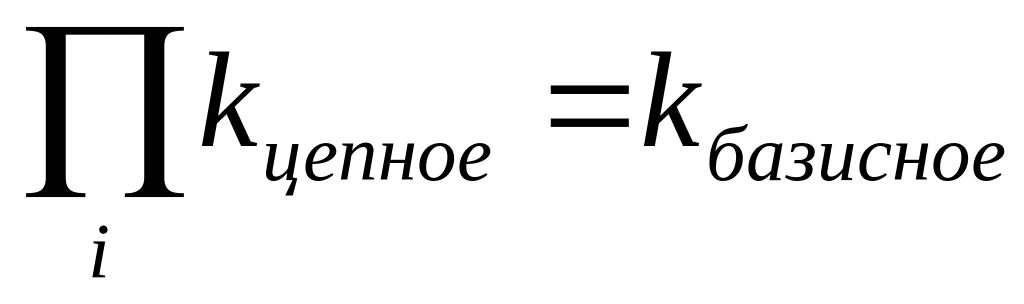
1,12 * 1,143 * 1,156 * 1,162 * 1,163 * 1,16 = 2,32.

Значения цепных темпов прироста, рассчитанных каждый к своей базе, различаются не только числом процентов, но и величиной абсолютного изменения, составляющей каждый про­цент. Следовательно, складывать или вычитать цепные темпы прироста нельзя. Абсолютное значение 1%-ного прироста равно сотой части предыдущего уровня или базисного уровня.

Средний темп изменения определяется наиболее точно при аналитическом выравнивании динамического ряда по экспоненте. Если можно пренебречь колеблемостью, то средний темп определяют как геометрическую среднюю из цепных темпов роста за n лет или из общего (базисного) темпа роста за n лет:

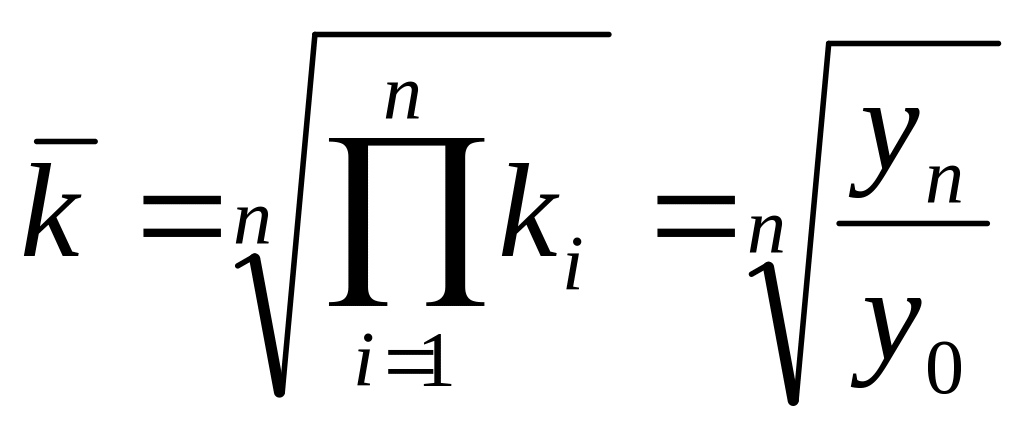(1.5).

Например, стоимость потребительской корзины за год в ре­зультате инфляции возросла в три раза. Каков средний месяч­ный темп инфляции?

, или 1.096%,

т.е. в среднем за месяц цена увеличивалась на 9.6% к уровню пре­дыдущего месяца.

Средний темп роста так же, как средний прирост, следует сопровождать указанием двух единиц времени: периода, который им характеризуется, и периода, на который рассчитан, например, среднегодовой темп за последнее десятилетие; сред­немесячный темп за полугодие и т.д.

Если исходной информацией служат темпы прироста и нуж­но вычислить их среднегодовую величину, то предварительно следует все темпы прироста превратить в темпы роста, приба­вив 1, или 100%, вычислить их среднюю геометрическую и сно­ва вычесть 1, или 100%. Интересно, что ввиду асимметрии темпа прироста и темпа сокращения при равных их величинах общий темп прироста всегда отрицателей. Так, если за первый год объем | производства вырос па 20%, а за второй снизился на 20% (темпы цепные), то за два года имеем:

- средний темп роста или 97,98%;

- средний темп прироста - 1 = -0,0202, или -2,02%.

Интересную задачу представляет определение срока, за кото­рый ряд с большим средним показателем динамики, но меньшим начальным уровнем догонит другой ряд с большим начальным уровнем, по меньшим показателем динамики. Для абсолютных приростов задача элементарна: имеем одни ряд с базисным уров­нем и средним абсолютным приростом ; второй ряд с показателями соответственно , , причем > , < . Уровень первого ряда сравняется с уровнем второго ряда через n лет:

(1.6).