1.4. Дисперсия и среднее квадратическое отклонение.

Если средняя арифметическая выбрана как показатель центра распределения, то соответствующими показателями вариации являются дисперсия и среднее квадратическое отклонение. Дис­персия широко применяется в финансовых расчетах как мера риска и неопределенности. Сред­нее квадратическое отклонение ис­пользуется как мера изменчивости в ценообразовании, например, опционов.

Дисперсия для несгруппированных данных. Если отдельные на­блюдения сгруппированы вблизи среднего значения, то разности между каждым индивидуальным наблюдением , и средней будут небольшими. Если отдельные наблюдения широко рассея­ны, то разности между каждым индивидуальным значением , и средней будут велики.

Можно предположить, что с помощью суммирования всех ( - ) мы получим меру рассеяния. К сожалению, это не так, потому что всегда равна нулю. Для преодоления этого свой­ства средней необходимо возвести в квадрат каждое отклонение ( - ) и просуммировать получившиеся значения. Деление ре­зультата на n-1, т.е. на количество наблюдений минус один, дает дисперсию. Это можно записать в формализованном виде:

(1.5).

Если вычисляется дисперсия на основе всей совокупности данных, то делитель в выражении (1.5) равен n. Однако когда данные, которыми мы располагаем, представляют выборку из всей совокупности данных, что обычно случается в эмпирических ис­следованиях в области финансов, следует делить на n-1. Происходит это потому, что мы должны делить на то, что статистики называют степенями свободы, для предотвращения искажения ре­зультата. Степени свободы - это число наблюдений минус число параметров, оцененных по рассматриваемым данным. В случае дисперсии средняя оценивается по тем же данным. Таким образом, когда эта оценка используется при вычислении среднего квадратического отклонения, число степеней свободы равно n-1. Наибольший эффект при коррекции n на число степеней свободы наблюдается для малых выборок. Понятно, что для большого объ­ема данных эффект коррекции минимален.

Пример. Найдите самостоятельно дисперсию переменной Х, значения которой приведены в таблице 1.3.

Таблица 1.3.

Значения переменной Х

2407,5

2289,2

2160,1

2311,1

2425,8

2378,4

2245,5

2229,2

2118,8

2372,4

2376,3

Ответ: 10520.15.

Дисперсия для сгруппированных данных. При использовании сгруппированных данных формула дисперсии выглядит так:

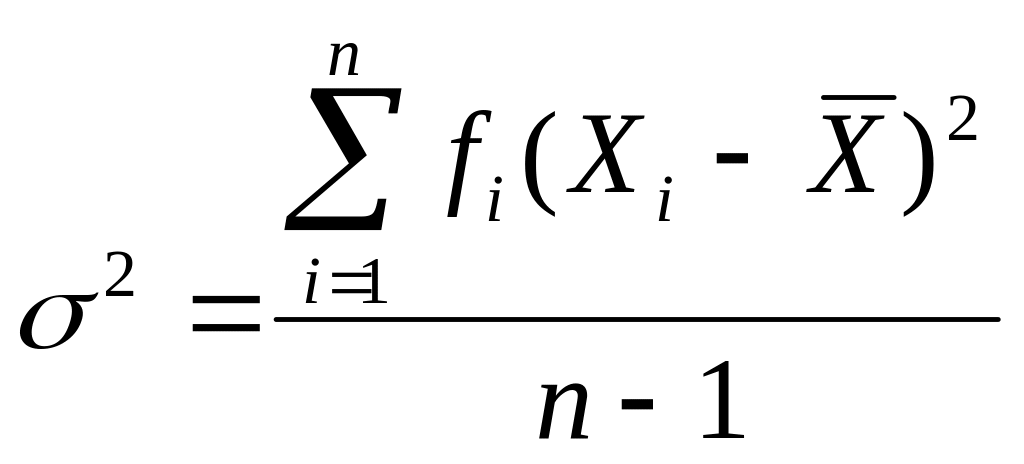(1.6),

где - количество наблюдений в каждом интервале, - центральное значение каждого интервала, а - среднее значение всех Х.

Пример. Вычислить дисперсию сгруппированных данных, представленных в таблице 1.2.

Среднее квадратическое отклонение. Дисперсия выражается в квадратах единиц, находящихся в осно­вании расчета, что делает ее интерпретацию довольно затруднительной. Эту проблему можно преодолеть, извлекая квадратный корень из дисперсии и получая, таким образом, среднее квадра­тическое отклонение, обозначаемое как .

Среднее квадратическое отклонение для несгруппированных данных. Среднее квадратическое отклонение вычисляется так:

(1.7).

Среднее квадратическое отклонение для сгруппированных дан­ных. Формула для нахождения среднего квадратического откло­нения для сгруппированных данных выглядит так;

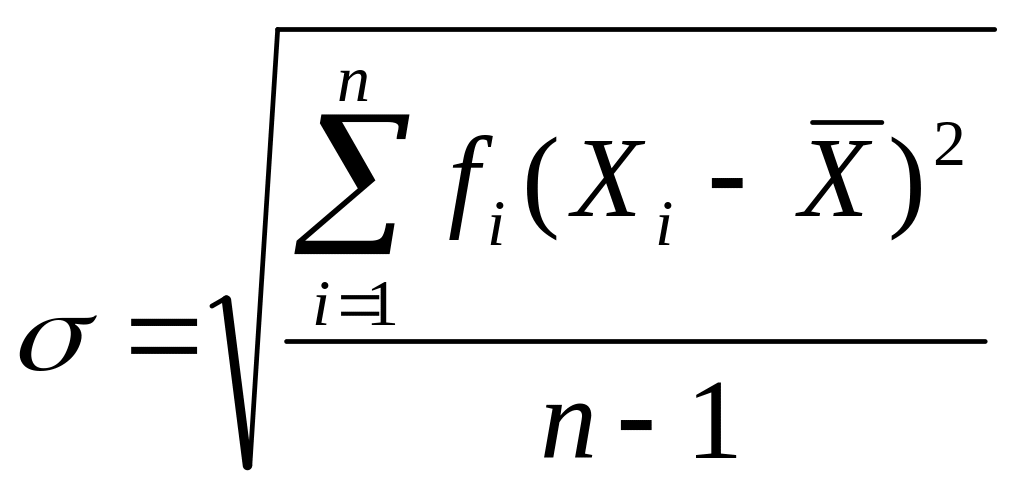(1.8)

Это опять только квадратный корень из диспер­сии, но на этот раз для сгруппированных данных.

Коэффициент вариации. Среднее квадратическое отклонение выражается в единицах из­мерения, лежащих в основе расчета. Таким образом, при срав­нении степени вариации переменных должны быть учтены раз­личия в величине этих переменных. Для этого нужно рассчитать коэффициент вариации. Он находится как отношение:

(1.9).

Коэффициент асимметрии. Иногда бывает важно знать, есть ли смещения в рассеянии данных. Ин­дикатор этих смещений - скошенность (асимметрия) данных. В случае положительной асимметрии распределение имеет длинную правую ветвь. Средняя величина дохода больше медиа­ны, которая в свою очередь больше моды. Значение средней больше медианы и моды, потому что на нее повлияли несколько очень больших значений доходов.

Отрицательная асимметрия проявляется в виде более длинной левой ветви, а величина средней меньше медианы и моды. Боль­шинство наблюдений распределения имеют значения больше средней, но величина средней снижается из-за нескольких очень малых наблюдений.

При симметричном распределении средняя, медиана и мода имеют одно и то же значение.

Показателем асимметрии, который наиболее пригоден для применения в случае сгруппированных данных, является ко­эффициент асимметрии, основанный на расчете моментов рас­пределения. Он определяется с помощью центрального момента третьего порядка и деления его на куб среднего квадратического отклонения, что можно представить следующей формулой:

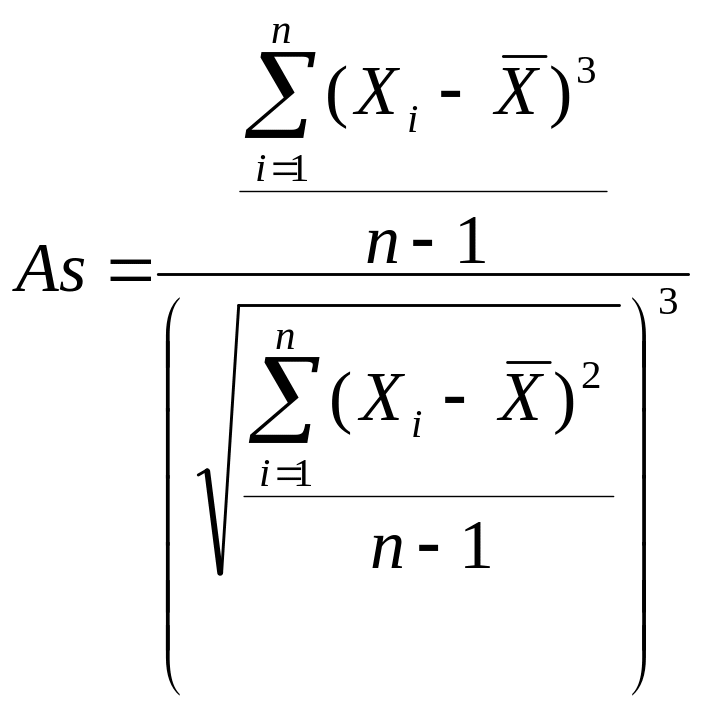(1.10).

Эксцесс. В то время как показатели асимметрии характеризуют симметричность распределения частот, показатели эксцесса описывают пиковость этого распределения. Распределения, имеющие более выраженный пик, чем у нормального распределения (о нем деталь­но рассказано далее), называются островершинными. Те же распре­деления, у которых степень вытянутости вдоль оси ординат меньше, чем у нормальной кривой, называются плосковершинными, а рас­пределения, которые похожи на нормальное, — средневершинными. Островершинные распределения можно увидеть в доходах активов, когда наблюдаются периодические скачки в ценах на эти активы. Рынки с прерывающимся процессом торговли, как, например, рынки ценных бумаг, которые закрываются на ночь и в выходные, имеют большую вероятность для демонстрации скачков цен активов. Причиной служит то, что информация, которая влияет на цены, но публикуется во время закрытия рынков, окажет воздействие на цены, когда рынок откроется вновь, таким образом создавая условия для скачка между преды­дущей ценой закрытия и ценой открытия. Этот скачок цен, наи­более заметный для ежедневных или еженедельных данных, приведет к более высокой частоте повторения больших положи­тельных или отрицательных доходов, чем предполагалось бы, если бы торговля на рынках велась непрерывно. Коэффициенты эксцесса могут быть определены с помощью центральных моментов распределения. Коэффициент эксцесса находится делением центрального момента четвертого порядка на среднее квадратическое отклонение, возведенное в четвертую степень:

(1.11).

Если данные будут нормально распределены, то коэффициент эксцесса, рассчитанный с помощью формулы (1.11), равнялся бы 3.