Интервалы цен некоторой акции.

Интервал	Среднее значение
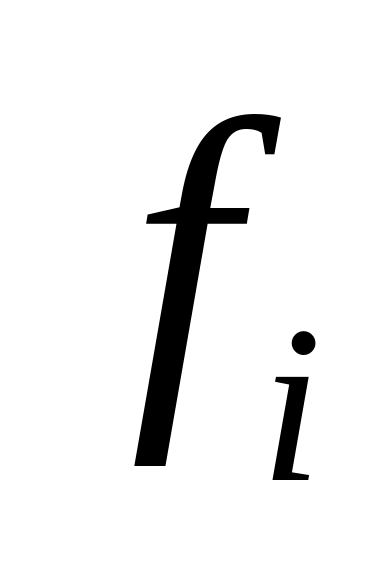
До 260 руб.	215 руб.	20
От 260 до 400 руб.	330 руб.	35
От 400 до 550 руб.	475 руб.	42
Более 550 руб.	585 руб.	15
Итого		112

Средняя арифметическая для сгруппированных данных нахо­дится с помощью следующей формулы

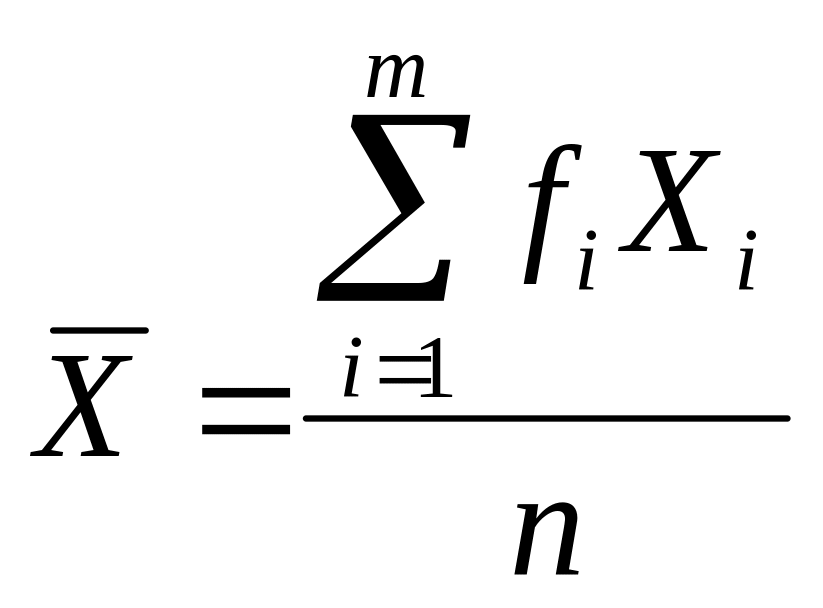(1.3)

где - центральное значение каждого интервала; - количество наблюдений в каждом интервале; т - число интервалов; п - общее количество наблюдений или единиц совокупности.

Используя приведенные выше данные, рассчитаем среднюю арифметическую рыночной цены акции:

руб.

Альтернативным показателем средней арифметической, особен­но хорошо подходящим для измерения средних темпов роста, является средняя геометрическая. Для иллюстрации этого сначала предположим, что фондовый индекс изменялся со следующими годовыми темпами прироста в течение пяти лет: + 10%, + 20%, + 15%, —30%, + 20%. Средняя арифметическая темпов приросту равна + 35/5 = 7. Однако 100 единиц, инвестированных в пер­вый год, возрастут до следующих значений в каждом году соот­ветственно: 110; 132; 151,8; 106,26; 127,51. Следовательно, фак­тический прирост за весь пятилетний период составляет лишь 27,5%. Разделив это число на пять, мы получим 5,5% в год; но правильный ли это ответ?

Правду говоря, нет! Что нам действительно нужно, так это единичная мера темпа прироста, которая при повторении ее n раз трансформирует начальное значение в конечное. Корректный по­казатель периодических темпов прироста находится с использова­нием средней геометрической. Для измерения среднего годового темпа прироста за n лет используется следующая формула:

(1.4)

где имеют вид (1 + r), а величина r, темп прироста, выражена в десятичных дробях, т.е., например, 10% = 0,1.

При использовании приведенных выше данных средняя геомет­рическая из темпов прироста в течение пяти лет составит 4,98%:

Таким образом, средняя арифметическая дает преуве­личенное значение среднего годового темпа прироста в данном примере. Применение же средней геометрической дает коррект­ную "среднюю" темпа прироста.

Какую среднюю использовать? Выбор подходящего вида средней зависит, с одной стороны, от природы данных, а с другой - от того, как этот показатель будут использовать. Средняя арифметическая особо чувствительна к экстремаль­ным (выделяющимся) значениям в одном из направлений, кото­рые называются смещенными данными. Выделяющиеся большие значения увеличивают среднюю выше уровня действительного представляющего точку центра распределения данных. Особо малые значения признаков имеют противоположный эффект. Иногда для того чтобы исключить влияние экстремальных еди­ниц данных, рассчитывается усеченная средняя. Для этого просто необходимо удалить 5% наибольших и 5% наименьших наблю­дений до расчета средней арифметической.

Экстремальные наблюдения не влияют на медиану и моду, но эти показатели не столь полезны в дальнейшем матема­тическом и статистическом анализе.

Средняя геометрическая лучше других подходит, когда под­считываются "средние" темпы прироста в течение нескольких временных периодов.