Показатели центра распределения.

Практически каждый человек знаком с понятием средней величины, будь это "средний" размер остатка по кредитной карте, "среднее" число операций по счету и т.д. Фактически существует несколько показателей "средней", которые особенно интересны в сфере финансов. Это:

• мода;

• медиана;

• средняя арифметическая;

• средняя геометрическая.

Мода - это наиболее часто наблюдаемая величина изучаемой переменной. Для ее иллюстрации рассмотрим следующие дан­ные, которые показывают цену акции, выраженную в рублях, в течение 15-дневного периода:

100, 120, 90, 80, 100, 150, 140, 120, 110, 100, 120, 120, 100, 120, 110.

Модой, т.е. наиболее часто повторяющимся наблюдением, является величина 120.

Медиана - это значение наблюдения, которое находится в сере­дине ранжированного ряда данных, т.е. наблюдение, занимаю­щее срединное положение.

Медиана для несгруппированных данных. Для определения ме­дианы в случае несгруппированных данных мы сначала должны расположить их в возрастающем порядке. Покажем это на при­мере, использованном при рассмотрении моды

80, 90, 100, 100, 100, 100, 110, 110, 120, 120, 120, 120, 120, 140, 150.

Так как присутствуют 15 наблюдений, медианой является значение восьмого наблюдения, т.е. величина признака, равная 11.

Если бы в примере было четное число наблюдений, то отсут­ствовало бы "срединное" наблюдение, поэтому была бы рассчитана средняя из двух значений, стоящих посередине. Ре­зультатом может являться число, не присутствующее на самом деле в ряду данных.

Средняя арифметическая — наиболее часто используемый пока­затель центра распределения, именно ее большинство людей рассматривают в качестве средней.

Средняя арифметическая для несгруппированных данных. Средние показатели динамики - средний уровень ряда, сред­ние абсолютные изменения и ускорения, средние темпы роста - характеризуют тенденцию. Они необходимы при обобщении характеристик тенденции за длительный период, по различным периодам; они незаменимы при сравнении развития за неодинаковые по длительности отрезки времени и при выборе ана­литического выражения тренда. При наличии в динамическом ряду существенных колебании уровней определение средних по­казателей тенденции требует применения специальных методов статистики. В дан­ном разделе рассматриваются только математические свойства средних показателей динамики и простейшие приемы их вычисления, применимые па практике к рядам со слабой ко­леблемостью.

Средняя арифметическая рассчитывается суммированием всех значений отдельных наблюдений и последующим делением по­лученной суммы на количество наблюдений. Например, допус­тим, что мы желаем подсчитать среднюю арифметическую цены какого-либо актива в течение пяти дней. В данный период мы наблюдаем следующие цены

225 225 240 215 230

Найдем среднюю арифметическую, складывая эти пять значений и деля сумму на число наблюдений. В формализован­ном виде средняя арифметическая выглядит так:

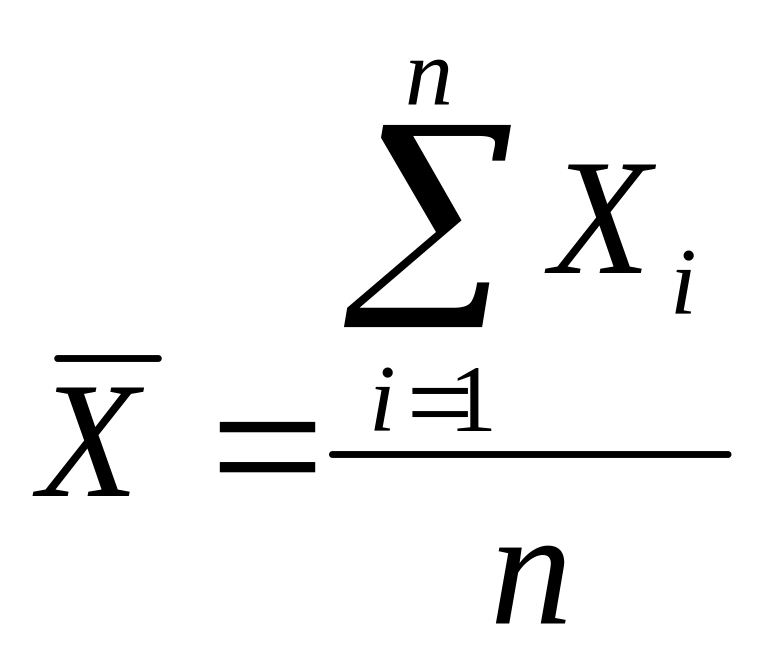(1.2).

Здесь показано, что - это сумма (отдельных наблюдений X), поделенная на количество наблюдений. Греческая заглавная буква сигма ( ) - оператор суммирования, означает, что все необходи­мо сложить вместе. Так как в нашем примере всего пять , то опе­ратор суммирования будет выглядеть следующим образом , показывая, что первые пять должны быть сложены друг с другом. Сейчас мы можем подсчитать среднюю арифметическую пя­ти цен ценной бумаги: (225 + 225 + 240 + 215 + 230)/5 = 227.

Таким образом, средняя арифметическая цена равняется 227.

В моментном ряду смысл среднего уровня заключается в том, что он характеризует уже не состояние объекта в отдельные моменты, а его среднее, обобщенное состояние между на­чальным и конечным моментами учета. Из этого следует, что уровни, относящиеся к начальному и конечному моментам, иг­рают не ту роль, что уровни, относящиеся к моментам внутри изучаемого отрезка времени. Начальный и конечный уровни находятся на границе изучаемого интервала, они наполовину относятся к предыдущему и последующему интервалам и лишь наполовину к изучаемому. Уровни, относящиеся к моментам внутри осредняемого интервала, целиком относятся только к нему. Отсюда получаем особую форму средней арифметичес­кой величины, называемой хронологической средней:

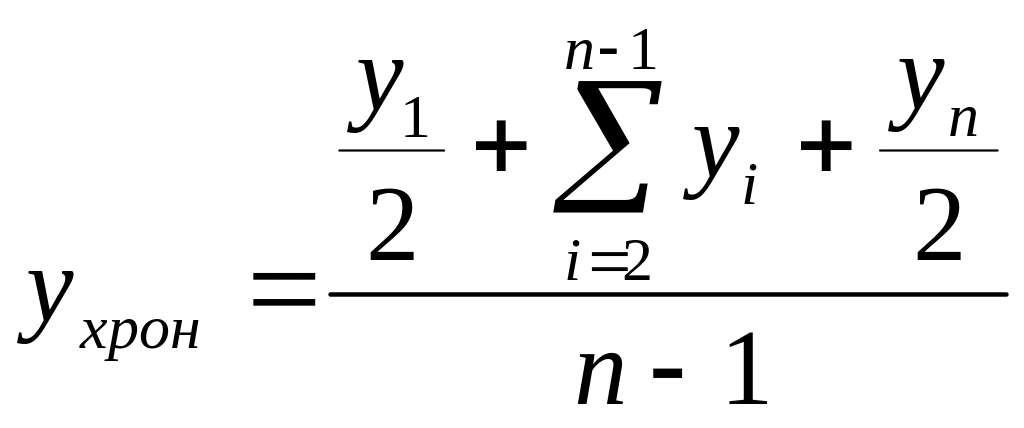(1.3).

Проблема вычисления среднего уровня моментного ряда при неравных промежутках между моментами является спорной и здесь не рассматривается. Если известны точные даты изменения уровней моментного ряда, то средний уровень определяется как

(1.4).

Средний абсолютный прирост (абсолютное изменение) определяется как простая арифметическая средняя из абсолютных изменений за равные промежутки времени (цепных абсолютных изменений) или как частное от деления базисного абсолютного изменения на число осредняемых отрезков времени от базисно­го до сравниваемого периода:

(1.5).

Средняя арифметическая для сгруппированных данных. Часто верхние и нижние пределы крайних интервалов остаются откры­тыми. Следовательно, необходимо сделать допущение о границах интервалов. Это допущение должно базироваться на характери­стиках анализируемых данных. Например, данные из табл. 1.2. относятся к рыночной цене акции, которую наблюдали некоторое время аналитики. Нижний интервал обозначен "До 260 руб.", а верхний — "Более 550 руб.".

Таблица 1.2.