Пример. На множестве вещественных чисел R задано отношение f = {(х, у): y x2 , где х, у R} – функция. Но обратное отношение f 1 = {(х, у): x y2 , где х, у R} уже функцией не является, ему например, принадлежат пары (4, 2) и (4, –2).

Чтобы условие однозначности выполнялось для отношения f 1 , функ-

ция f должна быть, очевидно, инъективной.

Так как всякая функция – это бинарное отношение, композиция функций строится, как композиция бинарных отношений.

Пусть z = f (х) и у = g (z). Их композиция ( f g) определяется обычным образом: ( f g) = g (f (х)).

Композиция взаимно однозначных функций – взаимно однозначная функция, при этом f g 1 g 1 f 1 .

Пример. Пусть f (х) = 2х + 1, g(х) = 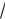х , тогда

( f g)( x) (g f )( x) .

1.5. Отношение эквивалентности

Определениие. Бинарное отношение, обладающее свойствами рефлексивности, симметричности и транзитивности, называется отношением эквивалентности.

Если на множестве А задано отношение R, то это множество А разбивается на классы эквивалентных между собой элементов, которые называются классами эквивалентности. Действительно, в силу свойства транзитивности любые два класса эквивалентности либо совпадают, либо не пересекаются. Каждый класс эквивалентности можно рассматривать как один элемент нового множества – множества классов эквивалентности. Это множество классов эквивалентности называется фактор-множеством множества А по отношению эквивалентности R и обозначается A/R. Так как классы смежности не пересекаются, то каждый из этих классов однозначно определяется указанием любого его (элемента («представителя класса»).

Примеры. 1. Отношение сравнимости по модулю m, заданное на множестве целых чисел, является отношением эквивалентности. Фактор-мно- жество по этому отношению называется группой вычетов множества целых чисел по модулю т и обозначается Z/тZ или Zm (под mZ понимается множество всех целых чисел, делящихся на т: mZ = m{…, –3, –2, –1, 0 1, 2, 3, …} = {…, –3m, –2m, –m, 0, m, 2m 3m, …}). Каждый класс смежности –

14

это множество целых чисел, которые дают одинаковый остаток от деления на т, его можно задать любым его представителем, например, можно писать Zm={0, 1, 2, …, m – 1}, но под каждым из этих чисел понимать не только его, но и весь класс смежности, к которому оно принадлежит. В частности, Z/2Z = Z2={0, 1} – это фактор-множество множества всех целых чисел по подмножеству четных чисел, 0 означает множество всех четных чисел (один класс смежности), 1 – множество нечетных чисел (второй класс смежности).

2.Отношение «иметь тот же возраст», заданное на множестве всех людей, есть отношение эквивалентности. «Эквивалентные» люди принадлежат к одной и той же возрастной группе. Фактор-множество – номера годов.

3.В множестве всех студентов страны можно рассмотреть отношение принадлежности одному учебному заведению. Тогда эквивалентны студенты одного учебного заведения, а фактор-множество – множество этих учебных заведений. Среди студентов одного вуза можно рассматривать отношения принадлежности одному факультету или принадлежности одному курсу, или обучения в одной группе. В этих случаях классы эквивалентности – это студенты одного факультета, или одного курса, или одной группы, а фактор-множества – множество факультетов, или множество курсов, или множество групп этого вуза (каждую группу можно упомянуть, указав, например, ее старосту).

4.В множестве дней одного года можно рассмотреть отношение принадлежности одному месяцу или отношение принадлежности одному дню недели. Тогда классы эквивалентности – это дни одного и того же месяца или дни, приходящиеся на один день недели, а фактор-множества – это 12 месяцев или 7 дней недели. т. е. множество из семи элементов: понедельника, вторника, …, воскресенья.

Отношение эквивалентности можно интерпретировать как отношение достижимости на неориентированном графе. Тогда классам эквивалентности будут соответствовать компоненты связности графа: любые вершины из разных компонент связности не достижимы друг из друга, а вершины одной компоненты связности достижимы (граф из примера). Фактор-мно- жеством является множество компонент связности.

Напомним, что отображением множества А в множество В называется сопоставление каждому элементу х множества А некоторого элемента у из множества В, т. е. функция φ: A→B, сопоставляющая каждому элементу

xA некоторый элемент y B : у = φ(х); при этом у называется образом

элемента х, а х – прообразом элемента у. Отображение φ называется моно-

морфизмом, или инъекцией, или отображением «в», если у каждого эле-

мента y B имеется не более одного прообраза (т. е. если у y B есть прообраз, то только один); оно называется эпиморфизмом, или проекцией, или

15

отображением «на», если у каждого элемента y B имеется хотя бы один прообраз; оно называется изоморфизмом, или биекцией, или взаимно однозначным соответствием (кратко: 1-1 – соответствием), если оно являет-

ся одновременно и проекцией и инъекцией. Иными словами, 1-1 – соответствие – это отображение, при котором у каждого y B имеется прообраз, причем только один (таким образом, у 1-1–соответствия φ существует и обратное 1-1 – соответствие, обозначаемое φ–1: В→А, которое каждому элементу у из В сопоставляет его прообраз при отображении φ: φ–1(у) = х). Два множества А и В называются эквивалентными, или равномощными (что записывается символом А ~ В), если между ними можно установить взаимно однозначное соответствие (грубо говоря, равномощные множества – это такие, у которых одинаковое число элементов; это понятие позволяет сравнивать даже бесконечные множества). Говорят, что множество А имеет меньшую мощность, чем множество В, а множество В – большую мощность, чем множество А, если не существует биекции (т. е. 1-1 – соответствия) между А и В, но существует биекция между А и некоторым собственным подмножеством множества В. Мощностью множества называется символ, который сопоставляется всем множествам одинаковой мощности. Обозначение мощности множества А: | А| или A («двойное абстрагирование») или какой-нибудь греческой буквой, напимер |A| = A = α. В частности, мощностью конечного множества считается число его элементов. Например, если А – множество клеток шахматной доски, то A = 64, а если А – множество дней недели, то A = 7. Справедлива теорема Ф. Бернштейна «о трихотомии»: для любых двух множеств с мощностями

αи β соответственно обязательно выполняется одно из 3 соотношений: α = β,

α< β, α > β (т. е. любые 2 множества сравнимы по количеству их элементов). Очевидно, что отношение эквивалентности множеств обладает всеми свойствами понятия эквивалентности: 1) A ~ A; 2) если A ~ B, то B ~ A; 3) если A ~ B и B ~ C, то A ~ C.

Множества, равномощные с натуральным рядом, т. е. с множеством N = {1, 2, 3, …, n, …} называются счетными; их мощность обычно обозна-

чается символом п = N . Иными словами, счетные множества – это те множества, элементы которых можно расположить в одной последовательности х1, х2, …, хn, … (индекс и есть то натуральное число, которое сопоставляется элементу счетного множества). Например, множество всех четных чисел счетно; соответствующая биекция φ(k) = 2k, или хk = 2k. Интересно, что множество Q всех рациональных чисел тоже счетно (напоминаем, что рациональным числом называется любая дробь, т. е. отношение 2 целых чи-

сел r qp ). Иными словами, справедлива теорема: Q = п.

16

Доказательство. Запишем сначала все дроби, у которых сумма числителя и знаменателя равна 2 (такое число одно: r1 11 ), затем те, у которых

сумма числителя и знаменателя равна 3 (т. е. r2 12 , r3 12 ), затем те, у ко-

сти, мы в группе чисел с номером п запишем п дробей, у которых сумма числителя и знаменателя равна п + 1. В этой последовательности, очевидно, появятся все положительные дроби (так как у каждой дроби есть некоторая сумма числителя и знаменателя), но каждая дробь появится бесконечно много раз. Однако мы можем удалить из получившейся последовательности все сократимые дроби, и тогда получим последовательность tn всех положительных рациональных чисел, в которой каждое число встречается только один раз. Чтобы расположить в одну последовательность все рациональные числа – положительные, отрицательные и 0, составим из последовательности tn новую последовательность sn по прави-

лу: s1 = 0, s2k = tk, s2k+1 = – tk, k = 1, 2, 3, … . В последовательности sn расположены все рациональные числа, причем каждое – по одному разу, а это

означает, что их множество счетно, и теорема доказана.

Определение. Мощность множества всех точек отрезка [0, 1] называется мощностью континуума и обозначается символом с: [0, 1] c .

Теорема. п < c, т. е. множество точек отрезка [0, 1] несчетно, но имеет счетное подмножество (таким образом, точек на отрезке принципиально больше, чем натуральных чисел).

Доказательство. Подмножество точек аn = 1n отрезка [0, 1] счетно.

Осталось доказать, что не существует биекции этого отрезка на счетное множество. Предположим противное, т. е. что такая биекция φ отрезка [0, 1] существует, т. е. что все точки отрезка можно расположить в одну последовательность хn. Каждое число отрезка [0, 1] можно записать в виде бесконечной десятичной дроби, причем однозначно, если исключить записи, в которых после некоторой цифры все последующие цифры равны 9. Обозначим последовательные десятичные цифры числа хn через хnk, т. е.

φ(п) = хn = 0, хn1хn2хn3…хnk…, где хnk означает k-ю цифру числа хn. Составим бесконечное десятичное число у, каждая цифра которого отличается

на 1 от соответствующего десятичного знака числа хn, т. е. число у = 0, (х11 ± 1) (х22 ± 1)(х33 ± 1) …(хnn ± 1)… (знак «+» или «–» перед единицей

17

можно выбирать произвольно, если только соответствующая цифра хпп не является нулем или девяткой). Это число у принадлежит отрезку [0, 1] и поэтому должно совпадать с одним из чисел х1, х2, х3,…, хn…, например у = хm. Но оно не может совпадать с хm, так как десятичная цифра с номером т у чисел у и хm – разная (они отличаются на единицу по построению). Полученное противоречие доказывает, что предположение неверно, и теорема доказана.

Следствия. 1. Все отрезки имеют мощность континуума. Действительно, биекция между [0, 1] и [a, b] задается формулой у = a + (b – a)x. 2. Любой интервал имеет мощность котинуума. Для доказательства доста-

точно установить биекцию φ между [0, 1] и (0, 1). Построим ее так: φ(0) = 12 ,

у = φ(х) (0, 1). 3. Множество точек любой окружности имеет мощность континуума: очевидна биекция между окружностью и полуоткрытым интервалом [0, 2πR), а по предыдущему существует биекция между [0, 2πR) и [0, 1]. 4. Множество точек любой прямой имеет мощность континуума. Со-

М(х, у) квадрата D = [0, 1] × [0, 1], т. е. точек, у которых 0 ≤ х ≤ 1, 0 ≤ у ≤ 1 тоже имеет мощность континуума, т. е. справедлива следующая теорема:

[0, 1] [0, 1] = с.

Доказательство. Как и ранее, каждую точку t отрезка [0, 1] запишем в виде бесконечной десятичной дроби: t = 0,t1t2t3…. Соответствующая би-

екция φ(t) = (x, y) задается формулами: х = 0,t1t3t5t7…, у = 0,t2t4t6t8… (например, точке t = 0,314159265358… отрезка [0, 1] биекция сопоставляет

точку М(х, у) квадрата, координаты которой таковы: х = 0,345255…, у = 0,119638…) и эта биекция доказывает теорему.

Замечание. Аналогично доказывается, что и трехмерный, и четырехмерный куб, и куб любой конечной размерности имеет мощность континуума. Отсюда следует, что множество всех точек плоскости R2, трехмерного пространства R3 и любого конечномерного пространства Rn имеет мощность континуума. Может показаться, что множеств с большей мощностью, чем мощность континуума, не существует. Но это не так. Рассмотрим множество всех подмножеств данного множества А мощности α. Его мощность обозначается символом 2α. Это обозначение связано с тем, что если множество конечно и содержит п элементов, то число всех его подмножеств (включая несобственные) равно 2n (действительно, если обозна-

18

чить элементы данного множества через х1, х2, х3,…, хn, то каждому подмножеству этого множества взаимно однозначно соответствует упорядоченный набор из п нулей и единиц, в котором единицы соответствуют элементам, вошедшим в подмножество, а нули – тем, которые не вошли. Например подмножеству из трех элементов А = {x2, х4, х5} соответствует набор {0101100…0}. Таких наборов из п нулей и единиц, очевидно, насчитывается 2n). Для наглядности перечислим все 23 = 8 подмножеств множества А = {x1, х2, х3}, состоящего из трех элементов: {Ø}, {x1}, {x2}, {x3}, {x1, х2}, {x1, х3}, {x2, х3}, {x1, х2, х3}.

Теорема. Каково бы ни было множество А мощности α, существует множество большей мощности, например, 2α > α.

Доказательство. То, что данное множество эквивалентно некоторому набору своих подмножеств, очевидно: оно эквивалентно набору одноэлементных подмножеств. Поэтому надо доказать, что не существует биекции между данным множеством и множеством всех его подмножеств. Предположим противное, т. е. что существует биекция φ, сопоставляющая каждому элементу х данного множества некоторое его подмножество В = φ(х). Возможны два варианта: 1) элемент х входит в множество В, которое ему сопоставляет биекция φ, такие элементы будем называть «хорошими»; 2) элемент х не входит в множество В, которое ему сопоставляет биекция φ, такие элементы будем называть «плохими». Рассмотрим подмножество С всех «плохих» элементов. Этому подмножеству биекция φ сопоставляет некоторый элемент х0 = φ(С) данного множества. Он не может быть «хорошим», так как входит в подмножество всех «плохих» элементов, и значит, он сам – «плохой». Но он не может быть и «плохим», так как иначе (т. е. если бы он был «плохим») он входил бы в то множество С «плохих» элементов, которое ему сопоставляет биекция φ, и, следовательно, был бы «хорошим». Итак, элемент х0 – не является ни «хорошим», ни «плохим». Но каждый элемент обязательно либо «хороший», либо «плохой». Получили противоречие. Значит, предположение неверно, и теорема доказана.

Утверждение 1. Мощность бесконечного множества не изменится, если к нему присоединить любое счетное множество (т. е. объединить со счетным множеством).

Доказательство. Объединим данное бесконечное множество М со счетным множеством Х = {х1, х2, …, хп,…}. Полученное множество обозначим через А = М Х. Требуется установить биекцию между А и М. Для этого выберем в М какое-нибудь счетное подмножество Y = {y1, y2, …, yп,…}. Тогда объединение Z = X Y = {z1, z2, …, zп,…} тоже счетно (соответствующая

19

биекция φ: z2k–1 = xk, z2k = yk, k = 1, 2, 3,…). Все элементы М и А = М Х, не входящие в Х и Y, одинаковы, поэтому биекция φ сопоставит каждый из этих

элементов самому себе. Построенная биекция доказывает утверждение.

Утверждение 2 (признак бесконечности множества). Множество бесконечно тогда и только тогда, когда оно эквивалентно некоторому своему собственному подмножеству.

Доказательство. Множество А бесконечно тогда и только тогда, когда из него можно выделить собственное счетное подмножество Х. По предыдущему утверждению множества А и М = А\Х эквивалентны, что и требовалось доказать.

Произведением двух мощностей α и β называется мощность прямого произведения двух множеств А и В, мощность одного из которых равна α, а другого β (очевидно, что произведение мощностей не зависит от выбора множеств А и В, а зависит только от их мощностей). Аналогично определяется α1 α2 α3…αn – произведение любого числа мощностей, αk = αα…α – произведение k множителей.

Ясно, что мощность прямого произведения конечных множеств равна произведению чисел элементов множеств А и В. Если A = m, B = n, то A B = m n. Выше мы доказали, что kn = n, n2 = n,…, nk = n, kc = c, c2 = c,

…, ck = c, 2c >c и т. д.

20