
- •1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
- •1.1. Основные понятия и определения
- •1.2. Определение и свойства бинарных отношений
- •1.3. Способы задания бинарных отношений
- •1.4. Функции
- •1.5. Отношение эквивалентности
- •2. ЛОГИЧЕСКИЕ (БУЛЕВЫ) ФУНКЦИИ
- •2.1. Обзор логических функций
- •2.2. Свойства конъюнкции, дизъюнкции и отрицания
- •2.3. ДНФ, СДНФ, КНФ, СКНФ
- •2.6. Полиномы Жегалкина
- •2.7. Суперпозиция функций. Замыкание набора функций. Замкнутые классы функций. Полные наборы. Базисы
- •2.8. Некоторые приложения теории булевых функций
- •2.8.1. Функциональные элементы и схемы
- •3. ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
- •3.1. Общие понятия теории графов
- •3.2. Эйлеровы и полуэйлеровы графы
- •3.3. Деревья и их простейшие свойства
- •3.5. Cети и потоки в сетях. Теорема Форда – Фалкерсона
- •3.6. Раскраска графа
- •4.1. Решение типовых примеров
- •4.2. Индивидуальные задания
- •4.3. Дополнительные задачи
- •4.4. Вопросы для самопроверки
- •Список литературы
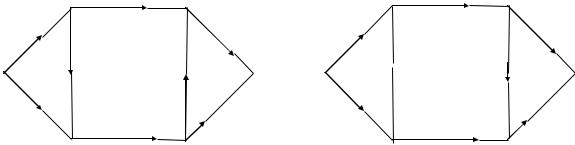
как 20 меньше 25, то мы получаем указанную пометку. Теперь можно пометить вершину 3 пометкой (+2, 15) и вершину 5, пометка которой будет (–3, 25). Только после этого мы можем пометить вершину 6 (сток),
пометка которой будет (+5, 20). δ = min{∞, 25, 20, 15, 25, 20}= 15. Таким образом, наш поток можно увеличить на 15 единиц, прибавляя эти 15 единиц вдоль рассматриваемого пути к прямым дугам и вычитая из обратных с учетом возможного «разворота» обратных дуг. Результат всех этих действий изображен на рис. 4.3.
Таким образом мы получили новый поток, изображенный на рис. 4.4.
|
2(–4,20) |
3(+2,15) |
|
2(+4,5) |
20 |
3 |
|
|
|
|
|||
|
5 + 15 |
|
10 |
|
|
|
10 |
|
10 |
|
|
10 |
|
|
|
|
|
|||
1(∞) |
5–15 |
5–15 6(+5,15) |
|
10 |
|
10 6 |
1 |
|
|
||||
|
|
5 + 15 |
|
|
|
|
5 + 15 |
|
|
|
|
20 |
|
|
|
20 |
|
|
||
|
|
|
|
|
||
|
4(+1,25) 10 |
5(–3,15) |
|
4(+1,10) |
10 |
5 |
|
Рис. 4.3 |
|
Рис. 4.4 |
|
||
После этого для нового потока, изображенного на рис. 4.4, снова расставляем пометки, которые также изображены на рис. 4.4. Мы видим, что для этого потока (кроме источника) можно пометить только 2 вершины, а именно, вершину 4 (ее пометка будет (+1, 10)) и (после этого) вершину 2, пометка которой будет (+4, 5). Больше ничего пометить нельзя, так как из множества помеченных вершин (Y) в множество непомеченных вершин (Z) идут только прямые, насыщенные дуги (дуги (2–3) и (4–5)). Эти две дуги образуют минимальное сечение, величина которого равна 30 условных единиц, и эта же величина равна величине потока (заметим, что величина потока также равна «количеству груза», вывозимого из источника и равна количеству груза, ввозимого в сток). Таким образом, поток на рис. 4.4 является максимальным, а дуги (2–3) и (4–5) образуют минимальное сечение, которому равен наш поток.
4.2.Индивидуальные задания
Взадании 1 требуется привести данные выражения к ДНФ, пользуясь правилами де Моргана. Если возможно, сократить ДНФ, используя свойство поглощения и правило Блейка.
|
|
|
|
|
1. а) x ( y z x z ) ; |
б) |
x y z x y z x y x y x y z . |
||
|
|
|
б) |
x y z x y z x z x y z . |
2. а) x y (x y z x y) ; |
||||
79

|
|
|
|
|
|
|
|
|
|
б) |
x y z x y z x y z x y z x y z . |
3. а) x1 x2 x3 (x1 x3 x4 ) ; |
|||||||||||
|
|
|
|
б) |
x y z x yz x z x y z . |
||||||
|
|
|
|
|
|
|
|
|
|
||
4. а) x z (x y z x y) ; |
|||||||||||
5.а) (x y z y z) (x y y z) ; б) x y z x y z x y z x y z x y z .
6.а) (x y z y z) (x y y z) ; б) x y z x y z x y z x y x z .
7.а) x y (x y z x y) ;
8.а) x y (x y z) x z ;
9.а) x y (x y z x y) ;
10.а) x y z y x z ;
11.а) z( yx xz) ;
12.а) x y(x yz x y) ;
13.а) x1 x2 x3 (x1 x3 x4 ) ;
14.а) xz(x yz xy) ;
15.а) (x yz yz) (x y yz) ;
16.а) (x yz yz) (x y yz) ;
17.а) x y(x yz x y) ;
18.а) x y (x yz) x z ;
19.а) x y ( yz x y) ;
20.а) x yz yxz ;
б) x y z x y z x y z x y z x y z .
б) x y z x y z x y z x y z x y z .
б) x y z x y z x y z x y z x y .
б) x y x y z x z x y .
б) x yz x yz x y x y x y z .
б) x y z x yz x z x y z .
б) x y z x yz x yz x y z x y z .
б) x yz x yz x y z x y z x y z .
б) x y z x y z x yz x yz x y z .
б) x yz x y z x yz x y x z .
б) x y z x yz x y z x yz x yz .
б) x y z x yz x y z x yz x yz .
б) x yz x y z x yz x yz x y . б) x y x yz xz x y .
В задании 2 требуется: в задаче а) написать по данной ДНФ полином Жегалкина, затем от ДНФ перейти к КНФ, а затем перейти к СКНФ; в задаче б) перейти от данной КНФ к ДНФ, а затем перейти к СДНФ.
1. а) x y y z x ; |
б) (x y z )(x z ) . |
2. а) x y x y z ; |
б) (x y z )( y z) . |
3. а) x y x z z ; |
б) (x z )( y z) . |
4. а) x y z x z x y ; |
б) (x y z )(x y) . |
5. а) x z x y y z ; |
б) (x y z )(x z) . |
6. а) x z x y z ; |
б) (x y)( y z ) . |
7. а) x y x z y z ; |
б) (x y z)(x y z ) . |
8. а) x y y z x z ; |
б) (x y z)(x y) . |
80

9. а) x y y z x z ; |
б) (x y z)( y z ) . |
||
10. |
а) x y x y z ; |
б) (x y z )(x z ) . |
|
11. |
а) x y yz x ; |
б) (x y z)(x z) . |
|
12. |
а) x y x y z ; |
б) (x y z)(y z) . |
|
13. |
а) x y xz z ; |
б) (x z)(y z) . |
|
14. |
а) |
x yz x z x y ; |
б) (x y z)(x y) . |
15. |
а) |
xz x y yz ; |
б) (x y z)(x z) . |
16. |
а) |
x z x yz ; |
б) (x y)(y z) . |
17. |
а) x y xz yz ; |
б) (x y z)(x y z) . |
|
18. |
а) x y yz x z ; |
б) (x y z)(x y) . |
|
19. |
а) x y yz x z ; |
б) (x y z)(y z) . |
|
20. |
а) |
x y x z y ; |
б) (x y z)(x z) . |
В задании 3 требуется:
а) составить таблицу истинности данной функции; б) написать для нее СДНФ и СКНФ (если это возможно);
в) найти по таблице истинности полином Жегалкина для данной функции; г) составить карту Карно для данной функции и найти сокращенную ДНФ.
1. (x y)|(x y z). |
|
2. ((x y) z ((x z) + y). |
|||||||
3. ((x z) + y)) (x| y z). |
4. (x y ) z) (x+ y). |
|
|||||||
5. x (z (y + x z )) . |
|
6. (x y) z ((x y)|z) . |
|
||||||
7. x (z (y + x z)). |
|
8. ((x y) | z) ( x y). |
|
||||||
9. (x z y) | (x y + x z). |
10. (x + (y z) | (x y). |
|
|||||||
11. (x y) ((x y) y z). |
12. ((x y)z ((x | z) + y). |
||||||||
13. (( x z) z) + y)) (x| y z). |
14. (x|z) ~ ((x y ) z) (x+ y). |
||||||||
15. ( x (z |xy) (y+ x z )) . |
16. (x y)z ((x y) | z) . |
||||||||
17. |
x (z y z(y + x z)). |
18. ((x y) | z) ~ ( x y). |
|||||||
19. ((x+ z) y) | ((x|y) + x z). |
20. (x + (y~ z)) (x| y). |
||||||||
В задании 4 с помощью карт Карно по данной таблице истинности |
|||||||||
для функции 4 переменных найти ее сокращенную ДНФ. |
|
||||||||
1. |
|
|
|
|
2. |
|
|
|
|
x3, x4 |
|
|
|
|
|
x3, x4 |
|
|
|
х1, х2 |
0 0 0 1 1 1 1 0 |
x1, x2 |
0 0 0 1 1 1 1 0 |
||||||
0 0 |
1 |
0 |
0 |
1 |
0 0 |
1 |
0 |
0 |
1 |
0 1 |
1 |
0 |
1 |
1 |
0 1 |
1 |
0 |
0 |
1 |
1 1 |
1 |
1 |
0 |
1 |
1 1 |
0 |
1 |
1 |
0 |
1 0 |
1 |
1 |
1 |
1 |
1 0 |
0 |
0 |
0 |
1 |
81
3. |
|
|
|
|
|
4. |
|
|
|
|
x3, x4 |
|
|
|
|
|
x3, x4 |
|
|
|
|
x1, x2 |
0 0 0 1 1 1 1 0 |
|
x1, x2 |
0 0 0 1 1 1 1 0 |
||||||
0 0 |
1 |
1 |
0 |
0 |
|
0 0 |
1 |
0 |
0 |
1 |
0 1 |
1 |
1 |
0 |
0 |
|
0 1 |
1 |
0 |
0 |
1 |
1 1 |
1 |
1 |
0 |
0 |
|
1 1 |
0 |
1 |
1 |
0 |
1 0 |
1 |
0 |
0 |
1 |
|
1 0 |
0 |
1 |
1 |
1 |
5. |
|
|
|
|
|
6. |
|
|
|
|
x3, x4 |
|
|
|
|
|
x3, x4 |
|
|
|
|
x1, x2 |
0 0 0 1 1 1 1 0 |
x1, x2 |
0 0 0 1 1 1 1 0 |
|||||||
0 0 |
0 |
|
0 |
1 |
0 |
0 0 |
0 |
1 |
1 |
1 |
0 1 |
1 |
|
0 |
0 |
1 |
0 1 |
1 |
1 |
0 |
1 |
1 1 |
0 |
|
0 |
1 |
0 |
1 1 |
1 |
1 |
0 |
0 |
1 0 |
1 |
|
0 |
0 |
1 |
1 0 |
0 |
0 |
1 |
0 |
7. |
|
|
|
|
|
8. |
|
|
|
|
x3, x4 |
|
|
|
|
|
x3, x4 |
|
|
|
|
x1, x2 |
0 0 0 1 1 1 1 0 |
|
x1, x2 |
0 0 0 1 1 1 1 0 |
||||||
0 0 |
0 |
1 |
1 |
0 |
|
0 0 |
1 |
1 |
1 |
0 |
0 1 |
0 |
0 |
1 |
1 |
|
0 1 |
1 |
1 |
0 |
0 |
1 1 |
0 |
0 |
0 |
1 |
|
1 1 |
1 |
1 |
1 |
1 |
1 0 |
1 |
0 |
0 |
0 |
|
1 0 |
1 |
1 |
1 |
0 |
9. |
|
|
|
|
|
10. |
|
|
|
|
x3, x4 |
|
|
|
|
|
x3, x4 |
|
|
|
|
x1, x2 |
0 0 0 1 1 1 1 0 |
|
x1, x2 |
0 0 0 1 1 1 1 0 |
||||||
0 0 |
1 |
0 |
0 |
0 |
|
0 0 |
1 |
1 |
1 |
1 |
0 1 |
1 |
0 |
1 |
1 |
|
0 1 |
0 |
1 |
1 |
0 |
1 1 |
1 |
0 |
1 |
1 |
|
1 1 |
0 |
0 |
0 |
0 |
1 0 |
0 |
1 |
1 |
0 |
|
1 0 |
1 |
0 |
1 |
1 |
11. |
|
|
|
|
|
12. |
|
|
|
|
x3, x4 |
|
|
|
|
|
x3, x4 |
|
|
|
|
х1, х2 |
0 0 0 1 1 1 1 0 |
|
x1, x2 |
0 0 0 1 1 1 1 0 |
||||||
0 0 |
1 |
0 |
0 |
1 |
|
0 0 |
0 |
1 |
1 |
0 |
0 1 |
1 |
0 |
0 |
1 |
|
0 1 |
0 |
1 |
1 |
0 |
1 1 |
1 |
0 |
0 |
1 |
|
1 1 |
0 |
0 |
0 |
0 |
1 0 |
0 |
1 |
1 |
0 |
|
1 0 |
1 |
0 |
0 |
1 |
82

13. |
|
|
|
|
14. |
|
|
|
|
|
x3, x4 |
|
|
|
|
x3, x4 |
|
|
|
x1, x2 |
0 0 0 1 1 1 1 0 |
x1, x2 |
0 0 0 1 1 1 1 0 |
||||||
0 0 |
0 |
0 |
1 |
0 |
0 0 |
1 |
0 |
1 |
1 |
0 1 |
0 |
1 |
1 |
0 |
0 1 |
1 |
0 |
0 |
1 |
1 1 |
1 |
0 |
0 |
0 |
1 1 |
1 |
0 |
0 |
1 |
1 0 |
1 |
0 |
0 |
1 |
1 0 |
0 |
0 |
0 |
1 |
15. |
|
|
|
|
16. |
|
|
|
|
|
x3, x4 |
|
|
|
|
x3, x4 |
|
|
|
x1, x2 |
0 0 0 1 1 1 1 0 |
x1, x2 |
0 0 0 1 1 1 1 0 |
||||||
0 0 |
1 |
0 |
1 |
1 |
0 0 |
1 |
1 |
0 |
1 |
0 1 |
0 |
1 |
0 |
0 |
0 1 |
1 |
0 |
0 |
1 |
1 1 |
0 |
0 |
1 |
0 |
1 1 |
0 |
1 |
0 |
1 |
1 0 |
1 |
0 |
0 |
1 |
1 0 |
1 |
0 |
0 |
1 |
17. |
|
|
|
|
18. |
|
|
|
|
|
x3, x4 |
|
|
|
|
x3, x4 |
|
|
|
x1, x2 |
0 0 0 1 1 1 1 0 |
x1, x2 |
0 0 0 1 1 1 1 0 |
||||||
0 0 |
1 |
0 |
1 |
1 |
0 0 |
1 |
0 |
0 |
0 |
0 1 |
0 |
0 |
1 |
1 |
0 1 |
1 |
0 |
1 |
0 |
1 1 |
1 |
0 |
1 |
0 |
1 1 |
1 |
1 |
0 |
1 |
1 0 |
0 |
0 |
1 |
0 |
1 0 |
1 |
1 |
1 |
1 |
19. |
|
|
|
|
20. |
|
|
|
|
|
x3, x4 |
|
|
|
|
x3, x4 |
|
|
|
x1, x2 |
0 0 0 1 1 1 1 0 |
x1, x2 |
0 0 0 1 1 1 1 0 |
||||||
0 0 |
1 |
1 |
0 |
1 |
0 0 |
1 |
1 |
0 |
1 |
0 1 |
1 |
0 |
0 |
1 |
0 1 |
1 |
1 |
0 |
0 |
1 1 |
0 |
1 |
1 |
0 |
1 1 |
1 |
1 |
1 |
0 |
1 0 |
1 |
0 |
0 |
1 |
1 0 |
1 |
0 |
0 |
1 |
В задании 5 составить таблицу Поста и найти базисы из следующих функций.
1.(x y z , (xy) + z, x y , x+ y + yx, x (y x)).
2.(x + yz , x (x y), zx (x yz), x (y + z )).
3.(x (y z), x(x + y), (x z) y, x | (y x)).
4.(x + y z, x (y x), (x | x) | (y | y), x yz).
5.((xy) z, xy x, y + xz, x+ y, x (yz)).
6.(x y y z , x y , x| (y| x ), x (yx), x + xy).
7.(x (yz), x y z , x + (y z), x | x, x (y + x)).
8.(x + yz, (00010111), x y z , y x + y x , x x)).
83

9.(xy z, x ~ (y+xz), (11010100), yx+ z, (xy) | x).
10.(x+ (y ~ x), y (xz), (00101011), x (y | z), x+ y).
11.x+( y z ), (x|y) + z, (x y )+ z, x+ y + yx, (x y) (y x).
12.(x ~ yz , x (x|y), (z+ x) (x+ yz), xz (y + z )).
13.(x (y + z), x~(x + y), x|y z y, x | (y x)).
14.(x + y + z, x~(y x), y+((x | x) | (y | y)), (x y)|z).
15.((x+ y)| z, (x+ y) x, y~(x~z), x y, x (y+z)).
16.((x+ y ) y z , 1+ x y , x|(y| x ), x (yx), x + xy).
17.(x (yz), x y z , x + (y z), x | x, x (y + x)).
18.(x~ yz, (01010111), x +( y | z ), (y x) + y x , x x)).
19.((x+y) z, z ~ (y+ xz), (10010110), yxz+ z, (xy) x).
20.(z+ (y ~ z), x (yz), (01010111), x (z | y), x+ y+z).
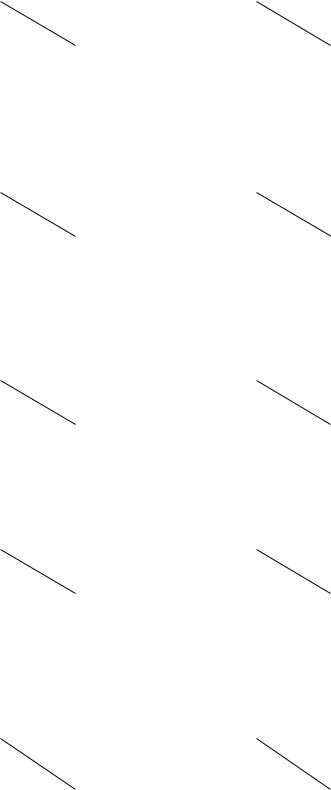
В задании 6: а) требуется составить структурную матрицу для данного орграфа (или графа) и методами булевой алгебры найти все пути Pij из вершины i в вершину j, затем найти все сечения Sij между этими вершинами. Мы в данном задании (чтобы исключить возможные неясности графического рисунка) указываем все ориентированные ребра, причем запись (2–4) означает, что из 2-й вершины есть ребро в 4-ю, а обратной связи нет. Напомним, что для нахождения путей из вершины i в вершину j нужно раскрывать минор структурной матрицы Мij (т. е. вычеркнyть из струк-
турной матрицы строчку с номером j и столбец с номером i). Сечения же находятся отрицанием путей (т. е.конъюнкция меняется на дизъюнкцию и наоборот).
б) составить матрицу смежности С данного графа, возвести ее в квадрат и найти тот элемент матрицы С3, который укажет, сколько путей длины 3 найдется в данном графе между данными вершинами; сверить полученный результат с результатом выполнения пункта а.
1. Дан орграф. Имеется 2 ориентированных ребра: (2–5) и (3–4); i = 3, j = 1.
|
2 |
b |
3 |
h |
a |
f |
|
|
c |
1 |
|
|
|
4 |
d |
5 |
e |
|
|
2. Дан орграф. Имеетcя 2 ориентированных ребра (2–3) и (2–4). i = 4, j = 6.
84
2 |
a |
3 |
|
b |
c |
|
d |
e |
|
f |
|
1 |
|
h |
6 |
g |
|
|
|
4 |
k |
5 |
|
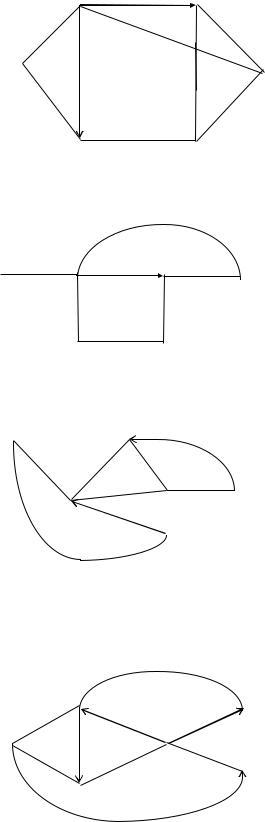
3. Дан орграф. Имеется 1 ориентированное ребро: (4–5); i = 3, j = 4.
d
1 |
a |
4 |
b |
5 |
c |
6 |
|
|
e |
|
f |
|
|
|
|
2 |
g |
3 |
|
|
4.Дан орграф. Имеется 2 ориентированных ребра: (6–2) и (5–4);
i= 3, j = 5.
1 |
|
2 |
|
|
|
b |
|
c |
d |
|
e |
h |
4 |
а |
3 |
f |
6 |
|
|
g
5
5.Дан орграф. Имеется 3 ориентированных ребра: (3–2), (2–5) и (1–6);
i= 3, j = 1.
|
|
a |
|
|
2 |
|
4 |
b |
|
d |
e |
1 |
|
|
3 |
f |
c g |
|
h |
|
5 |
|
6 |
k
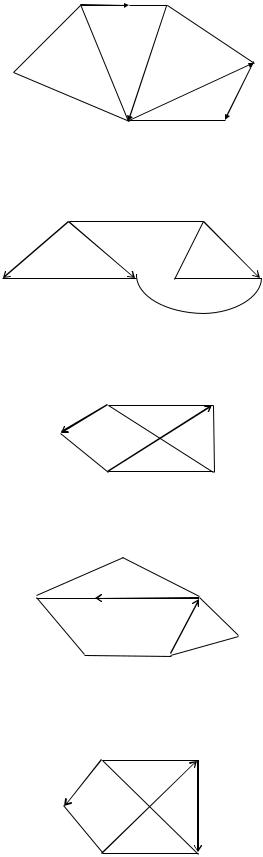
6. Дан орграф. Имеется 4 ориентированных ребра: (2–3), (3–5), (5–4) и (4–6); i = 3, j = 2.
85
2 |
a |
3 |
|
b |
c |
d |
e |
1 |
|
|
4 |
f |
|
g |
h |
|
5 |
|
|
|
|
k |
6 |
7.Дан орграф. Имеется 3 ориентированных ребра: (2–1), (2–3) и (4–5);
i= 2, j = 4.
|
2 |
a |
|
4 |
|
b |
c |
|
d |
|
e |
1 |
f |
3 |
6 |
h |
5 |
|
|
|
|
k |
|
8. Дан орграф. Имеется одно ориентированное ребро: (5–3); i = 3, j = 1.
|
2 |
a |
3 |
1 b |
|
c d |
e |
f |
|
|
|
5 |
g |
|
4 |
9. Дан орграф. Имеется 2 ориентированных ребра: (2–3) и (5–2). i = 4, j = 6.
|
1 |
|
|
|
|
a |
b |
|
|
3 |
c |
|
|
2 |
|
e |
|
f |
d |
|
|
|
g |
6 |
|
4 |
h |
5 |
|
10.Дан орграф. Имеется 3 ориентированных ребра: (2–1), (4–3), (3–5);
i= 2, j = 4.
2 |
a |
3 |
b |
c |
d |
1 |
|
e |
f |
|
|
4 |
h |
5 |
86
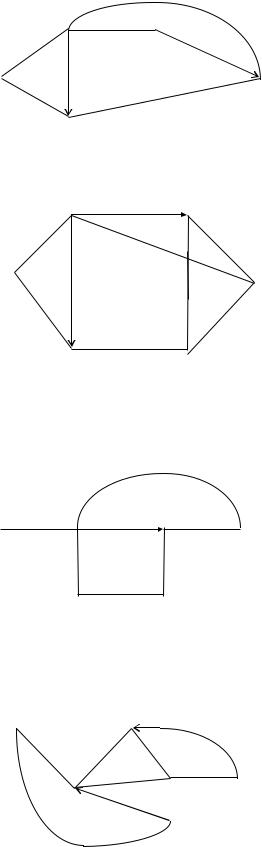
11. Дан орграф. Имеется 2 |
ориентированных ребра: (2–5) и (3–4); |
|||
i = 1, j = 4. |
|
|
|
|
|
2 |
b |
3 |
h |
a |
f |
|
|
c |
1 |
d |
|
|
4 |
5e
12.Дан орграф. Имеетcя 2 ориентированных ребра (2–3) и (2–4). i = 3,
j = 4.
|
2 |
a |
|
3 |
|
b |
c |
|
d |
1 |
e |
|
f |
6 |
|
g |
|
|
h |
|
4 |
k |
5 |
|
13. Дан орграф. Имеется 1 ориентированное ребро: (4–5); i = 6, j = 2.
|
|
|
|
d |
|
|
1 |
a |
4 |
b |
5 |
c |
6 |
|
|
e |
|
f |
|
|
|
|
2 |
g |
3 |
|
|
14. Дан орграф. Имеется 2 |
ориентированных ребра: (6–2) и (5–4); |
|||
i = 1, j = 6. |
|
|
|
|
1 |
2 |
|
|
e |
b |
c |
d |
|
|
4 |
g |
3 |
f |
6 |
h |
а |
5 |
|
|
87
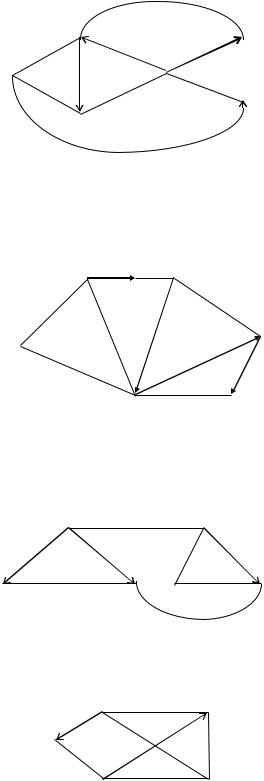
15.Дан орграф. Имеется 3 ориентированных ребра: (3–2), (2–5) и (1–6);
i= 1, j = 3.
|
|
a |
|
|
2 |
|
4 |
|
b |
d |
e |
1 |
c |
|
3 |
|
f |
g |
h |
|
5 |
|
6 |
k
16.Дан орграф. Имеется 4 ориентированных ребра: (2–3), (3–5), (5–4)
и(4–6); i = 1, j = 6.
2 |
a |
3 |
|
b |
c |
d |
e |
1 |
|
|
4 |
f |
|
g |
h |
|
5 |
k |
6 |
17. Дан орграф. Имеется 3 ориентированных ребра: (2–1), (2–3) и (4–5); i = 4, j = 2.
|
2 |
a |
|
4 |
|
b |
c |
|
d |
|
e |
1 |
f |
3 |
6 |
h |
5 |
|
|
|
|
k |
|
18. Дан орграф. Имеется одно ориентированное ребро: (5–3); i = 4, j = 2.
|
|
2 |
a |
3 |
1 |
b |
c |
d |
e |
|
f |
|
|
|
|
|
5 |
g |
4 |
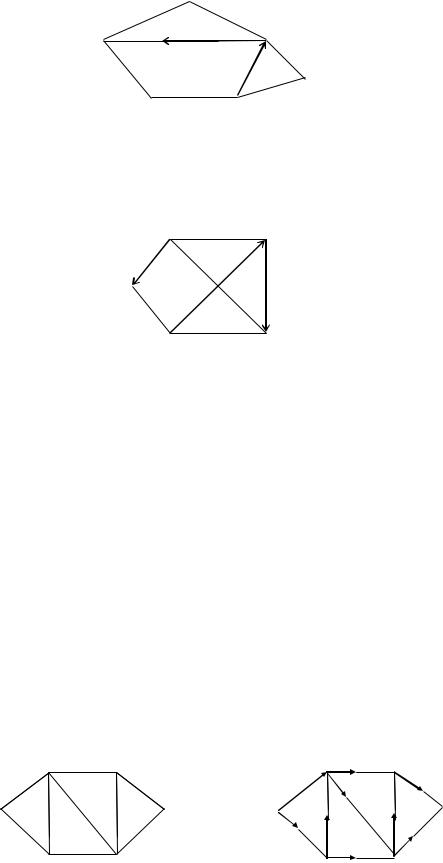
19. Дан орграф. Имеется 2 ориентированных ребра: (2–3) и (5–2). i = 5, j = 1.
88
|
|
1 |
|
|
a |
b |
|
3 |
c |
|
2 |
|
e |
f |
d |
|
|
g |
6 |
4h 5
20.Дан орграф. Имеется 3 ориентированных ребра: (2–1), (4–3), (3–5);
i= 5, j = 2.
2 |
a |
3 |
b |
c |
d |
1 |
|
e |
f |
|
|
4 |
h |
5 |
В задани 7 требуется найти в данной сети (т. е. в графе с заданными пропускными способностями ребер) максимальный поток из вершины с номером 1 в вершину с наибольшим номером (в наших заданиях либо вершину 5, либо 6). В заданиях заданы 2 графа (граф, который находится слева – это сеть с заданными пропускными способностями ребер; граф справа – с заданным потоком, который необходимо либо улучшить, либо доказать, что он неулучшаем и, значит, является максимальным). Задание
вэтих примерах состоит в следующем: требуется, расставляя пометки
вграфе с заданным потоком с помощью алгоритма, описанного в теореме Форда – Фалкерсона, найти максимальный поток между вершиной с номером 1 и вершиной с максимальным номером. При этом, если улучшенный поток окажется максимальным, то нужно указать то минимальное сечение, которому равен наш поток (если же улучшенный поток не окажется максимальным, то нужно снова его улучшать до тех пор, пока он
не окажется максимальным).
1.
|
|
2 |
5 |
3 |
|
|
2 |
5 |
|
3 |
|
|
15 |
|
|
|
8 |
|
3 |
|
|
|
8 |
1 |
4 |
|
7 |
3 |
6 |
1 |
4 |
|
2 |
3 |
6 |
|
10 |
|
|
15 |
|
|
10 |
|
|
|
5 |
|
4 |
12 |
|
5 |
|
|
4 |
6 |
|
5 |
|
89
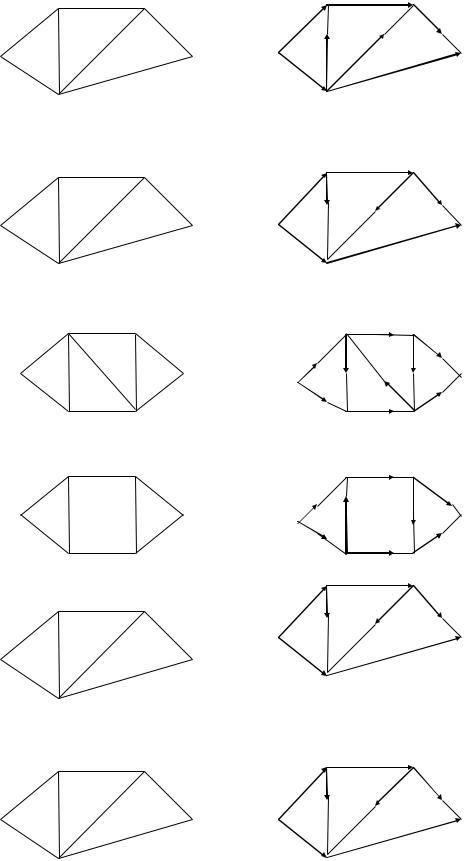
2.
|
2 |
11 |
3 |
|
2 |
11 |
|
3 |
15 |
3 |
8 |
16 |
|
7 |
3 |
3 |
13 |
1 |
|
|
|
5 |
1 |
|
|
5 |
|
8 |
6 |
|
|
8 |
|
2 |
|
|
4 |
|
|
|
4 |
|
|
|
3.
|
2 |
10 |
3 |
|
2 |
7 |
3 |
|
10 |
3 |
8 |
10 |
|
10 |
3 |
3 |
4 |
1 |
|
|
|
5 |
1 |
|
|
5 |
12 |
|
|
11 |
|
5 |
|
11 |
|
|
4 |
|
|
|
4 |
|
|
|
4.
|
2 |
7 |
|
3 |
|
|
|
2 |
7 |
3 |
|
|
1 |
15 |
2 |
10 |
7 |
5 |
6 |
5 |
2 |
4 |
2 |
5 |
6 |
|
7 |
|
|
|
20 |
|
1 |
7 |
|
7 |
|
|
|
4 |
9 |
|
5 |
|
|
|
4 |
9 |
5 |
|
|
5.
|
2 |
|
8 |
3 |
20 |
|
|
2 |
8 |
3 |
|
1 |
30 |
7 |
|
|
3 |
6 |
7 |
1 |
3 |
5 |
6 |
|
4 |
|
|
|
6 |
|
1 |
4 |
6 |
|
|
|
|
4 |
15 |
5 |
|
|
|
4 |
3 |
5 |
|
6.
|
2 |
12 |
3 |
|
|
2 |
6 |
3 |
|
10 |
4 |
|
5 |
16 |
|
10 |
4 |
2 |
16 |
1 |
|
|
|
|
5 |
1 |
|
|
5 |
18 |
|
|
13 |
|
|
7 |
|
|
13 |
|
4 |
|
|
|
|
|
4 |
|
|
7.
|
2 |
15 |
3 |
|
|
2 |
6 |
3 |
10 |
6 |
3 |
20 |
|
10 |
4 |
3 |
3 |
1 |
20 |
|
|
5 |
1 |
5 |
|
5 |
|
4 |
12 |
|
|
|
4 |
12 |
|
90
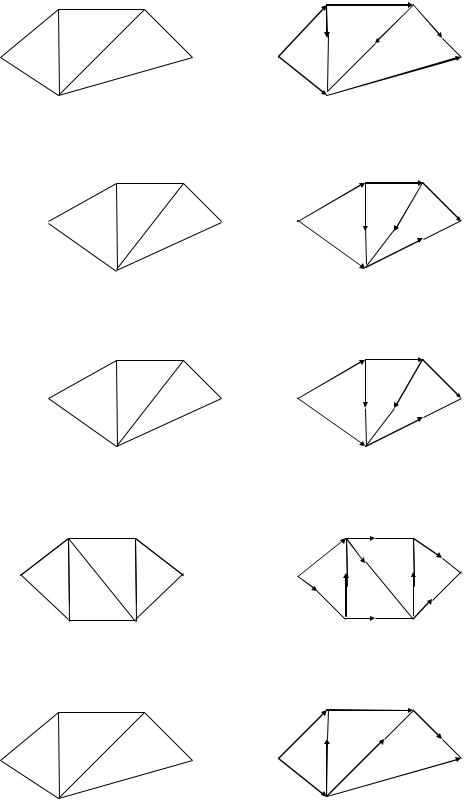
8.
|
2 |
14 |
3 |
|
|
2 |
10 |
3 |
16 |
12 |
8 |
20 |
|
16 |
6 |
6 |
4 |
1 |
|
|
|
5 |
1 |
|
|
5 |
25 |
|
|
14 |
|
2 |
|
|
14 |
|
4 |
|
|
|
|
4 |
|
|
9.
|
2 |
5 |
3 |
|
|
2 |
5 |
3 |
8 |
3 |
6 |
30 |
|
8 |
3 |
2 |
3 |
1 |
|
|
|
6 |
1 |
|
|
6 |
20 |
|
|
11 |
|
6 |
|
|
11 |
|
4 |
|
|
|
|
4 |
|
|
10.
2 |
20 |
3 |
|
|
2 |
6 |
3 |
|
8 |
2 |
3 |
25 |
|
8 |
2 |
3 |
3 |
1 |
|
|
|
5 |
1 |
|
|
5 |
30 |
|
9 |
|
|
4 |
|
9 |
|
|
4 |
|
|
|
|
4 |
|
|
11.
|
2 |
7 |
3 |
|
|
2 |
7 |
|
3 |
|
13 |
|
|
|
10 |
|
5 |
|
|
|
10 |
1 |
4 |
7 |
3 |
6 |
1 |
4 |
|
2 |
3 |
6 |
11 |
|
|
|
16 |
|
11 |
|
|
|
6 |
|
4 |
12 |
5 |
|
|
4 |
7 |
|
5 |
|
12.
|
2 |
10 |
3 |
|
2 |
10 |
|
3 |
17 |
3 |
8 |
16 |
|
7 |
3 |
3 |
13 |
1 |
|
|
|
5 |
1 |
|
|
5 |
8 |
|
|
6 |
|
8 |
|
|
2 |
|
4 |
|
|
|
4 |
|
|
|
91
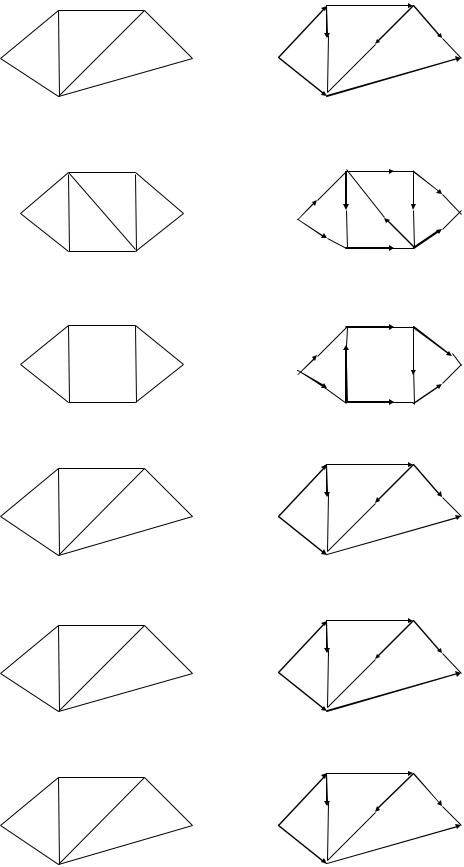
13.
|
2 |
10 |
3 |
|
|
2 |
7 |
3 |
15 |
3 |
8 |
10 |
|
15 |
8 |
3 |
4 |
1 |
|
|
|
5 |
1 |
|
|
5 |
12 |
|
|
11 |
|
5 |
|
|
16 |
|
4 |
|
|
|
|
4 |
|
|
14.
|
2 |
|
9 |
3 |
|
|
|
2 |
9 |
3 |
|
1 |
15 |
2 |
10 |
7 |
5 |
6 |
7 |
2 |
4 |
2 7 |
6 |
|
9 |
|
|
|
|
20 |
1 |
9 |
|
9 |
|
|
4 |
|
11 |
5 |
|
|
|
4 |
11 |
5 |
|
15.
|
2 |
|
8 |
3 |
20 |
|
|
2 |
10 |
3 |
|
1 |
30 |
7 |
|
|
3 |
6 |
9 |
1 |
3 |
7 |
6 |
|
4 |
|
|
|
|
6 |
1 |
4 |
|
|
6 |
|
|
4 |
15 |
|
5 |
|
|
4 |
3 |
5 |
|
16.
|
2 |
12 |
3 |
|
2 |
8 |
|
3 |
12 |
4 |
5 |
16 |
|
12 |
4 |
2 |
6 |
1 |
|
|
|
5 |
1 |
|
|
5 |
18 |
|
|
13 |
|
7 |
|
|
13 |
|
4 |
|
|
|
4 |
|
|
|
17.
|
|
2 |
15 |
3 |
|
|
2 |
10 |
3 |
|
15 |
8 |
3 |
20 |
|
15 |
5 |
3 |
7 |
1 |
20 |
|
|
|
5 |
1 |
5 |
|
5 |
|
|
4 |
12 |
|
|
|
4 |
13 |
|
18.
2 |
14 |
|
3 |
|
|
2 |
10 |
3 |
20 |
12 |
8 |
20 |
|
16 |
6 |
6 |
4 |
1 |
|
|
5 |
1 |
|
|
|
5 |
20 |
|
|
14 |
|
2 |
|
|
14 |
4 |
|
|
|
|
|
4 |
|
|
92
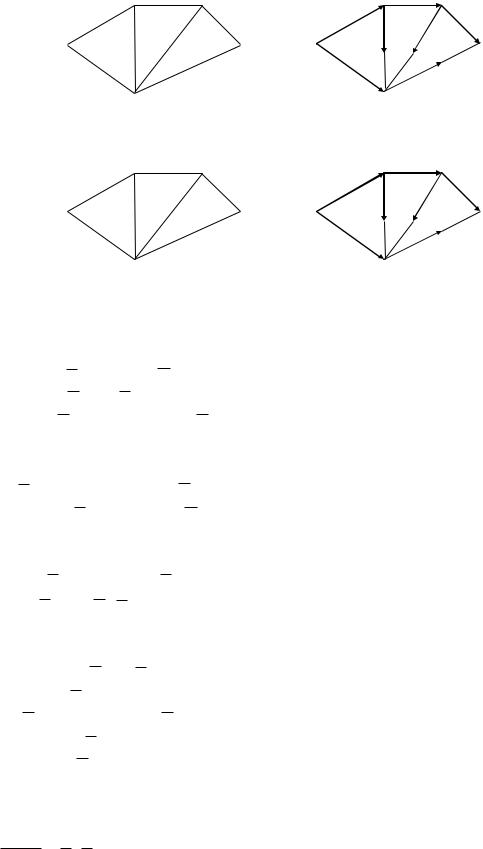
19.
|
2 |
7 |
3 |
|
|
2 |
7 |
3 |
|
10 |
3 |
6 |
30 |
|
10 |
|
3 |
4 |
3 |
1 |
|
|
6 |
1 |
|
|
|
|
6 |
20 |
|
11 |
|
|
6 |
|
|
13 |
|
|
4 |
|
|
|
|
4 |
|
|
|
20. |
|
|
|
|
|
|
|
|
|
|
2 |
15 |
3 |
|
2 |
|
6 |
3 |
|
10 |
2 |
3 |
25 |
|
8 |
2 |
|
3 |
3 |
1 |
|
|
5 |
1 |
|
|
|
|
5 |
20 |
|
|
9 |
|
6 |
|
|
|
11 |
|
4 |
|
|
|
|
4 |
|
|
|
Задание 8: «Oперации над множествами».
На множестве U = {1, 2, 3, 4} заданы подмножества А = {1, 3, 4},
В= {2, 3}, С = {1, 4}. Перечислить элементы множества.
1.А · В; А + A ; В\А; А C + В.
2.А · С; B + A ; (В\ A ) + С.
3.(А · В) + A ; А · (В + С); А\ B .
На множестве U = {1, 2, 3, 4} заданы подмножества А = {1, 2}, В = {2, 3},
С= {1, 3}. Перечислить элементы множества.
4.А · B ; А + В + С; А\(В · C ).
5.А + B С; A · С; (А\В) + C .
На множестве U = {1, 2, 3, ..., 10} заданы подмножества А = {2, 4, 6, 8},
В= {3, 6, 9}. Перечислить элементы множества.
6.А + В; A · В; А\B; А + B .
7.А · В; A + B; A B ; В\А.
На множестве U = {а, б, в, г} заданы подмножества А ={а, в}, В = {а, б, г}
иС = {б, в}. Перечислить элементы множества.
8.А · В; A B C ; А\ B .
9.А + В; A A ; В\С; А · В + С.
10.А · C ; (А + В) · С; В\ C .
11.А + С; (А · B ) + С; В\А.
12.В · С; (А · C ) + B; С\А.
Доказать равенства.
13.(А + В) · С = (А · С) + (В · С).
14.А + (B · C) = (A + B) · (A + C).
15.A B А В.
93

16.A B А В.
17.А\(B\C) = A\(B + C).
18.А + (А · В) = А.
19.А\B = А · B .
20.А + ( A · В) = А + В.
21.(А · В) + (А · B ) = А.
22.(А · B ) + ( A · В) + (А · В) = А + В.
23.Если А В, то А + В = В.
24.Если А В, то А · В = А.
25.А\(А · В) = А · B .
Задание 9: «Функции».
Определить, являются ли указанные бинарные отношения R функциями.
1.R = {(1, 1), (1, 2), (2, 4), (3, 6)}.
2.R = {(1, 1), (2, 4), (3, 4)}.
3.R a1,b1 , a2 ,b2 , a3,b3 . Бинарное отношение R определено на де-
картовом произведении множеств А × В, где А = a1, a2 , a3 , В = b1,b2 ,b3 .
4.R = { x y4 , где x, y R }.
5.Бинарное отношение R задано на декартовом произведении множеств В Р, где множество книг в книжном магазине обозначим B, а множество цен на эти книги обозначим P. Пара (х,у) R, т. е. хRу, тогда и только тогда, когда книга х имеет цену у.
Определить, являются ли указанные функции сюръективными, инъективными, биективными.
6.y x2 , x 2, 0 y 4 .
7.y x2 , x 2, y R .
8.y x2 , 0 x 2, 0 y 4 .
9.y x2 , 1 x 2, 0 y 5 .
10.f : [0,1] →[0,3], y 3 sin 1 x .
2
11.f : [0,1] →[0,3], y 12 x 1 2
.2
12. f : [0,1] →[0,3], y 3x.
Указать область определения и область значений функции.
13.{(1,1),(2,4),(3,4)}.
14.y 1 2x .
94
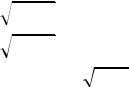
15.y 
 1 x2 .
1 x2 .
16.y 
 x2 1.
x2 1.
17.y lg 3 n 
 1 n, n N.
1 n, n N.
Указать область определения функции.
18.y x2 , 0 y 1.
19.y x2 , 1 y 4.
20.y x2 , 0,01 y 0,25.
21.y sin x, 0 y 1.
22.y sin x, 1 y 0.
23.y cos x, 0 y 1.
24.y cos x, 1 y 0.
Указать область значений функций. 25. y x, 2 x 1,
y x2 , 3 x 1,5 0 y 2.
Задание 10: «Бинарные отношения»
Отношение задано на указанном множестве. Для каждого отношения нужно:
а) проверить, является ли отношение рефлексивным, антирефлексивным, симметричным, асимметричным, антисимметричным, транзитивным,
б) построить матрицу смежности и граф отношения, в) определить, является ли заданное отношение отношением эквива-
лентности, для отношения эквивалентности построить классы эквивалентности.
1.На множестве А = {1, 2, 3, 4, 5, 6} задано отношение делимости: хRу тогда и только тогда, когда х делится на у.
2.На множестве А = {1, 2, 3, 4, 5, 6} задано отношение делимости: хRу тогда и только тогда, когда у делится на х.
3.На множестве А = {1, 2, 3, 4, 5, 6} задано отношение взаимной простоты: хRу тогда и только тогда, когда х и у взаимно просты, т. е. их наибольший общий делитель равен 1.
4.На множестве А = {1, 2, 3, 4, 5, 6, 7} задано отношение взаимной простоты: хRу тогда и только тогда, когда х и у взаимно просты, т. е. их наибольший общий делитель равен 1.
5.На множестве А = {53, 43, 42, 44, 50, 20} задано отношение сравнимости по модулю три (mod 3): хRу тогда и только тогда, когда х и у имеют одинаковые остатки от деления на 3.
6.На множестве А = {53, 43, 42, 44, 50, 20} задано отношение R: хRу тогда и только тогда, когда в наборе имеется элемент больший х, но меньший у.
95

7. На множестве А = {53, 43, 42, 44, 50, 20} задано отношение R: хRу тогда и только тогда, когда в наборе имеется элемент z, такой что
(х z)(y z) < 0.
8.На множестве А = {53, 43, 42, 44, 50, 20} задано отношение R: хRу тогда и только тогда, когда каждая из цифр числа х больше цифры числа у, стоящей в соответствующем разряде.
9.На множестве А = {53, 43, 42, 44, 50, 20} задано отношение R: хRу тогда и только тогда, когда каждая из цифр числа х меньше цифры числа у, стоящей в соответствующем разряде.
10. На множестве А = {53, 43, 42, 44, 50, 20} задано отношение R: хRу
тогда и только тогда, когда x y 5.
11.На множестве А = {60, 25, 71, 68, 20, 24} задано отношение сравнимости по модулю три (mod 3): хRу тогда и только тогда, когда х и у имеют одинаковые остатки при делении на 3.
12.На множестве А = {60, 25, 71, 68, 20, 24} задано отношение R: хRу тогда и только тогда, когда в наборе имеется элемент больший х, но меньший у.
13.На множестве А = {60, 25, 71, 68, 20, 24} задано отношение R: хRу тогда и только тогда, когда в наборе имеется элемент z, такой что (х – z)
(y z) ≤ 0.
14.На множестве А = {60, 25, 71, 68, 20, 24} задано отношение R: хRу тогда и только тогда, когда каждая из цифр числа х больше цифры числа у, стоящей в соответствующем разряде.
15.На множестве А = {60, 25, 71, 68, 20, 24} задано отношение R: хRу тогда и только тогда, когда каждая из цифр числа х меньше цифры числа у, стоящей в соответствующем разряде.
16.На множестве А = {60, 25, 71, 68, 20, 24} задано отношение R: хRу
тогда и только тогда, когда x y 5.
17.На множестве А = {1, 2, 3, 4, 5, 6} задано отношение R: хRу тогда и только тогда, когда х и у имеют общий делитель, отличный от 1.
18.На множестве А = {1, 2, 3, 4, 5, 6} задано отношение R: хRу тогда и
только тогда, когда x y четное число.
19.На множестве А = {1, 2, 3, 4, 5, 6} задано отношение R: хRу тогда и только тогда, когда (х + у) четное число.
20.На множестве А = {1, 2, 3, 4, 5} задано отношение R: хRу тогда и только тогда, когда х является делителем х + у.
21.На множестве А = {3, 4, 5, 6, 7} задано отношение R: хRу тогда и только тогда, когда х является делителем (х + у).
22.На множестве А = {3, 4, 5, 6, 7} задано отношение R: хRу тогда и
только тогда, когда x y 3.
96
23.В семье 5 детей: сыновья Андрей, Борис и Вадим, дочери Галина и Дарья. На этом множестве детей задано отношение R «брат»: хRу тогда и только тогда, когда х приходиться братом у.
24.У главы семьи Андрея два сына – Борис и Вадим. У Бориса два сына – Григорий и Дмитрий, у Вадима – сын Егор. На этом множестве всех мужчин семьи задано отношение R «сын»: хRу тогда и только тогда, когда
хприходиться сыном у.
25.У директора фирмы Д. есть два заместителя Зам. 1 и Зам. 2. У первого заместителя Зам. 1 есть два подчиненных ему референта Реф. 1 и Реф. 2, у второго заместителя Зам. 2 есть подчиненный ему ассистент Ас. На этом множестве сотрудников фирмы задано отношение R «начальник и подчиненный»: хRу тогда и только тогда, когда х является начальником у.
Задание 11: «Сравнение множеств».
В предлагаемых ниже задачах требуется установить взаимнооднозначное соответствие между двумя данными множествами X и Y и (или) установить, являются ли они конечными, счетными или имеют мощность континуума.
1.Х – окружность, Y – две окружности;
2.X – окружность, Y – прямая;
3.X – множество «счастливых» 6-значных автобусных билетов, у которых сумма цифр, стоящих в первых 3 разрядах, равна сумме цифр, стоящих в последних трех разрядах, Y – множество 6-значных автобусных билетов, у которых сумма всех цифр равна 27;
4.X – множество точек разрыва возрастающей нa [0, 1] функции, Y – множество комплексных чисел, у которых и вещественная и мнимая часть являются целыми числами.
5.Найти мощность множества всех букв «Г», которые можно расположить на плоскости так, чтобы никакие две из них не пересекались.
6.Найти мощность множества всех букв «Т», которые можно расположить на плоскости так, чтобы никакие две из них не пересекались.
7.X – множество всех десятизначных чисел, у которых сумма цифр, стоящих на четных местах, равна сумме цифр, стоящих на нечетных местах, Y – множество десятизначных чисел, у которых сумма всех цифр равна 50.
8.X – множество точек квадрата [0, 1]2, Y – множество точек тре-
угольника с вершинами А(0, 0), В(1, 0), С(0, 1).
9.X: [0, 1]2; Y: [0, 1]2 × [0, 1]2.
10.Найти мщность множества всех конечных подмножеств натурального ряда.
11.Найти мощность множества всех точек разрыва функции, заданных на [0, 10] и имеющих там ровно один минимум.
97
