ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ

им. проф. М. А. БОНЧ-БРУЕВИЧА»

Ю. Б. ФАРФОРОВСКАЯ, О. М. ДМИТРИЕВА, Е. Л. РАБКИН, Н. К. ЯНОВСКАЯ

ДИСКРЕТНАЯ МАТЕМАТИКА

Учебно-методическое пособие по выполнению контрольных работ

САНКТ-ПЕТЕРБУРГ

2014

3

1.ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

1.1.Основные понятия и определения

1.Предварительные замечания.

В каждой математической дисциплине есть неопределяемые понятия, т. е. понимаемые интуитивно. Это естественно: ведь определения объясняют смысл одних слов через другие слова, но слов – конечное число, и если где-то не остановиться, то мы попадем в порочный круг, т. е. будем объяснять слова через них же самих. Например, в геометрии неопределяемы понятия «точка», «прямая», «плоскость». Есть менее очевидные неопределяемые понятия, например понятия «принадлежит», «между» и др. В теории множеств неопределяемыми понятиями являются «множество»,

«элемент множества», «принадлежит». Для них можно лишь подобрать синонимы. Например, синонимами понятия «множество» являются понятия «набор», «система», «ансамбль», «совокупность» и т. д. Элементы множества иногда называют его точками. Тот факт, что элемент х принадлежит множеству М обозначается символом, x M , что не принадлежит – символом x M или x M . Если каждый элемент множества В является одновременно элементом множества А, то множество В называется подмножеством множества А, и этот факт обозначают символом B A или A B. Множества А и В называют равными и пишут А = В, если одновременно B A и A B, т. е. если они состоят из одних и техже элементов.

Пустым множеством называют множество, не содержащее ни одного элемента, и обозначают его . У каждого множества есть два подмножества, которые называют несобственными. Это – само исходное множество и пустое множество. Все остальные подмножества называют собственными.

2. Операции над множествами.

Определения. (Все определения будем иллюстрировать на примере двух подмножеств А = {1, 3, 5} и B = {4, 5, 6} множества U ={1, 2, 3, 4, 5, 6}).

Дополнением A подмножества А множества U называют множество точек U, не принадлежащих множеству А. Это аналог отрицания в булевой алгебре.

Например, A ={2, 4, 6}, B = {1, 2, 3}. Объединением (суммой) А + В = А В

множеств А и В называют множество точек из U, каждая из которых принадлежит хотя бы одному из множеств А или В. Это аналог дизъюнкции в булевой алгебре. Например, А В = {1, 3, 4, 5, 6}, А B = {1, 2, 3, 5}.

n

Объединением (суммой) А1 + А2 + … + Аn = Ak n множеств А1, А2, …, Аn

1

называют множество точек из U, каждая из которых принадлежит хотя бы одному из множеств А1, А2, …, Аn. Пересечением (произведением) A · В = А В

множеств А и В называют множество точек из U, каждая из которых при-

4

надлежит обоим множествам А и В. Это аналог конъюнкции в булевой ал-

гебре. Например, А В={5}, А B = {1, 3}. Пересечением (произведением)

n

А1·А2·…·Аn= Ak n множеств А1, А2, …, Аn называют множество точек U,

1

каждая из которых принадлежит одновременно всем множествам А1, А2,

…, Аn.

Два множества А и В называют непересекающимися, если А · В = . Разностью А\B множеств А и В называют множество точек А, не при-

надлежащих множеству В. Это аналог импликации в булевой алгебре. Очевидно, что А\B=А B . Например, А\B={1, 3}= А B .

Замечание. Очевидно, что для любого подмножества А справедливы равенства A A , A A U , и эти равенства полностью характеризуют дополнение множества А до множества U.

Определение. Прямым (декартовым) произведением А В множеств А и В называется множество всех упорядоченных пар , где первый элемент принадлежит множеству А, а второй множеству В: А×В ={(а,b), где а А, b В}. Аналогично определяется произведение нескольких множеств: А1 × А2 × А3 ×…× Аn есть совокупность всевозможных упорядоченных на-

боров из п элементов {a1, a2, …, an}, где а1 А1, а2 А2, …, аn Аn. Каждый такой набор элементов называется кортежем. Произведение множества са-

мого на себя называется квадратом множества и обозначается так: А2= А × А,

аналогично куб А – это А3= А × А × А, …, п-ая степень А – это Аn= А × А ×

…× А.

Например, если А – множество из трех собак: А = {с1, с2, с3}, а множество В состоит из двух кошек: В = {k1, k2}, то А × В есть множество из шести пар: А × В = {(с1, k1), (с2, k1), (с3, k1), (с1, k2), (с2, k2), (с3, k2)},

а В × А={(k1, с1), (k1, с2), (k1, с3), (k2, с1), (k2, с2), (k2, с3)}. Примером прямо-

го произведения множеств является также таблица соревнований, когда каждая команда встречается с каждой. В таблице чемпионата России по футболу каждая игра отмечена как упорядоченная пара футбольных команд, причем первая в паре – та, на чьем поле состоится игра, а это и есть прямое произведение множества А (состоящего из всех команд первенства) самого на себя, т. е. А2. Произведение отрезка [0, 1] самого на себя, т. е. [0, 1]2= [0, 1] × [0, 1] есть множество всевозможных упорядоченных пар чисел (х, у), х [0, 1], у [0, 1], что можно интерпретировать как множество точек на плоскости, образующее квадрат. Аналогично, [0, 1]3= [0, 1] × [0, 1] × [0, 1] – это куб, и т. д. Произведение числовой прямой R самой на себя, т. е. R2 –

5

это плоскость, а R × R × R = R3 – это все трехмерное пространство. Если

А = {3, 8}, В = {a, b, c}, то А × В = {(3, a), (3, b), (3, c), (8, a), (8, b), (8, c)}, а если А = {3, 8}, то А × А = А2= {(3, 3), (3, 8), (8, 3), (8, 8)}.

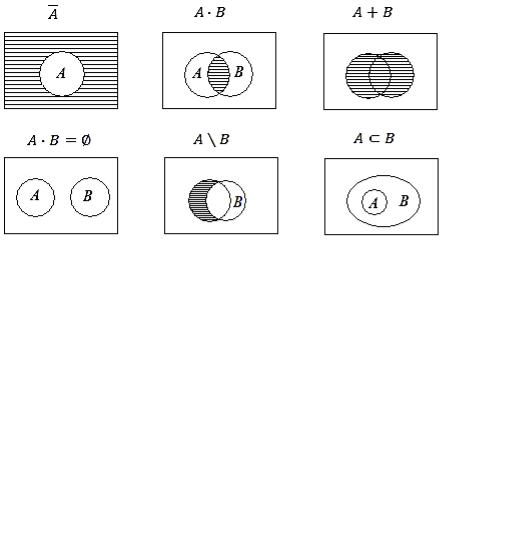
Операция А × В не коммутативна, не ассоциативна, но дистрибутивна. Диаграммы Эйлера − Венна. На диаграммах Эйлера – Венна множество U изображается прямоугольником, а множества А, В, С, … – областями

внутри прямоугольника. На рис. 1.1 проиллюстрированы введенные определения операций над множествами.

Рис. 1.1

3. Cвойства операций над множествами

Алгебра множеств – это пример булевой алгебры, поэтому все указанные свойства операций следуют из свойств дизъюнкции, конъюнкции и отрицания. Заметим, что на диаграмме Эйлера – Венна можно представить и другие логические операции, используя, например, их представление в виде ДНФ.

Любое из указанных выше равенств можно доказать и непосредственно на языке точек.

6

Пример. Доказать свойство дистрибутивности: А · (В + С) = А · В + А · С. Возьмем любую точку из множества левой части равенства и докажем,

что она принадлежит множеству правой части равенства и наоборот:

a A (B C).

Значит, (А · В + А · С) А · (В + С).

По определению равенства множеств А · В + А · С = А · (В + С).

1.2. Определение и свойства бинарных отношений

1. Определения. Бинарным отношением R из множества А в множество В называется любое подмножество R прямого произведения А × В.

Если А = В, то подмножество множества А × А называется бинарным отношением R на множестве А. Если пара (х, у) принадлежит R: (х, у) R , то говорят, что элемент х находится в отношении R с элементом у, и записывают хRу.

Пример. Множество А есть множество вещественных чисел (множество точек вещественной прямой), тогда А × А – множество точек координатной плоскости. Отношение строгого неравенства < определяется множеством пар R = {(х, у), где x y }. Если на плоскости выбрана декартова

система координат, то отношение < есть множество точек, у которых абсцисса меньше ординаты, т. е. множество точек, лежащих выше биссектрисы 1-го и 3-го координатных углов.

Пример. Введем отношение сравнимости R: х сравнимо с у по модулю m (mod m) тогда и только тогда, когда х и у имеют одинаковые остатки от деления на m (что записывается символом x y (mod m)). Рассмотрим

отношение сравнимости для случая m = 3 на множестве А = {1, 2, 3, 4, 5, 6, 7, 8}, тогда

7

Определение. Областью определения RА бинарного отношения R, заданного на А × В, называется подмножество множества А такое, что RА = {х А & у В: хRу}. Областью значений RВ бинарного отношения R, заданного на А × В, называется подмножество множества В такое,

что RВ = {у В & х А: хRу.

Определение. Множество точек плоскости, координаты (х, у) которых образуют упорядоченные пары некоторого бинарного отношения, называется графиком бинарного отношения.

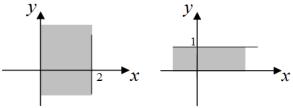
Пример. Графики R1 = {(х, у), где 0 ≤ x ≤ 2} и R2 = {(х, у), где 0 ≤ y ≤ 1} представлены на рис. 1.2.

8

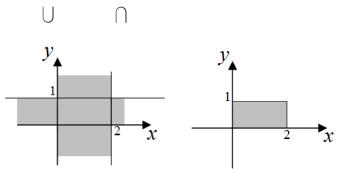
Так как бинарные отношения – это множества, их можно объединять и пересекать. Графики R1 R2 и R1 R2 представлены на рис. 1.3.

Определение. Отношением R 1 , обратным к отношению R, называет-

ся подмножество прямого произведения B × A такое, что R 1 = {(b, а), где

(а, b) R}.

Определение. Пусть R1 A C , R2 C B . Композицией R1◦R2 отно-

шений R1 и R2 называют бинарное отношение из множества А в множество В, определяемое как

R1◦R2= {(а,b),

где ((а А, b В)&( с С): (а,с) R1, (с,b) R2)}, т. е. всякая упорядоченная пара из отношения R1◦R2 образовалась благодаря существованию хотя бы одного элемента с С такого, что он образует упорядоченную пару с элементом а А (второй элемент пары из множества R1), так и с элементом b В (первый элемент пары из множества R2).

Пример: А = {1, 2}, В = {а, b, c}, С = {х, у, z}.

R1 = {(1, х), (1, у), (1, z), (2, х), (2, z)}; R2 = {(х,а),(х,с),(у,b),(z,а)}, тогда

R1◦R2 = {(1, а), (1, с), (1, b), (2, а), (2, с)}.

2. Свойства бинарных отношений

1.Бинарное отношение R на множестве А называется рефлексивным,

если каждый элемент этого множества находится в отношении с самим собой: хRх для х А.

Отношение сравнимости рефлексивно при любом натуральном m и на любом множестве целых чисел.

2.Бинарное отношение R на множестве А называется антирефлексивным, если ни один элемент этого множества не находится в отношении

ссамим собой: х А неверно, что хRх.

9