7. Граничные условия в магнитном поле постоянного тока

Подобно тому, как в электростатическом поле и в поле проводящей среды выполнялись определенные граничные условия, в магнитном поле также имеют место аналогичные условия:

	(43.12)
	(43.13)

Условие (43.12) означает, что на границе раздела двух однородных и изотропных сред, отличающихся значением магнитной проницаемости _, равны тангенциальные составляющие напряженности магнитного поля.

Условие (43.13) свидетельствует о равенстве нормальных составляющих векторов магнитных индукций на границе раздела.

8. Векторный потенциал магнитного поля

Для расчета магнитных полей широко используют величину, которую называют векторным потенциалом (вектор-потенциалом) магнитного поля. Его обозначают . Это векторная величина, плавно изменяющаяся от точки к точке, ротор которой равен вектору магнитной индукции

.

(43.14)

Основанием для представления индукции в виде ротора от вектора-потенциала служит то, что дивиргенция любого ротора тождественно равна нулю.

Известно, что в магнитном поле Подстановка в это равенство вместо дает выражение, тождественно равное нулю: .

Если вектор-потенциал как функция координат известен, то индукцию в любой точке поля определяют путем нахождения ротора от вектор-потенциала. В отличие от скалярного магнитного потенциала, которым можно пользоваться только для областей не занятых током, векторным потенциалом можно пользоваться как для областей, не занятых током, так и для областей, занятых током.

В электротехнических расчетах векторный потенциал применяют для двух целей:

1. определения магнитной индукции;

2. определения магнитного потока, пронизывающего какой-либо контур.

9. Уравнение Пуассона для вектора-потенциала

Воспользуемся законом полного тока в дифференциальной форме и умножим обе части уравнения этого равенства на магнитную проницаемость среды μ_а:

.

Если μ_а постоянна, то ее можно подвести под знак ротора:

(43.15)

В последнее выражение вместо подставим , тогда

	(43.16)
	(43.17)

Так как есть расчетная функция, то в магнитном поле постоянного тока ее можно подчинить требованию . Тогда

(43.18)

Последнее выражение представляет собой уравнение Пуассона. Его общее решение имеет вид:

(43.19)

10. Выражение магнитного потока через циркуляцию

вектор-потенциала

Магнитный поток, пронизывающий какую-либо поверхность S,

Так как , то .

Воспользуемся теоремой Стокса: . Следовательно

(43.20)

Магнитный поток сквозь поверхность S равен циркуляции векторного потенциала вдоль кривой, ограничивающей эту поверхность.

Вопросы для самоконтроля

1. Дайте определение магнитному полю постоянного тока.

2. Какими основными физическими величинами характеризуется магнитное поле?

3. Каков физический смысл векторов 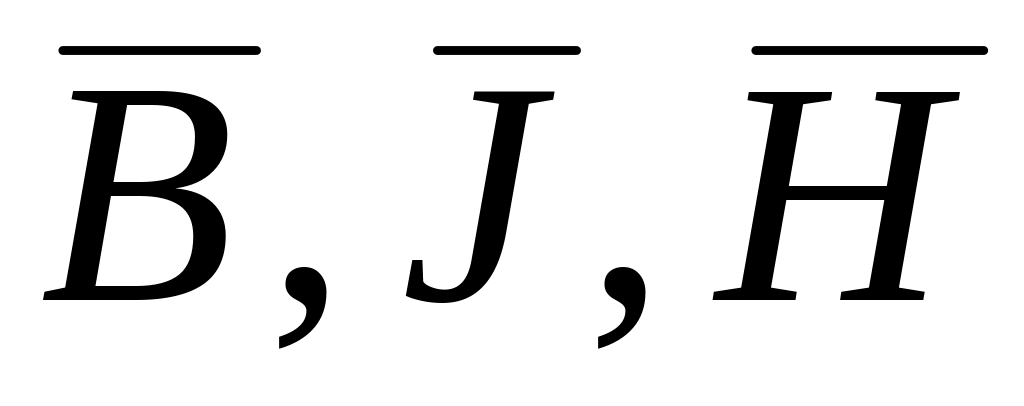и каковы единицы измерения этих величин?

4. Как связаны между собой векторы ?

5. Сформулируйте закон полного тока в интегральной форме.

6. Проделайте вывод закона полного тока в дифференциальной форме?

7. Какие поля называют вихревыми?

8. Дайте физическое толкование понятию ротора.

9. Сформулируйте принцип непрерывности магнитного потока в интегральной и дифференциальной формах.

10. Могут ли линии магнитного поля быть прерывными?

11. К каким областям пространства применимо понятие скалярного магнитного потенциала?

12. Сформулируйте граничные условия в магнитном поле постоянного тока.

13. Какую характеристику называют вектор-потенциалом магнитного поля?

14. Выразите магнитный поток через циркуляцию вектор-потенциала.