Найти общее решение системы линейных уравнений методом Гаусса:
Решение. Сформируем расширенную матрицу:
|
|
|
1-ую строку делим на 3. Получим:
|
|
|
от 2 строки отнимаем 1 строку, умноженную на 2; от 3 строки отнимаем 1 строку, умноженную на 4:
|
|
|
2-ую
строку делим на -
:
|
|
|
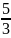к
3 строке добавляем 2 строку, умноженную
на
:
|
|
|
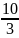3-ую строку делим на -1
|
|
|
Ранг расширенной матрицы = рангу основной матрицы = 4. Следовательно, система совместна. Но так как число переменных меньше ранга, система имеет бесконечное множество решений:
Вычтем
из строки 2 строку 3 умноженную на
.
Получаем:
|
|
|
Вычтем из строки 1 строку 3 умноженную на :
|
|
|
Вычтем
из строки 1 строку 2 умноженную на
:
|
|
|
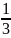Выпишем систему уравнений по последней расширенной матрице:
|
|
x1 |
|
|
|
+ |
|
x3 |
|
|
|
- |
2 |
x5 |
= |
|
3 |
|
|
|
|
|
|
x2 |
+ |
|
x3 |
|
|
|
- |
2 |
x5 |
= |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x4 |
+ |
|
x5 |
= |
- |
1 |
|
x1, x2, x4 оставим в левой части уравнений, а x3, x5 перенесем вправо.
Окончательный вид системы следующий:
|
x1 |
= |
- |
x3 |
+ |
2 |
x5 |
+ |
3 |
|
|
x2 |
= |
- |
x3 |
+ |
2 |
x5 |
+ |
1 |
|
|
x4 |
= |
- |
x5 |
- |
1 |
|
x3, x5 - свободные переменные.
Найти общее решение системы линейных однородных уравнений и записать ее фундаментальную систему решений:
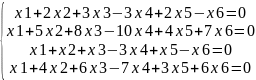
Однородная система уравнений всегда совместна, т.к. ее расширенная и основная матрица совпадают (столбец свободных членов равен нулю), следовательно, она всегда имеет решение. Очевидно, x1 = 0, х2 = 0, х3 = 0, х4 = 0 – решение системы. Такое решение называется тривиальным. Наша задача – найти нетривиальные решения.
Сформируем расширенную матрицу:
|
|
|
Вычтем из строки 2 строку 1, получаем:
|
|
|
Вычтем из строки 3 строку 1:
|
|
|
Вычтем из строки 4 строку 1
|
|
|
Разделим строку 2 на 3:
|
|
|
Вычтем из строки 3 строку 2 умноженную на -1:
|
|
|
Вычтем из строки 4 строку 2 умноженную на 2:
|
|
|
Разделим строку 3 на - :
|
|
|
Вычтем из строки 4 строку 3 умноженную на - . Получим:
|
|
|
Разделим строку 4 на 3:
|
|
|
Вычтем из строки 3 строку 4 умноженную на 7:
|
|
|
Вычтем
из строки 2 строку 4 умноженную на -
:
|
|
|
Вычтем из строки 1 строку 4 умноженную на -3:
|
|
|
Вычтем из строки 2 строку 3 умноженную на . Полученная матрица будет иметь вид:
|
|
|
Вычтем из строки 1 строку 3 умноженную на 3:
|
|
|
Вычтем из строки 1 строку 2 умноженную на 2:
|
|
|
Выпишем систему уравнений по последней расширенной матрице:
|
|
x1 |
|
|
|
|
|
|
|
|
|
+ |
|
x5 |
- |
|
x6 |
= |
|
0 |
|
|||
|
|
|
|
|
x2 |
|
|
|
|
|
|
- |
|
x5 |
+ |
|
x6 |
= |
|
0 |
|
|||
|
|
|
|
|
|
|
|
x3 |
|
|
|
+ |
|
x5 |
- |
|
x6 |
= |
|
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
x4 |
|
|
|
- |
|
x6 |
= |
|
0 |
|