1.1.3. Тестирование моделей

Следует отметить, что процедура применения метода наименьших квадратов при оценивании регрессионной модели позволяет получить состоятельные несмещенные эффективные оценки только в том случае, когда выполнены условия теоремы Гаусса – Маркова, а именно:

1. Математическое ожидание случайной величины εt равно нулю

E(ε1) = E(ε2) = ... = E(εn) = 0,

31

2. Дисперсия случайной величины εt постоянна (случайные возмущения гомоскедастичны)

Var(ε1) = Var(ε2) = ... = Var(εn) = σ ²,

3. Случайные возмущения некоррелированы между собой

Cov(εi, εj) = 0 при любом i ≠ j,

4. Случайные возмущения некоррелированы с объясняющими переменными

Cov(xki, εi) = 0 при всех значениях k=1,…m; i и j.

При этом εt должна быть независимой случайной величиной и иметь нормальный закон распределения.

Подробнее с предпосылками теоремы и ее доказательством можно ознакомиться в книге В.А. Бывшева [2], здесь только отметим, что после получения оценок коэффициентов модели помимо проверки модели, изложенной в пункте 1.1.2, необходимо проверить выполнение условий теоремы Гаусса – Маркова, а также согласие распределения случайных остатков модели нормальному закону распределения вероятности.

Проверка гипотезы о согласии распределения случайных остатков модели нормальному закону.

Напомним, что случайные остатки (возмущения) εt – это разность между эмпирическими уi и теоретическими yˆ _i значениями результативного

32

признака Y. После оценивания модели в примере 1 в Пакете Анализа Регрессия MS Office Excel, значения остатков εt находятся в таблице RESIDUAL OUTPUT столбец Residuals. В таблице 10 представлены случайные возмущения модели примера 1, которые нужно проверить на соответствие нормальному закону распределения (№ п/п соответствует номеру наблюдения, εt – значение случайного возмущения).

Таблица 10.

№ п/п	Residuals (εt)
1	-4,969766015
2	10,47546177
3	-6,982418303
4	3,171943323
5	-3,662784369
6	2,453540319
7	-0,485976725

Для того чтобы проверить согласие эмпирического распределения с известным теоретическим распределением необходимо оценить математическое ожидание и дисперсию по выборке эмпирических данных.

Существуют различные методы получения оценок параметров эмпирического распределения. К ним относятся метод моментов, метод максимума правдоподобия, др. [5]. В работах по статистике показано, что эффективные состоятельные несмещенные оценки параметров для большинства распределений дает метод максимума правдоподобия (ММП).

• случае нормального закона распределения оценки, полученные методом моментов и методом максимума правдоподобия совпадают. Напомним, что плотность вероятности нормально распределенной случайной величины имеет вид

33

1

1

εt − Eεt 

2

pεt  

2π ⋅Varεt 

exp

−

2

⋅

Varεt 

Проверим, что остатки модели в примере 1 имеют нормальный закон распределения.

Для начала оценим математическое ожидание и дисперсию случайных возмущений, воспользовавшись Пакетом MS Excel. Разместим значения остатков εt модели на новом листе в ячейках с A1 по A7. Оценки математического ожидания и дисперсии представлены в таблице 11.

Таблица 11.

E(εt)	=СРЗНАЧ(A1:A7)	0
Var(εt)	=ДИСП(A1:A7)	35,487

Существуют различные методы проверки статистических гипотез.

Наиболее широко используются на практике критерии:

• согласия χ² (хи-квадрат);

• Крамера-Мизеса-Смирнова;

• Колмогорова-Смирнова.

Критерий χ² предпочтителен, если объемы выборок N, в отношении которых проводится анализ, велики. Это мощное средство, если N> 100 значений. Однако при анализе экономических систем иногда бывает довольно трудно (или невозможно) собрать статистику за 100 периодов времени. При относительно малых объемах выборок этот критерий вообще неприменим.

Критерий Крамера-Мизеса-Смирнова дает хорошие результаты при малых объемах выборок (при N < 10). Однако следует отметить, что при N < 10, каким бы методом ни пользоваться, вопрос о доверительной

34

вероятности при проверке статистической гипотезы решается плохо (эта вероятность мала при значительных размерах доверительных интервалов).

• этом случае можно применять метод Монте-Карло для того, чтобы собрать недостающие данные с помощью специального вычислительного статистического инструментария, реализованного на компьютере.

Для реальных объемы выборок, которые можно получить, находящихся в пределах 10 < N < 100 хорошие результаты дает критерий Колмогорова-Смирнова. Он применяется в тех случаях, когда проверяемое распределение непрерывно и известны оценки математического ожидания и дисперсии проверяемой совокупности.

Рассмотрим более подробно алгоритмы проведения проверки согласия эмпирического и теоретического распределений.

Критерий χ².

Проверку можно осуществить, выполняя последовательно следующие

шаги:

1. Разбить эмпирические данные для случайной величины εt на n’ интервалов. Количество интервалов может быть найдено по формуле Стерджесса n’ = 1+3,322lg(n), где n – количество наблюдений.

2. Найти оценки для математического ожидания и дисперсии εt, воспользовавшись формулами для сгруппированных данных

	n′		ε t *
Eε t  	∑ ft
	t1
		n
Varε t  		∑n′	ft ε t * − ε		t 2
		t1				,
			n −1

35

где ft – частота для каждого интервала, εt^* – центральное значение каждого интервала, ε_t – среднее значение, n’ – число групп, n – общее количество наблюдений.

3. Рассчитать значения вероятностей теоретического распределения с параметрами (E(εt) - математическое ожидание и Var(εt) - дисперсия), полученными в предыдущем пункте.

4. Разбить полученные теоретические переменные на пропорциональные интервалы так, чтобы количество наблюдений в каждом интервале было не менее пяти.

5. Определить количество фактических наблюдений, попадающих

• каждый указанный в пункте 4 интервал.

6. Рассчитать критерий проверки

_∑^k N_i − n_i ² _,

i1 N_i

где к – количество интервалов, ni – фактическое количество наблюдений, попавших в интервал i, Ni – количество наблюдений в каждом интервале теоретического распределения.

7. Критическое значение распределения хи-квадрат можно определить, используя встроенные статистические функции MS Office Excel

χ_k²_−r−1 =ХИ2ОБР(α;k-r-1),

где α – заданный уровень значимости, r – количество параметров распределения (в случае нормального распределения r=2)

8. Если неравенство

36

k	N	i	− n	2
∑			i		≤ χk2−r−1
			Ni
i1

верно, то гипотеза H0 о соответствии теоретического и эмпирического распределений принимается.

Критерий w² Крамера-Мизеса-Смирнова.

Порядок проверки гипотезы о согласии эмпирического распределения

• теоретическим осуществляется в соответствии с нижеприведенными пунктами:

1. Вычислить значение статистики S* Крамера-Мизеса-Смирнова по формуле

*

1

n

Fε t −

2t −1

2

S



∑

,

12n

2n

t1

где n – количество наблюдений, F(εt) – значение функции нормального закона распределения в точке εt,

2. Вычислить значение функции распределения a1(S^*) в точке S^*, найденной на предыдущем шаге. Вычисления можно осуществлять по формуле

Γ j  1/ 2

4 j

2

*

1

∞

4 j  1



a1 (S

∑

1

) 

2S

*

Γ1/ 2Γ j  1

exp −

16S

*

,

j0

4 j 

12

4 j  12



I

−1/ 4

− I

1/ 4

*

16S

*

16S

где Г – гамма функция, I1/4 и I-1/4 – модифицированные функции

37

Бесселя.

Найти a1(S^*) можно также, воспользовавшись таблицей 12. Например, при значении S^*=0,01, соответствующее значение a1(S^*)=0,00001, а при S^*=0,69, a1(S^*)=0,98653. Более подробно с таблицей распределения a1(S^*) можно ознакомиться в книге [4].

3. Критические значения критерия Sα,кр. при заданном α могут быть взяты из таблицы 13.

3. Вычислить значение вероятности P{Sα,кр.>S*}=1- a1(S*)

5. Гипотеза H0 о согласии эмпирического и теоретического распределений не отвергается, если для вычисленного по выборке значения статистики S* соответствующая вероятность окажется больше заданного уровня значимости. Т.е. если неравенство P{S>S*}=1-a1(S*)>α выполняется, то гипотеза принимается.

Таблица 12.

S*	0	1	2	3	4	5	6	7	8	9
0,0	0,00000	00001	00300	02568	06685	12372	18602	24844	30815	36386
0,1	0,41513	46196	50457	54329	57846	61042	63951	66600	69019	71229
0,2	0,73253	75109	76814	78383	79829	81163	82396	83536	84593	85573
0,3	0,86483	87329	88115	88848	89531	90167	90762	91317	91836	92321
0,4	0,92775	93201	93599	93972	94323	94651	94960	95249	95521	95777
0,5	0,96017	96242	96455	96655	96843	97020	97186	97343	97491	97630
0,6	0,97762	97886	98002	98112	98216	98314	98406	98493	98575	98653
0,7	0,98726	98795	98861	98922	98981	99036	99088	99137	99183	99227
0,8	0,99268	99308	99345	99380	99413	99444	99474	99502	99528	99553
0,9	0,99577	99599	99621	99641	99660	99678	99695	99711	99726	99740
1,0	0,99754	99764	99776	99787	99799	99812	99820	99828	99837	99847
1,1	0,99856	99862	99869	99876	99883	99890	99895	99900	99905	99910
1,2	0,99916	99919	99923	99927	99931	99935	99938	99941	99944	99947
1,3	0,99950	99953	99955	99957	99959	99962	99964	99965	99967	99969
1,4	0,99971	99972	99973	99975	99976	99978	99978	99979	99980	99980
					38

Таблица 13.

α	0,15	0,1	0,05	0,025	0,01
Sα,кр.	0,2841	0,3473	0,4614	0,5806	0,7434

Поясним приведенный алгоритм проверки гипотеза на примере. Во втором столбце таблицы 14 находятся эмпирические данные εt. Воспользуемся MS Office Excel. Поместим данные в столбец А, строки с первой по десятую. Оценим математическое ожидание E(εt) и дисперсию выборки Var(εt),

E(εt)=СРЗНАЧ(A1:A10)=-0,3165,

Var(εt)=ДИСП(A1:A10)=16,7109

Сформулируем нулевую гипотезу H0: нет существенного различия между распределением случайных остатков εt и нормальным распределением вероятности с математическим ожиданием E(ζ)=-0,3165 и дисперсией Var(ζ)= 16,7109. Для проверки гипотезы воспользуемся критерием Крамера-Мизеса-Смирнова.

Нормально распределенные случайные величины представлены в третьем столбце таблицы 14, их можно рассчитать по формуле Fε_t = НОРМРАСП(εt; -0,3165; 16,7109;1).

Значение статистики Крамера-Мизеса-Смирнова для количества наблюдений n (в нашем случае n=10)

S*=1/120+0,4206=0,4289≅0,43

По таблице 12 найдем соответствующее значение функции распределения a1(0,09)=0,93972. Для заданного уровня значимости, например для α=0,05, критическое значение найдем из таблицы13.

39

Sα,кр.=0,4614.

Таким образом, неравенство Sα,кр.>S* выполняется.

Далее, найдем вероятность P{Sα,кр.>S*}=1-0,43=0,57, P{S>S*}>α. Следовательно, нулевая гипотеза о согласии эмпирического и нормального закона распределения с параметрами математическое ожидание E(ζ)=-0,3165 и дисперсия Var(ζ)= 16,7109 принимается.

Таблица 14.

				2t −1 2
		Fεt 	Fεt −
	ε			2n
t
	t
1	-5,1045	0,1722	0,0149
2	-0,3591	0,1288	0,0004
3	0,3484	0,1954	0,0030
4	-5,9632	0,6899	0,1155
5	-5,8529	0,4818	0,0010
6	4,7184	0,1520	0,1584
7	-4,2995	0,5088	0,0199
8	6,3151	0,9567	0,0427
9	-8,6624	0,8951	0,0020
10	5,6619	0,6999	0,0626
		Σ	0,4206

Критерий Колмогорова-Смирнова.

Проверка согласия двух распределений осуществляется путем задания интегральной функции, следующей из теоретического распределения, и ее сравнения с интегральной функцией распределения эмпирических данных. Сравнение основывается на выборочной группе, в которой

40

экспериментальное распределение имеет наибольшее абсолютное отклонение от теоретического значения. Если эта абсолютная разность меньше критического значения, то статистическая гипотеза о соответствии теоретического распределения эмпирическим данным принимается.

Рассмотрим подробнее методику использования этого критерия на примере проверки соответствия случайных остатков модели объема рынка ИТК (пример1) нормальному закону распределения. В таблице 10 представлены данные (остатки модели), в таблице 11 находятся оценки математического ожидания и дисперсии. Сформулируем нулевую гипотезу H0: нет существенного различия между распределением случайных остатков εt и нормальным распределением вероятности с математическим ожиданием E(εt)=0 и дисперсией Var(εt)=35,487.

Для применения критерия Колмогорова-Смирнова сделаем ряд дополнительных вычислений. Воспользуемся Пакетом Анализа Histogram (Гистограмма) MS Excel для разбиения выборки на интервалы и расчета частоты.

Рис. 2. Вкладка Гистограмма Пакета анализа данных.

41

На рис.2. представлено диалоговое окно данного режима, в котором задан диапазон исходных данных, указана ячейка, начина с которой будут располагаться выходные данные, флажком отмечена необходимость построения графика. Расчеты, автоматически формируемые в MS Excel, представлены в таблице. В первом столбце находятся верхние границы интервалов. Во втором столбце – частота попадания случайного остатка в интервал.

Таблица.

Bin Frequency

-6,9824 1

1,7465 3

10,4755 3

Количество интервалов в Пакете Анализа вычисляется автоматически по формуле Стерджесса. Частота попадания в интервал, деленная на общее число наблюдений, даст нам значение эмпирической вероятности.

Накопленная сумма эмпирических вероятностей распределения находится во втором столбце таблицы. Для нахождения теоретической интегральной вероятности необходимо найти середины интервалов. Их значения находятся в третьем столбце таблицы.

Используя оценки математического ожидания и дисперсии (таблица 11), найдем теоретическую интегральную вероятность. В Excel это легко можно сделать, применяя функцию =НОРМРАСП(εt;E(εt);Var(εt);1), где в качестве εt нужно взять значения из третьего столбца таблицы. Вычисленные значения интегральной вероятности помещены в четвертый столбец таблицы.

Таблица.

Эмпирическая Эмпирическая Середина Теоретическая Абсолютная

42

вероятность	кумулятивная	интервала	интегральная	разность
	вероятность		вероятность	(модуль)
0,1429	0,1429	-11,3469	0,0284	0,1145
0,4286	0,5714	-2,6179	0,3302	0,0984
0,4286	1,0000	6,1110	0,8475	0,4189

Далее найдем абсолютные разности для всех групп значений случайной величины и с помощью столбцов 1 и 4 таблицы 16 получим последний столбец. Нетрудно заметить, что наибольшая абсолютная разность равная D=0,4189 получается в последней группе. В таблице 16 эта разность выделены жирным шрифтом.

Чтобы сделать вывод о согласии распределений, необходимо проверить справедливость неравенства D<Dкр. Для этого найдем критическое значение статистики Колмогорова Dкр. Критические числа в виде, удобном для выполняемой проверки одиночной выборки, приведены в таблице 17. Абсолютную разность 0,4189 необходимо сравнить с критическим значением для заданного уровня значимости.

Таблица 17.

N	D0,10	D0,05	D0,01
1	0,950	0,975	0,995
2	0,776	0,842	0,929
3	0,642	0,708	0,828
4	0,564	0,624	0,733
5	0,510	0,565	0,669
6	0,470	0,521	0,618
7	0,438	0,486	0,577
8	0,411	0,457	0,543
9	0,388	0,432	0,514
10	0,368	0,410	0,490
11	0,352	0,391	0,468
12	0,338	0,375	0,450
13	0,325	0,361	0,433

43

14	0,314						0,349						0,418
15	0,304						0,338						0,404
16	0,295						0,328						0,392
17	0,286						0,318						0,381
18	0,278						0,309						0,371
19	0,272						0,301						0,363
20	0,264						0,294						0,356
25	0,240						0,270						0,320
30	0,220						0,240						0,290
35	0,210						0,230						0,270
	1,22						1,36					1,63
Более 35			N						N						N

При n=7 и значении α = 0,05 критическое значение D0,05=0,486. Поскольку наибольшая разность 0,4189<Dкр, то гипотеза о нормальном распределении остатков модели примера 1 принимается.

Проверка предпосылок теоремы Гаусса Маркова.

Тест Голдфелда – Квандта предназначен для проверки предпосылки теоремы Гаусса–Маркова о гомоскедастичности случайных возмущений, то есть о выполнении равенства

Var(ε1) = Var(ε2) = ... = Var(εn) = σ ²

Для его реализации в ситуации модели линейной множественной регрессии необходимо:

1. исходные данные упорядочить по возрастанию сумм модулей значений регрессоров (x1t, x2t ,…,xmt)

2. разбить упорядоченные данные на два массива таким образом, чтобы количество наблюдений k в первом массиве было на единицу больше количества регрессоров, но меньше половины всех наблюдений (m +1) < k

• n/2, здесь m – количество регрессоров, m+1 – количество оцениваемых коэффициентов функции регрессии.

  3. Оценить уравнение регрессии для каждого массива в отдельности, используя алгоритм, описанный в пункте 1.1.2. В результате получатся две модели с одинаковым уравнением, но различными коэффициентами.

4. Вычислить статистику Голдфелда – Квандта GQ как отношение сумм квадратов отклонений эмпирических данных от теоретических данных для первого массива данных (ESS1) к аналогичной сумме, рассчитанной для второго массива (ESS2)

_{GQ } ^ESS1 _.

ESS₂

Напомним, что число ESS находится в таблице результатов дисперсионного анализа ANOVA Столбец SS, строка Residual (Остаток).

5. Определить критическое значение Fкрит для заданного уровня

надежности α со степенями свободы ν1 и ν2 , при ν1 = ν2 = k – (m+1), где k

– количество наблюдений в первом массиве, m – число регрессоров.

6. Предпосылку о гомоскедастичности случайных возмущений полагать адекватной, если справедливы оба следующие неравенства

GQ ≤ F
	кр		. .
	≤	F
GQ−1
		кр

• противном случае сделать вывод о гетероскедастичности случайных возмущений. Это влечёт потерю свойства несмещённости оценок параметров линейной модели регрессии, полученных методом наименьших квадратов, и неадекватность характеристик точности этих

45

оценок при этом "страдает" только оценка коэффициента a0 модели; оценку коэффициентов ai нарушение не затрагивает. По этой причине не рекомендуется, если нет основания, априори полагать a0 = 0 [см. 2]

При наличии гетероскедастичных случайных возмущений параметры регрессионной модели могут быть оценены при помощи других методов, например, взвешенного метода наименьших квадратов. Этот метод подробно изложен в книге Л.О. Бабешко [1].

Тест Дарбина – Уотсона.

Этот тест предназначен для проверки частного случая третьей предпосылки теоремы Гаусса–Маркова, об отсутствии автокорреляции соседних случайных остатков модели

Cov(εi εj)=0 при j = i-1.

Алгоритм реализации теста:

1. После оценки параметров модели при помощи Пакета Анализа Регрессия значения остатков модели выводятся в столбце Residuals таблицы

2. Используя значения остатков εt, необходимо вычислить статистику Дарбина–Уотсона

n

∑ε_t − ε_t−1 ²

DW 	t2		,
		n
		∑εt2

20. 1

3. По таблице 18 для границ интервала критических значений статистики Дарбина-Уотсона при заданном уровне значимости α определить

46

значения величин dL и dU. В таблице n – количество наблюдений, k – количество объясняющих переменных.

4. На отрезок от нуля до четырех нанести значения DW, dL и dU.

4. Проверить, в какой интервал, обозначенный на рис.3. (M1, M2, M3, M4 или M5) попала величина DW. Сделать вывод, обозначенный на этом рисунке.

Cov(ui ,uj)>0 ←

? →← Cov(ui,uj)=0 →← ?

→← Cov (ui, uj) <0 →

0

dL

dU

24-dU

4-dL

4

←

M1 →← M2 →←

M3

→← M4

→← M5→

Рис.3. Интервалы для проверки отсутствия автокорреляции остатков.

Заметим, что если статистика DW попадает в подмножество M2 = (dL, dU) или M4 = (4-dU, 4-dL), то нельзя сделать вывод о наличие или отсутствии автокорреляции остатков модели и, соответственно об адекватности третьей предпосылки теоремы Гаусса Маркова.

Часто истинной причиной неадекватности предпосылки оказывается ошибка в выборе функции регрессии в спецификации модели, например пропуск значимой предопределённой переменной. Вследствие данного обстоятельства тест Дарбина–Уотсона рассматривается в эконометрике как один из наиболее важных.

Таблица 18.

Границы интервала (dL, dU) критических значений, DWкр , статистики Дарбина–Уотсона (α = 0,05)

	k=1		k=2		k=3		k=4		k=5
n
	dL	dU	dL	dU	dL	dU	dL	dU	dL	dU

47

15	1,08	1,36	0,95	1,54	0,82	1,75	0,69	1,97	0,56	2,21
16	1,10	1,37	0,98	1,54	0,86	1,73	0,74	1,93	0,62	2,15
17	1,13	1,38	1,02	1,54	0,90	1,71	0,78	1,90	0,67	2,10
18	1,16	1,39	1,05	1,53	0,93	1,69	0,82	1,87	0,71	2,06
19	1,18	1,40	1,08	1,53	0,97	1,68	0,86	1,85	0,75	2,02
20	1,20	1,41	1,10	1,54	1,00	1,68	0,90	1,83	0,79	1,99
21	1,22	1,42	1,13	1,54	1,03	1,67	0,93	1,81	0,83	1,96
22	1,24	1,43	1,15	1,54	1,05	1,66	0,96	1,80	0,86	1,94
23	1,26	1,44	1,17	1,54	1,08	1,66	0,99	1,79	0,90	1,92
24	1,27	1,45	1,19	1,55	1,10	1,66	1,01	1,78	0,93	1,90
25	1,29	1,45	1,21	1,55	1,12	1,66	1,04	1,77	0,95	1,89
26	1,30	1,46	1,22	1,55	1,14	1,65	1,06	1,76	0,98	1,88
27	1,32	1,47	1,24	1,56	1,16	1,65	1,08	1,76	1,01	1,86
28	1,33	1,48	1,26	1,56	1,18	1,65	1,10	1,75	1,03	1,85
29	1,34	1,48	1,27	1,56	1,20	1,65	1,12	1,74	1,05	1,84
30	1,35	1,49	1,28	1,57	1,21	1,65	1,14	1,74	1,07	1,83

Отметим так же, что тест Дарбина Уотсона корректен в ситуации, когда случайные возмущения распределены по нормальному закону и гомоскедастичны.

При наличии автокоррелированных случайных возмущений параметры регрессионной модели, полученные методом наименьших квадратов, утрачивают свою объективность. В этом случае для оценки параметров модели может быть использован обобщенный метод наименьших квадратов [1].

48

Case-Study Task 1. Моделирование инфляционных процессов в экономике

Инфляционные процессы занимают важное место в экономической науке, поскольку уровень инфляции и ее социально-экономические последствия играют серьезную роль в оценке экономической безопасности страны и всемирного хозяйства.

Динамика инфляционных процессов в значительной степени определяет восприятие экономической и политической ситуации, складывающейся в стране, российскими и зарубежными экспертными организациями, в том числе международными рейтинговыми агентствами.

• экономической литературе инфляция определяется как процесс длительного и устойчивого обесценивания денег, вызванного снижением их

относительной редкости по сравнению с товарной массой².

Инфляционные процессы являются сложным экономическим явлением и актуальной темой для научных дебатов. Существует множество теорий и моделей, предназначенных для объяснения природы и причин возникновения инфляции. Общеизвестными среди них являются монетаристская модель, модель Филлипса и модель Фридмена.

• данной книге, модель инфляции будет построена на основе

формирования динамической функции совокупного спроса Y_t ^d и динамической функции совокупного предложения Yt ^s , из условия взаимодействия которых можно выразить показатель инфляции π_t и получить динамическую модель для определения уровня инфляции.

2. Макроэкономика. Теория и российская практика / под ред. Грязновой А.Г. – М.: КНОРУС, 2005. – 688 с.

49

∆A_t ),

Преимуществом такого подхода к построению модели инфляции является учет как монетарных (темп прироста денежной массы Mt), так и

немонетарных факторов (изменение автономного спроса воздействующих на уровень инфляции.

Кроме того, модель будет характеризовать развитие инфляционного процесса во времени, при этом будут учтены состояние системы в прошлом и ожидания будущего.

Заметим, что показатель инфляции π_t при таком подходе зависит от

уровня совокупного спроса Y_t ^d и совокупного предложения Y_t ^s , которые в будущий период времени считаются неизвестными. Для их определения дополнительно включим в модель следующие макроэкономические зависимости:

1. Уровень совокупного предложения Y_t s будем моделировать при

помощи уравнения А. Оукена, в котором используется показатель циклической безработицы (U_t − U*) .

2. Уровень совокупного спроса в экономике Y_t d определяется с

помощью моделей агрегированного спроса каждого сектора в открытой экономике:

• для домашних хозяйств – модель совокупного потребления C_t ,

• для предпринимательского сектора – модель спроса на инвестиции

I_t ,

• для государства – модель государственных расходов G_t ,

• для сектора «заграница» – модель объема чистого экспорта NX _t .

• итоге моделируемая система инфляционных процессов будет включать следующие модели:

1. Динамическую модель совокупного спроса.

2. Динамическую модель совокупного предложения на основе

50

уравнения А. Оукена.

3. Модели агрегированного спроса каждого сектора в открытой экономике.

Отметим, что в макроэкономической теории существуют две основные модели агрегированного спроса: кейнсианская и неоклассическая. Различие заключается в выборе наиболее значимого фактора при построении функций спроса. Кейнсианская теория в качестве наиболее значимого фактора рассматривает уровень дохода Y_t , а неоклассическая теория ─ уровень процентной ставки R_t . Показатели Y_t и R_t , а также показатель ε _t обменного курса, содержатся в обеих моделях, поэтому можно

выбрать любую из них. В данном исследовании используется кейнсианская модель агрегированного спроса, которая будет подробно рассмотрена на следующем этапе моделирования.

Динамическая модель совокупного спроса можно вывести из модели IS-LM совместного равновесия на рынках благ, денег и капитала [8]

y ^D P  aA  b ^{M −} ,

P

где A – уровень автономных инвестиций, P – уровень цен, M – уровень денежной массы, M ⁻ ≡ M − P ⋅ c , параметры a  0 , b  0 , c  0 . С повышением уровня цен совокупный спрос снижается, и наоборот.

Инфляция определяется как темп прироста уровня цен в текущем периоде по сравнению с предыдущим P_t − P_{t −1} / P_{t −1} ≡ π _t .

• динамической модели можно учесть наличие инфляционных ожиданий π e . Предположим, что инвесторы ориентируются не на номинальную ставку процента, а на ожидаемое значение реальной ставки

51

процента, т.е. i_r^e  i − π^e . Тогда приращение совокупного спроса будет определяться соотношением, в котором вместо уровня цен P_t появляется зависимость от показателя инфляции

∆Y_t  a∆A_t  bM _t^* − hπ _t  cπ _t^e .

Таким образом, динамическая функция совокупного спроса на рынках благ, денег и капитала Y_t d в текущем периоде зависит от величины спроса в

предыдущем периоде Y_{t −}^d₁ , величины прироста автономных инвестиций ∆A_t , величины M _t^* − π _t , на которую темп роста денежной массы

_{M t}* _ ^M t ^{− M} t−1

^M t−1

превышает инфляцию π_t и корректируется наличием инфляционных ожиданий π_te . В дальнейшем изложении знак звездочка (*) у переменной денежная масса будем опускать ( M _t^* ≡ M _t )

В итоге динамическая функция совокупного спроса имеет вид

Y d

 Y

 a

∆A

 a

M

t

− a

π

t

 a

π e

t

t−1

11

t

12

13

14

t

При этом с ростом автономных инвестиций уровень совокупного спроса возрастает, a₁₁  0 , превышение темпа роста денежной массы над уровнем инфляции обуславливает рост совокупного спроса, a₁₂  0 , инфляционные ожидания также приводят к росту уровня совокупного

52

спроса, a₁₄  0 .

Динамическая модель совокупного предложения может быть построена на основе уравнения А. Оукена, уравнения Филипса и ценообразования по методу «затраты плюс». Рассмотрим процедуру построения модели более подробно.

А. Оукеном была выявлена обратная зависимость между текущим объемом производства Yt и уровнем циклической безработицы.

Уровень циклической безработицы U_t − U *, как было установлено А.

Филипсом, снижается с ростом ставки заработной платы Wt.

	Wt −Wt −1
Темп роста заработной платы		Wt −1	считается пропорциональным

общему росту цен, устанавливаемых по методу «затраты плюс»

P_t  1 λτW_{t .}

Таким образом, инфляция

_{π t } ^Pt ^{− P}t −1 _ ^Wt ^{− W}t −1

^Pt −1 ^Wt −1

вызывает рост объема предложения

s		1		1	 0 .
Yt	 Y * 		π t ,	β
		β

• учетом инфляционных ожиданий π_t^e , увеличивается ставка заработной платы при неизменном уровне объема производства, поэтому

53

динамическая функция совокупного предложения

Y_t ^s  a₂₁  a₂₂ (π _t − π _t^e ) ,

где a₂₁  0 соответствует потенциальному уровню ВВП Y * , рост инфляции вызывает рост объема производства a₂₂  0 .

Уравнение А. Оукена, совокупного предложения, между текущим объемом безработицы,

уже рассмотренное при выводе модели представляет собой обратную зависимость производства Y_t и уровнем циклической

Y_t  a₃₁  a₃₂ ⋅U_t

коэффициент a₃₁  0 соответствует потенциальному уровню ВВП Y*, который корректируется величиной естественной безработицы a₃₂ ⋅U *. При этом рост уровня безработицы снижает объем совокупного предложения

a₃₂  0 .

Общая модель агрегированного спроса каждого из секторов в экономике записывается равенством

Y_t ^d  C_t  I_t  G_t  NX _t

Кейнсианская модель агрегированного спроса состоит из следующих уравнений.

Уровень совокупного спроса домашних хозяйств выражается макроэкономической функцией потребления C_t . Потребление домашних

54

хозяйств возрастает с ростом дохода Y_t

Ct  k11  k12 ⋅Yt ,

k₁₁  0 - соответствует автономному потреблению домашних хозяйств, k₁₂  0 - отражает прямую зависимость между потреблением и уровнем дохода.

Совокупный спрос предпринимателей определяется планируемым объемом инвестиций I_t , который зависит от совокупности прошлых (автономные инвестиции) и ожидаемых (индуцированные инвестиции) обстоятельств.

Ожидаемый объем инвестиций находится в обратной зависимости от ставки процента R_t ,

It  k21  k22 ⋅ Rt ,

k₂₁  0 - соответствует объему автономных инвестиций, k₂₂  0 - отражает обратную зависимость между объемом инвестиций и ставкой процента.

Объем государственных расходов G_t в кейнсианской теории возрастает с ростом уровня Y_t национального дохода

G_t  k₃₁  k₃₂Y_t ,

k31	 0 - некоторый	фиксированный объем расходов государства,
k32  0 -	отражает прямую	зависимость между объемом государственных
расходов и уровнем ВВП.
		55

Спрос сектора «заграница» соответствует величине чистого экспорта NX _t . Возрастает при снижении обменного курса ε _t и при снижении уровня национального дохода Y_t

NX _t  k₄₁  k₄₂ε _t  k₄₃Y_t

k₄₁  0 - некоторый фиксированный объем чистого экспорта, не зависящий от уровня ВВП и от обменного курса, k₄₂  0 - отражает обратную зависимость между объемом чистого экспорта и обменным курсом, k₄₃  0 - отражает обратную зависимость между объемом чистого экспорта и уровнем национального дохода Yt .

Используем рассмотренные выше уравнения для построения итоговой модели инфляционных процессов. При этом сделаем следующие допущения и уточнения.

Допущение 1. Изменение уровня автономного потребления ∆A_t считается некоторой постоянной величиной и поэтому входит в состав коэффициента a₁₁ .

Допущение 2. Величина Y * потенциального объема ВВП и величина u * естественного уровня безработицы являются постоянными, не зависят от периода t, поэтому их можно считать константами и в уравнениях рассматривать их в составе коэффициентов a₂₁ и a₃₁ соответственно.

Допущение 3. Под уровнем денежной массы M _t будем понимать величину агрегата М2.

Модель в виде системы уравнений в структурном виде выглядит следующим образом

56

d

e

ν1

Yt

 Yt −1  a11  a12 M t − a13π t  a14π t

 a

 a

π

− a

π e ν

Y s

21

22

t

22

2

t

t

 a

 a

⋅U

ν

Y s

31

32

t

3

t

d

 Ct  It  Gt  NX t

Yt

Ct  k11  k12 ⋅Yt ν 4

I

t

 k

21

 k

22

⋅ R

t

ν

5

Gt  k31  k32Yt ν 6

NX

t

 k

41

 k

42

ε

t

 k

43

Y

ν

7

t

где ν₁ ,...,ν ₇ - случайные факторы.

Составим схему взаимосвязи переменных в модели инфляционных процессов (Рис.3.). Экзогенные переменные на схеме находятся в серых квадратиках.

Рис.3. Функциональная схема взаимосвязи переменных в модели инфляционных процессов.

• соответствии с полученной схемой перечислим все экзогенные и эндогенные переменные.

К экзогенным переменным модели относятся:

57

Y_t , Y_{t −1} - фактический уровень ВВП в моменты времени t и t-1.

Mt - темп прироста денежной массы (агрегат М2),

R_t - уровень процентной ставки,

ε t - обменный курс	USD	,
	RUR

U_t - уровень безработицы.

Для оценки параметров модели будем использовать квартальные данные, для российской экономики, с 2002 г. по 3 квартал 2008 г., представленные в таблице³.

		Таблица.
	Н		Ф			Уров				Темп		Уро		Об		Урове		Уро
			акт.			ень ВВП в
												вень		менный		нь
	омер							прироста										вень
			уровень			предыдущем
од	кварта							денежной				процентной		курс,		безработицы,		инфляции,
			ВВП,			периоде,
	ла							массы, Mt				ставки, Rt		ε t		Ut		πt
			Yt			Yt-1
	1		2					5,80				5,10		30,		8,47		5,4
002			259,50											91				0
	2		2			2259,		10,9				5,30		31,		7,83		3,4
002			525,70			50		7						32				2
	3		3			2525,		7,36				4,60		31,		7,53		1,1
002			009,20			70								55				9
	4		3			3009,		6,54				4,90		31,		8,70		4,3
002			023,10			20								79				5
	1		2			3023,		9,09				4,43		31,		9,37		5,2
003			850,70			10								38				0
	2		3			2850,		15,5				4,63		30,		8,57		2,5
003			107,80			70		4						35				7
	3		3			3107,		10,2				4,47		30,		8,23		0,6
003			629,80			80		2						61				5
	4		3			3629,		5,17				4,37		29,		8,33		3,1

3. www.cbr.ru ; www.gks.ru

58

003		655,00		80				45			3
	1		3		3655,	17,2	4,30		28,	9,17	3,5
004		516,80		00		9		49			0
	2		3		3516,	5,70	3,70		29,	7,77	2,5
004		969,80		80				03			1
	3		4		3969,	3,66	3,37		29,	7,47	1,7
004		615,20		80				22			9
	4		4		4615,	7,68	3,80		27,	8,23	3,4
004		946,40		20				75			3
	1		4		4946,	9,45	4,33		27,	8,20	5,3
005		459,70		40				83			0
	2		5		4459,	8,74	4,00		28,	7,40	2,5
005		080,40		70				67			6
	3		5		5080,	9,55	3,83		28,	7,17	0,5
005		873,00		40				50			6
	4		6		5873,	5,89	3,80		28,	7,47	2,1
005		212,30		00				78			2
	1		5		6212,	8,93	3,87		27,	7,90	2,8
006		845,30		30				76			0
	2		6		5845,	13,0	4,20		27,	7,47	1,0
006		361,30		30		2		08			7
	3		7		6361,	11,1	4,03		26,	6,63	1,9
006		280,60		30		5		78			2
	4		7		7280,	7,65	4,10		26,	6,73	1,7
006		392,50		60				33			9
	1		6		7392,	11,0	4,97		26,	7,03	1,7
007		747,90		50		9		00			0
	2		7		6747,	20,1	5,17		25,	6,03	1,2
007		749,10		90		1		80			8
	3		8		7749,	4,25	5,13		25,	5,63	3,5
007		826,60		10				00			9
	4		9		8826,	9,04	5,30		24,	5,63	4,0
007		663,70		60				60			3
	1		8		9663,	7,53	5,30		23,	6,73	3,2
008		838,10		70				50			0
	2		1		8838,	4,85	5,37		23,	5,57	3,3
008		0274,7		10				50			9

Эндогенные переменные:

59

π_t - фактический уровень инфляции, для прогнозирования которого

создается модель,

π_te - ожидаемый уровень инфляции, Y_t d - уровень спроса в экономике,

Y_t s - уровень предложения в экономике,

C_t - уровень спроса (конечного потребления) домашних хозяйств, I_t - уровень спроса на инвестиции предпринимательского сектора, G_t - уровень государственных расходов,

NX_t - уровень чистого экспорта.

Переменные Y_t d и Y_t s в основной модели рассматриваются как

эндогенные, которые объясняются с помощью переменных Y_t , Mt, R_t , ε _t , U_t .

Заметим, что эндогенных переменных восемь и модель в структурном виде состоит из 8 уравнений, из которых с помощью преобразований, можно выразить фактический уровень инфляции

π _t  a₀  a₁Y_t  a₂Y_t−1  a₃ M _t  a₄ R_t  a₅U_t  a₆ε _t η_t ,

где η_t - случайный фактор.

Коэффициенты для динамической модели инфляции оценим методом наименьших квадратов. Для этого сформируем обучающую выборку объемом n=24 (данные со второго квартала 2002 г. по 1 квартал 2008 г. таблицы 19). Контролирующая выборка состоит из данных для второго квартала 2008 г. Для оценки параметров модели воспользуемся Пакетом анализа MS Office Регрессия. Результаты представлены в таблице 20.

Таблица.

SUMMARY

60

OUTPUT

Regression

	Statistics
	Multipl	0,73
	e R	009884
	R	0,53
	Square	304431
	Adjust	0,36
	ed R Square	823642
	Stand	1,04
	ard Error	542724
	Obser
	vations	24
	ANOV
	A
										Signifi
		df		SS		MS	F		cance F
	Regre		21,20			3,534	3,234		0,026
	ssion	6	919525		865875		337322		264287
	Resid		18,57			1,092
	ual	17	960809		918123
			39,78
	Total	23	880333
				St			L
		Coe	andard		t	P	ower	pper
		fficients	Error		Stat	-value	95%	95%
	Interce	-	1		-	0	-		2
	pt	3,1770	3,54091		0,23462	,81730	31,7458	5,391
	X	0,00	0,		1,	0	-		0
	Variable 1	08	000802		07065	,29928	0,00083	,0025
	X	-	0,		-	0	-		0
	Variable 2	0,0008	000716		1,16376	,26059	0,00234	,0006
					61

X		-	0,	-	0	-	-
Variable 3	0,1802		066846	2,69617	,01529	0,32126	0,039
X		1,55	0,	3,	0	0	2
Variable 4	24		491458	15879	,00573	,51552	,589
X		-	0,	-	0	-	0
Variable 5	0,4796		354604	1,35264	,19388	1,22780	,2684
X		1,83	0,	2,	0	0	3
Variable 6	445		674693	71894	,01458	,41097	,2579

Коэффициент детерминации модели достаточно невысок R²=0,53. Но при этом он является значимым и регрессоры обладают хорошей объясняющей способностью, поскольку для уровня значимости α = 0,05 критическое значение Fкр=FРАСПОБР(0,05;6;24-(6+1))=2,7≤ 3,234337322, т.е неравенство F≤Fкр не выполняется.

Стандартная ошибка коэффициента a0 превышает значение коэффициента. Кроме того, при α = 0,05 критическое значение tкp =

СТЬЮДРАСПОБР(0,05;24-(6-1))=2,09, следовательно, значимыми коэффициентами, для которых выполняется неравенство |tp| > |tкp|, являются только коэффициенты при третьем, четвертом и шестом регрессоре. Соответствующее P-значение этих коэффициентов меньше заданного уровня надежности α=0,05, т.е. статистики tp являются значимыми и можно сделать вывод, что значимыми являются только регрессоры Mt, Rt, Ut.

Заметим на будущее, что увеличение альфа до, например, α = 0,07 не меняет ситуацию. В этом случае tкp = СТЬЮДРАСПОБР(0,07;24-(6-1))=1,92 и значимыми по-прежнему остаются только регрессоры Mt, Rt, Ut.

Уже на данном этапе можно сделать вывод, что показатель инфляции

практически не объясняется показателем ВВП (факторы Y_t и оказались незначимыми), но хорошо объясняется уровнем процентной ставки R_t . Значит, неоклассическая модель агрегированного спроса точнее подходит для описания инфляционных процессов.

Дальнейшее моделирование инфляции будет производиться для

62

уравнения регрессии вида

π _t  a₀  a₃ M _t  a₄ R_t  a₆ε _t η_t

• этом случае применение Пакета анализа дает следующие результаты

Таблица.

SUMMARY OUTPUT

Regression Statistics

Multiple R	0,60189029
R Square	0,36227192
Adjusted	R
Square	0,26661271

Standard

Error 1,12637554

Observations 24

ANOVA

										Significance
		df	SS		MS	F				F
	Regression	3	14,41436624		4,804788748 3,787109627					0,026639562
	Residual	20	25,37443709		1,268721854
	Total	23	39,78880333
			Standard					Lower		Upper
		Coefficients	Error	t Stat		P-value		95%		95%
	Intercept	-6,592	3,10124	-2,12587		0,0461		-13,061		-0,124
	X Variable 1	-0,120	0,06265	-1,91530		0,0698		-0,2507		0,0106
	X Variable 2	1,2079	0,45681	2,64426		0,0155		0,2550		2,1608
	X Variable 3	0,667	0,25245	2,64563		0,0155		0,1412		1,1945
					63

Стандартные ошибки в этом случае меньше значений коэффициентов. При α = 0,05 критическое значение tкp = СТЬЮДРАСПОБР(0,05;24-(3-1))=2,07. Мы видим, что значение t-статистики для X1 в таблице 21 оказалось меньше критического. Это свидетельствует о незначимости данного регрессора при выбранном значении альфа, и мы должны исключить X1 из модели. Но исключение денежной массы из модели инфляции с точки зрения экономики нежелательно. В этом случае мы можем изменить уровень надежности нашей модели, не потеряв при этом экономического смысла. Так при α=0,07 критическое значение tкp =СТЬЮДРАСПОБР(0,07;24-(3-1)=1,904. Из таблицы 21 видно, что в этом случае все коэффициенты модели, включая свободный член, являются значимыми.

F-тест также дает хороший результат, Fкр =FРАСПОБР(0,07;3;24-(3+1))=2,74<3,787109627, т.е. регрессоры обладают хорошей объясняющей способностью и значение коэффициента детерминации сформировалось не под влиянием случайных факторов. Однако само значение коэффициента регрессии в этом случае оказалось ниже R²=0,36.

Ситуацию можно исправить, если проанализировать зависимость инфляции от времени.

64

Рис.4. Темп инфляции

На рисунке 4 представлена динамика уровня инфляции πt на основе данных таблицы 19. Из рисунка видно, что инфляционный процесс имеет циклический характер. Следовательно, в уравнение для инфляции следует включить циклическую компоненту V_t , которая может быть смоделирована с помощью ряда Фурье для одной гармоники

Vt	 a cost  b sin t ,
где			t		- период времени, a, b - коэффициенты, рассчитанные по
формулам
a 	2				⋅ ∑n	π факт t − π модель t ⋅ cost
			n
					t 0
b 		2			⋅ ∑n	π факт t − π модель t ⋅ sin t
			n
					t 0

Циклическая компонента с оцененными коэффициентами выглядит следующим образом

V_t  - 0,158cost - 0,506sin t

Кроме того, значения коэффициентов можно оценить и в Пакете анализа Регрессия. Результаты оценки представлены в таблице.

Таблица

65

	SUMMARY OUTPUT
	Regression Statistics
	Multiple R	0,732339
	R Square	0,536321
	Adjusted R Square	0,407521
	Standard Error	1,098402
	Observations	24
	ANOVA
						Signifi
		df	SS	MS	F	cance F
					4,16	0,010
	Regression	5	25,11901464	5,023802928	399202	891006
	Residual	18	21,71676897	1,206487165
	Total	23	46,83578361

Из таблицы видно, что включение в модель циклической компоненты повысило коэффициент детерминации, не ухудшив всего остального.

• итоге динамическая модель, которую мы будем применять для прогнозирования инфляции, имеет вид

π _t  −6,59 − 0,12M _t  1,21R_t  0,67U_t − 0,16 cost − 0,51sin t η_t

(2.1.1)

Проверка адекватности модели.

Проверку адекватности модели проведем, используя данные за второй квартал 2008. Для этого вычислим при помощи оценённой модели по значению Mt =4,85, Rt=5,37, Ut =5,57 прогноз величины πt =3,39, значение временного интервала в этом случае равно 25.

π ₂₅  −6,59 − 0,12 ⋅ 4,85  1,21⋅ 5,37  0,67 ⋅ 5,57 − 0,16 cos 25 − 0,51sin 25  2,97

66

Построим доверительные интервалы прогнозной величины с границами

π ₂₅ ⁻  π ₂₅ − t_кр ⋅ S_{π 25} , π ₂₅^  π ₂₅  t_кр ⋅ S_{π 25}

где при α=0,07 для нашей модели критическое значение tкр=1,9. Стандартная ошибка прогноза равна 1,098, а величина среднеквадратичной ошибки прогноза S_{π 25}  0,96 .

Таким образом, доверительные интервалы для прогнозируемой

величины π ₂₅ ⁻  2,97 − 1,9 ⋅ 0,96  1,46, π ₂₅^  2,97  1,9 ⋅ 0,96  4,79 .

Значение за второй квартал 2008 года πt =3,39 попадает в доверительный интервал, следовательно, модель признается адекватной и пригодной для прогнозирования.

Проверка гипотезы о согласии распределения случайных остатков модели нормальному закону.

Математическое ожидание и дисперсия остатков, соответственно равны

13.  E(η_t )  0,0007

σ  σ (η_t )  0,97

Наблюдаемое значение равно 0,028 меньше критического значения

0,461 статистики ω ² . Гипотеза о нормальном распределении случайных возмущений принимается.

Данные,	упорядоченные	по	случ.

67

возрастанию				возмущение
				-1,682
				-0,327
				0,355
математическое		ожидание
случайных возмущений				-0,551
стандартное		отклонение
случайных возмущений				1,037
Статистика	Омега	Квадрат
наблюдаемая				0,028
Статистика	Омега	Квадрат
критическая				0,461
Вывод о принятии гипотезы			принимаем

Тест Дарбина-Уотсона

Значение статистики Дарбина-Уотсона DW=1,77 попадает в третий интервал, следовательно, автокорреляция случайных остатков отсутствует.

Тест Дарбина-Уотсона на наличие автокорреляции случайных возмущений

Статистика DW		1,77
гр	dL	1,12
аницы
	dU	1,66

Cov(ui ,uj)>0		← ?	→← Cov(ui,uj)=0 →← ?						→← Cov (ui, uj) <0 →
0		1,12	1,66			2			2,34		2,88
4
← M1 →←			M2 →← M3				→← M4			→← M5		→

Рис.3. Интервалы для проверки автокорреляции остатков модели.

68

Тест Голдфелда – Квандта

Для его реализации разбьем упорядоченные по сумме модулей регрессоров данные на два массива таким образом, чтобы количество наблюдений в первом массиве k=10 , а во втором массиве n-k=14

Оценим уравнение регрессии для каждого массива в отдельности, и вычислим статистику Голдфелда – Квандта GQ как отношение сумм квадратов отклонений эмпирических данных от теоретических данных для первого массива данных (ESS1) к аналогичной сумме, рассчитанной для второго массива (ESS2)

_{GQ } ^ESS1 _.

ESS₂

• нашем случае число ESS1=3,63, значение ESS2=17,49. Критическое значение Fкрит для заданного уровня надежности α=0,07 со степенями

свободы ν1 и ν2 , при ν1 = ν2 = k – (m+1)=4, где k – количество

наблюдений в первом массиве, m – число регрессоров.

Fкр=FРАСПОБР(α;ν1 ;ν2 )=5,18

Таким образом, справедливы оба следующие неравенства

GQ ≤ F
	кр		.
	≤	F
GQ−1
		кр

Предпосылка о гомоскедастичности случайных возмущений адекватна.

Верификация модели.

69

Судя по оцененным коэффициентам в модели, уровень инфляции обратно пропорционален темпу прироста денежной массы, прямо пропорционален уровню процентной ставки и прямо пропорционален уровню безработицы. Таким образом, все три утверждения в экономической теории подтверждаются.

Наличие циклической компоненты правомерно, поскольку отражает динамику в модели, при этом явно выраженного тренда показатель инфляции не имеет, для него характерны циклические колебания.

Резюмируя вышеизложенное, можно сделать вывод о том, что построенная нами модель динамики инфляционных процессов (2.1.1) может быть использована для прогнозирования уровня инфляции.

Построение прогноза инфляции.

На следующем шаге построим прогноз инфляции на третий квартал 2008 года. Для этого нам необходимо сначала спрогнозировать значения объясняющих переменных. А затем, построив имитационную модель и осуществив направленный вычислительный эксперимент, определить прогнозное значение инфляции.

Рис.5. Динамика уровня безработицы.

70

Проанализировав значения регрессоров в таблице, можно сделать вывод, что для прогнозирования темпа прироста денежной массы и уровня процентной ставки можно использовать вероятностный подход, поскольку значения не содержат временного тренда, а колеблются около некоторого значения. Динамика уровня безработицы изображена на рис.5. Для прогнозирования уровня безработицы необходимо построить модель временного ряда.

Построение вероятностных моделей заключается в подборе теоретических функций распределения для входящих факторов. Функции распределения подбирались из следующих возможных: нормальная, логнормальная, логистическая, экспоненциальная и гамма. Поскольку объем выборки равен 25, то проверка теоретического распределения осуществляется с помощью критерия Колмогорова-Смирнова. При n=25 для уровня значимости α = 0,05 критическое значение D0,05=0,27.

Результаты представлены в таблице.

Таблица.

Характеристика		Вид закона	Наблюдаемое значение
	Обозначение		статистики Колмогорова
показателя		распределения
			Смирнова
темп прироста
денежной		логнормальный,
массы	Mt	α  2,14	D=0,095
ˆ		β  0,41
E(Mt )  9,26
ˆ
σ (Mt )  3,96
уровень		гамма,
процентной	Rt	α=50,55	D=0,112
ставки		β=0,088
		71

E(R_t )  4,44

σ (R_t )  0,39

Как видно из таблицы во всех случаях значение статистики Колмогорова Смирнова, рассчитанное по эмпирическим данным оказалось меньше критического значения, следовательно гипотеза Н0 о согласии эмпирического распределения и известного теоретического принимается для всех входящих переменных.

Самая простейшая модель временного ряда для уровня безработицы может быть построена в Excel путем добавления к динамическому ряду линии тренда. В нашем случае линия тренда может быть аппроксимирована линейной функцией

y=-0,108·t+8,99

Заметим, что коэффициент детерминации в этом случае не очень велик R²=0,64. Ситуацию может исправить включение в модель сезонной компоненты. Из рис.5. видно, что снижение уровня безработицы наблюдается во втором и третьем квартале, в то время, как в четвертом и первом кварталах уровень безработицы растет. Значение квартальной сезонной компоненты можно найти как среднее значение отклонений эмпирических данных для уровня безработицы (см. табл.19) и теоретических значений, полученных по уравнению для линии тренда. В результате модель, позволяющая прогнозировать уровень безработицы будет иметь вид

y=-0,11·t+8,99-ST+ζT,

где ζT – случайная величина, имеющая нормальный закон

72

распределения с параметрами (-0,04;0,5), ST – значения сезонных компонент, представленные в таблице

SI -0,55

SII 0,19

SIII 0,48

SIV -0,03

По результатам проверки адекватности, верификации и валидации, выявлено наличие корреляции модели с входящими факторами и подтверждена целесообразность включения циклической компоненты. Модель устойчива, чувствительна по уровню процентной ставки и уровню безработицы, слабо чувствительна по темпу прироста денежной массы, не содержит лишних входящих факторов, которые предполагались изначально. Модель имеет точность на уровне 88%, не противоречит экономическому смыслу, поэтому пригодна для направленного вычислительного эксперимента.

Величину абсолютной погрешности при прогнозировании каждого регрессора зададим произвольно исходя из экономической сути переменной. Квантиль распределения Стьюдента для уровня значимости α=0,05 и количестве степеней свободы, равном 24, может быть найдена в Excel t=СТЬЮДРАСПОБР(0,05;24)=2,06. В зависимости от величины абсолютной погрешности, найдем соответствующее значение минимальной численности выборки для прогнозирования значений каждого регрессора. Результаты представлены в таблице. Прогнозные значения регрессоров Mt и Rt приводятся с вероятностью 95%, доверительный интервал для переменной Ut: U _{III 2008} ⁻  4,05, U _{III 2008} ^  6,01

Case-Study Task 2. Моделирование цены корпоративной облигации

На фоне разразившегося мирового финансового кризиса,

нестабильной политической обстановки становятся привлекательными консервативные вложения в инструменты долгового рынка. Для сокращения неопределенности относительно их будущей цены можно применять имитационное моделирование.

Наряду с риском изменения структуры процентных ставок на рынке, риска перетекания ликвидности с рынка облигаций на другие рынки, основным из факторов риска облигаций является кредитный риск. Наиболее ярким проявлением кредитного риска является дефолт (default) – неисполнение контрагентом в силу неспособности или нежелания исполнять условий кредитного соглашения или рыночной сделки. В этом случае держатель облигации может потерять часть своих вложений в этот инструмент, получив в соответствии с законом и в порядке очереди лишь часть вложения. Рынок оценивает риск дефолта эмитентов по-разному, анализируя кредитное качество компаний по финансовой отчетности. Свои ожидания относительно вероятности дефолта участники рынка отражают в рыночной цене инструмента.

Прогнозирование цены корпоративных облигаций способствует принятию верных инвестиционных решений, поскольку призвано сократить неопределенность будущего. Позволяет оценить риск негативного изменения цены облигации, тем самым оценивая наихудший возможный исход.

Проанализируем цену корпоративной облигации и проведем ее моделирование на примере облигации Газпром, выпуск 8.

По данной облигации имеется график выплат купонных платежей и номинала, а также значения средних котировок на ММВБ с июня 2007 г. по август 2008 г.

Облигация является купонной, купон фиксирован на уровне 7% годовых, график выплат представлен в таблице.

74

Таблица.

Дата	Ставка		Сумма	Погашение
окончания	купона,	%	купона, RUR	номинала,
купона	годовых			RUR
03.05.2007	7		34,9
01.11.2007	7		34,9
01.05.2008	7		34,9
30.10.2008	7		34,9
30.04.2009	7		34,9
29.10.2009	7		34,9
29.04.2010	7		34,9
28.10.2010	7		34,9
28.04.2011	7		34,9
27.10.2011	7		34,9	1000

Переменные модели.

Модель оценки цены облигации, рассматриваемая в работе, содержит переменные, определяющие рыночный риск (безрисковая ставка) и кредитный риск (интенсивность дефолта). Кроме того, на рыночную цену облигации влияет детерминированная схема выплат по ней. Структура модели представлена на схеме (рис.8).

Поток платежей

Модель цены

Новостной фон

облигации с риском

Цена

(интенсивность

дефолта

дефолта)

Ставка на рынке

Рис.8. Формирование цены облигации в зависимости от входящих

75

факторов

Определение рублевой цены облигации.

Будем проводить анализ на основе цен закрытия. Котировки облигаций приводятся в процентах от номинала, поэтому для получения рублевого значения цены необходимо умножить номинал облигации на котировку в процентах и прибавить начисленный купонный доход (НКД). Если облигация является амортизируемой, то номинал нужно уменьшить на погашенную часть. Таким образом, рублевая котировка облигации может быть выражена формулой

16.  ( F − A) ⋅ Q %  C_ac

где P – рублевая котировка облигации, F – номинал облигации, А – уже погашенная часть номинала, Q% - котировка облигации, например, 99%, Сac – накопленный купонный доход.

Модель цены облигации.

Пусть имеется облигация с номиналом F, по которой выплачивается купоны ci в моменты ti, а затем она погашается в момент tN.

Если облигация безрисковая, то ее чистая приведенная стоимость будет рассчитываться так⁴

N

ci

F

NPV

∑



,

t ⋅r

( t )

t

⋅r

( t

)

i1 e i f

i

e

N

f

N

где r f (t ) –

безрисковая

ставка

на срочность t. Для безрисковой

облигации чистая приведенная стоимость должна совпадать с рыночной ценой.

4. Valuation of risky debt: A Multi-period Bayesian Framework // Leonid V. Philosophov, D. Sc, Professor, Moscow Committee of Bankruptcy Affairs

76

Для корпоративной облигации существует риск дефолта – невыполнения эмитентом обязательства по выплате очередного платежа. Если облигация подвержена риску дефолта, то ее стоимость V представляет собой случайную величину, зависящую от того, в какой купонный период наступил дефолт, и может принимать значения из некоторого множества V₁ , V₂ ,..., V_N , NPV. В таблице ниже представлено распределение случайной величины – стоимости потока платежей держателю облигации.

Таблица.

Временной

Вероятность дефолта во

Значение

дискретной

интервал

временном интервале

случайной величины

t0  t1

D(t1)

V1=0

t1  t2

D(t2)

V2



c1

et1 ⋅rf

( t1 )

…

…

…

tm-1  tm

D(tm)

V



m−1

ci

∑i1

eti ⋅r f ( ti )

m

…

…

…

N −1

ci

tN-1  tN

D(tN)

V

N



∑i1

eti ⋅r f ( ti )

tN  +∞

D(tN+)

V



N

ci



F



N

∑i1 e ti ⋅r f

( ti )

et N ⋅r f ( tN )

Рассмотрим первую строку таблицы. Она отражает ситуацию, когда дефолт происходит в период с t0 до t1, в этом случае держатель облигации ничего не получит.

Если дефолт происходит в период t1  t2, то держатель облигации получает только первый купон, поэтому значение случайной величины V равно дисконтированной стоимости этого купона.

77

Если дефолт происходит в период tm-1  tm, то инвестор получает все купоны вплоть до m-1, затем эмитент отказывается платить по обязательствам. Тогда случайная величина V принимает значение приведенной стоимости потока платежей, включающего купоны вплоть до m-1-го.

Учтем, что владелец облигации в случае дефолта может потребовать возмещения и получит часть номинальной стоимости: RF(ti) (еще не погашенной к моменту ti), тогда случайная величина будет принимать набор значений, представленный в таблице.

Таблица.

Вероятность

Временной

дефолта

во

Значение дискретной случайной

интервал

временном

величины

интервале

t0  t1

D(t1)

V1=0+RF(t0)

t1  t2

D(t2)

V2



c1

 RF (t1)

et1 ⋅rf ( t1 )

…

…

…

tm-1  tm

D(tm)

V



m−1

ci

 RF (t

− )

∑i1

eti ⋅r f ( ti )

m

m 1

…

…

…

N −1

ci

tN-1  tN

D(tN)

V



∑i1

 RF (t

− )

eti ⋅r f ( ti )

N

N 1

tN  +∞

D(tN+)

V



N

ci



F

 RF (t

)



N

∑i1 e ti ⋅r f ( ti )

et N ⋅r f

( tN )

N

Таким образом, случайная величина – стоимость облигации будет иметь математическое ожидание

78

N

E (V )  ∑ D (ti ) ⋅ Vi  D (t N _ ) ⋅VN _ .

1. 1

Вероятности каждого из приведенных сценариев D(ti), заключающихся в том, что дефолт происходит в период с ti-1 до ti, определяются как вероятности дефолта в каждый из интервалов может быть найден по формуле вероятности «дожития»

D (t_i )  S (t_{i −1}) − S (t_i ) ,

где S(ti) – вероятность того, что компания не объявила дефолта вплоть до момента ti. Уровень возмещения RF(ti) определяется как непогашенная часть «по итогам» момента ti. Соответственно, RF (t_N )  0 , поскольку в принятых обозначениях tN – момент погашения облигации.

Для определения вероятностей дефолтов в каждом купонном периоде используются модель, описанная ниже.

Моделирование наступления дефолта.

Вероятность дефолта на протяжении n-го года зависит от вероятности отсутствия дефолта на протяжении n - 1 предыдущих лет. Эта условная вероятность дефолта называется интенсивностью дефолта (default intensity) или уровнем риска (hazard rate). Рассмотрим короткий промежуток времени ∆t. Интенсивность дефолта λ(t ) в момент t определяется так, чтобы величина λ(t )∆t представляла собой вероятность дефолта между моментами

20. и t + ∆t. Пусть S(t) – вероятность того, что компания не объявила дефолта вплоть до момента t. В таком случае

S (t  ∆t ) − S (t )  − λ(t ) ⋅ ∆t ⋅ S (t ) .

Переходя к пределу, получим уравнение

^{dS (t )}  − λ(t ) ⋅ S (t ) .

d (t )

Отсюда следует, что в случае, когда интенсивность дефолта не зависит от времени

t
−∫λ (τ )dτ	 e−λ t .
S (t )  e 0

• результате мы получили формулу для определения вероятности дефолта в момент t

t
−∫λ (τ )dτ			⋅t .
1 − S (t )  1 − e 0	 1− e− λ

Ставка возмещения

Уровень, или ставка, возмещения определяется как часть платежа, возмещаемая в случае дефолта, она связана с уровнем потерь R = 1 - L. Предположения об уровне возмещения достаточно важны и оказывают влияние на модель при расчете интенсивности дефолта λ . В данной работе предположим, что R определяется как доля еще не погашенной части номинала. Оценка нормы возмещения – отдельный вопрос, требующий глубокого изучения отчетности эмитента. Чаще всего⁵ ставку выбирают на уровне 40%. Так поступим и мы. Отметим лишь, что модель от этого не

5. Chad Nunweiler, Philip Watti. Estimating implied corporate default probabilities from bond prices // Simon Fraser University, 2006

80

пострадает, поскольку в любой момент числовое значение R может быть изменено.

Постоянная интенсивность дефолта

Поскольку по мере отдаления момента времени неопределенность финансового состояния эмитента возрастает, то логично предположить, что изменяется и интенсивность дефолта, то есть возрастает λ(t ) от t. Напротив, для компании, находящейся на сегодняшний момент в состоянии кризиса, достаточно пережить начальный момент времени, когда положение стабилизируется. В этом случае временная структура λ(t ) убывает, т.е. для каждого эмитента вопрос о временной зависимости интенсивности дефолта необходимо решать отдельно. Для упрощения понимания экономической сути модели ценообразования облигации, нашей работе будем предполагать, что вероятность дефолта не зависит от времени, т.е.

λ (t )  λ .

• этом случае, как уже отмечалось, формула для вероятности дожития упрощается

S (t )  e^{− λ⋅t}

Отсутствие премии за ликвидность

Будем рассматривать самые ликвидные корпоративные облигации, для которых кредитный спред определяется в основном риском дефолта, а не риском ликвидности.

Поток платежей

• принятых предположениях поток платежей по облигации состоит из купонных выплат и цены погашения облигации в дату оферты (дату

погашения). Для каждой даты оставшиеся платежи известны и

81

представляют собой детерминированную величину при моделировании цены облигации. Поэтому поток платежей в данной модели считается детерминированной составляющей.

Процентная ставка

На приведенную стоимость будущего потока платежей непосредственно влияет безрисковая процентная ставка, превалирующая на рынке. Как правило, это случайная величина, определяемая конъюнктурой рынка.

Для ставки в каждый момент времени соответствует определенная временная структура, ниже изображена самая типичная форма кривой.

Рис.10. G-кривая рынка ГКО-ОФЗ⁶

Считается, что параллельным сдвигом объясняется большинство изменений временной структуры процентных ставок⁷. Будем исследовать

6. http://www.micex.ru/marketdata/indices/state/yieldcurve/chart

7. Frank J Jones. Yield Curve Strategies // The Journal Of Fixed Income, September, 1991. 82

статистические свойства именно этого сдвига.

• качестве безрисковой ставки выберем G-кривую ГКО-ОФЗ, параметры которой публикует ММВБ.

Кривая бескупонной доходности (G-кривая)

Для функционального описания зависимости процентной ставки от срочности на большинстве мировых биржа используется модель Нельсона-Сигеля, в которой фигурирует ряд важных понятий, рассмотрим их подробнее.

Бескупонная доходность – доходность к погашению дисконтной облигации. Кривая бескупонной доходности (zero-coupon yield curve) представляет из себя совокупность бескупонных доходностей для различных сроков до погашения облигаций.

Кривая бескупонной доходности по государственным ценным бумагам (G-кривая) – это график зависимости бескупонной доходности от времени, определенный на основании сделок с облигациями на рынке государственных краткосрочных бескупонных облигаций (ГКО) и облигаций федеральных займов (ОФЗ).

Кривая бескупонной доходности определяется таким образом, чтобы расчетные доходности облигаций оптимальным образом приближали фактические доходности сделок с этими облигациями.

Для описания G-кривой используется параметрическая модель Нельсона-Сигеля с добавлением корректирующих членов (для непрерывно начисляемой процентной ставки)

τ

−

t

−

t

R (t )  β

 ( β  β

)

1 − e τ

− β

e

τ 

,

0

1

2

t

2

−

t 2

−

( t −1) 2

−

( t−2)2

 g e

2

 g

e

2  g

e

2

1

2

3

где первая

строка

–

модель

Нельсона-Сигеля, а вторая –

83

корректирующие добавки для более точного описания начального участка G-кривой.

• рамках данной модели G-кривая однозначно определяется набором из 7 параметров: β ₀ , β₁ , β ₂ ,τ , g₁ , g ₂ , g₃ , которые пересчитываются ежедневно

по базе, состоящей из государственных долговых бумаг. Значения показателей для построения G-кривой на 16.12.2008 приведены в качестве примера в таблице.

Параметры	β0	β1	β2	τ	g1	g2	g3
Среднее за пред. день	970,69	-337,71	149,72	0,73	151,67	-30,3	275,02
На конец пред. дня	973,7	-335,52	150,44	0,65	145,9	-28,91	283,41
Текущее	1 024,51	-320,99	155,37	0,31	140,37	-19,75	323,82

Более подробно с методикой расчета можно познакомиться, например, на сайте http://www.micex.ru/analytics/gko_yieldcurve_4.html.

Интенсивность дефолта

Новостной фон вокруг компании-эмитента и общерыночные ожидания определяют «вмененную» в цену облигации интенсивность дефолта. Будем моделировать ее как случайную величину, распределенную по равномерному закону.

Построение имитационной модели

Изменение временной структуры процентных ставок, как было отмечено выше, связано со сдвигом кривой по вертикали на некоторую величину. Следовательно, для определения текущего положения G-кривой, достаточно смоделировать вертикальный сдвиг уже существующей кривой. Изучим статистические свойства изменения ставки срочностью один год.

Рис.11. Вертикальный сдвиг кривой процентных ставок.

Используя параметры G-кривой можно рассчитать ставки срочностью один год. Значения процентной ставки с июня 2007 по август 2008 года представлены в таблице .

Таблица .

Date	Rate	Date	Rate	Date	Rate	Date	Rate	Date	Rate	Date	Rate
15.06.07	5,35%	24.08.07	5,33%	02.11.07	5,43%	23.01.08	5,38%	04.04.08	5,75%	18.06.08	5,45%
18.06.07	5,34%	27.08.07	5,37%	06.11.07	5,59%	24.01.08	5,26%	07.04.08	5,68%	19.06.08	5,33%
19.06.07	5,36%	28.08.07	5,49%	07.11.07	5,69%	25.01.08	5,15%	08.04.08	5,78%	20.06.08	5,33%
20.06.07	5,33%	29.08.07	5,53%	08.11.07	6,03%	28.01.08	5,19%	09.04.08	5,79%	23.06.08	5,24%
21.06.07	5,37%	30.08.07	5,59%	09.11.07	5,88%	29.01.08	5,24%	10.04.08	5,73%	24.06.08	5,32%
22.06.07	5,34%	31.08.07	5,50%	12.11.07	5,69%	30.01.08	5,24%	11.04.08	5,70%	25.06.08	5,35%
25.06.07	5,31%	03.09.07	5,46%	13.11.07	5,82%	31.01.08	5,32%	14.04.08	5,74%	26.06.08	5,45%
26.06.07	5,35%	04.09.07	5,43%	14.11.07	5,79%	01.02.08	5,32%	15.04.08	5,76%	27.06.08	5,51%
27.06.07	5,30%	05.09.07	5,44%	15.11.07	5,87%	04.02.08	5,43%	16.04.08	5,74%	30.06.08	5,47%
28.06.07	5,23%	06.09.07	5,72%	16.11.07	5,85%	05.02.08	5,52%	17.04.08	5,71%	01.07.08	5,33%
29.06.07	5,24%	07.09.07	5,86%	19.11.07	5,98%	06.02.08	5,45%	18.04.08	5,72%	02.07.08	5,45%
02.07.07	5,25%	10.09.07	5,75%	20.11.07	5,93%	07.02.08	5,54%	21.04.08	5,81%	03.07.08	5,52%
03.07.07	5,30%	11.09.07	5,83%	21.11.07	6,01%	08.02.08	5,62%	22.04.08	5,81%	04.07.08	5,56%
04.07.07	5,26%	12.09.07	5,82%	22.11.07	6,06%	11.02.08	5,71%	23.04.08	5,80%	07.07.08	5,56%
05.07.07	5,20%	13.09.07	5,93%	23.11.07	6,08%	12.02.08	5,67%	24.04.08	5,80%	08.07.08	5,69%
06.07.07	5,25%	14.09.07	5,95%	26.11.07	6,27%	13.02.08	5,66%	25.04.08	5,71%	09.07.08	5,91%
09.07.07	5,17%	17.09.07	5,88%	27.11.07	6,09%	14.02.08	5,74%	28.04.08	5,76%	10.07.08	5,86%
10.07.07	5,21%	18.09.07	6,06%	28.11.07	5,96%	15.02.08	5,80%	29.04.08	5,82%	11.07.08	5,60%
11.07.07	5,17%	19.09.07	6,19%	29.11.07	5,98%	18.02.08	5,80%	30.04.08	5,85%	14.07.08	5,56%

85

12.07.07	5,10%	20.09.07	6,20%	30.11.07	6,11%	19.02.08	5,84%	04.05.08	5,69%	15.07.08	5,63%
13.07.07	5,10%	21.09.07	6,26%	03.12.07	6,11%	20.02.08	5,94%	05.05.08	5,49%	16.07.08	5,57%
16.07.07	5,02%	24.09.07	5,84%	04.12.07	6,13%	21.02.08	5,98%	06.05.08	5,59%	17.07.08	5,57%
17.07.07	5,12%	25.09.07	5,81%	05.12.07	6,00%	22.02.08	5,94%	07.05.08	5,57%	18.07.08	5,56%
18.07.07	5,14%	26.09.07	5,90%	06.12.07	6,00%	26.02.08	5,83%	08.05.08	5,73%	21.07.08	5,64%
19.07.07	5,21%	27.09.07	5,92%	07.12.07	6,06%	27.02.08	5,86%	12.05.08	5,56%	22.07.08	5,63%
20.07.07	5,07%	28.09.07	5,97%	10.12.07	5,98%	28.02.08	6,04%	13.05.08	5,59%	23.07.08	5,74%
23.07.07	5,06%	01.10.07	5,82%	11.12.07	5,91%	29.02.08	6,02%	14.05.08	5,45%	24.07.08	5,65%
24.07.07	5,11%	02.10.07	5,78%	12.12.07	5,91%	03.03.08	5,59%	15.05.08	5,52%	25.07.08	5,43%
25.07.07	5,11%	03.10.07	5,83%	13.12.07	5,78%	04.03.08	5,80%	16.05.08	5,53%	28.07.08	5,46%
26.07.07	5,00%	04.10.07	5,88%	14.12.07	5,79%	05.03.08	5,87%	19.05.08	5,49%	29.07.08	5,61%
27.07.07	5,02%	05.10.07	5,84%	17.12.07	5,86%	06.03.08	5,83%	20.05.08	5,46%	30.07.08	5,60%
30.07.07	4,99%	08.10.07	5,82%	18.12.07	5,91%	07.03.08	5,79%	21.05.08	5,48%	31.07.08	5,55%
31.07.07	5,05%	09.10.07	5,68%	19.12.07	5,82%	11.03.08	5,94%	22.05.08	5,36%	05.08.08	5,64%
01.08.07	4,98%	10.10.07	5,63%	20.12.07	5,72%	12.03.08	5,87%	23.05.08	5,37%	06.08.08	5,59%
02.08.07	5,00%	11.10.07	5,82%	21.12.07	5,72%	13.03.08	5,67%	26.05.08	5,41%	07.08.08	5,70%
03.08.07	4,99%	12.10.07	5,59%	24.12.07	5,76%	14.03.08	5,62%	27.05.08	5,34%	08.08.08	5,72%
06.08.07	4,86%	15.10.07	5,59%	25.12.07	5,66%	17.03.08	5,55%	28.05.08	5,32%	11.08.08	5,83%
07.08.07	4,91%	16.10.07	5,56%	26.12.07	5,62%	18.03.08	5,78%	29.05.08	5,31%	12.08.08	5,86%
08.08.07	4,94%	17.10.07	5,52%	27.12.07	5,83%	19.03.08	5,68%	30.05.08	5,33%	13.08.08	5,83%
09.08.07	5,08%	18.10.07	5,67%	28.12.07	5,57%	20.03.08	5,71%	02.06.08	5,23%	14.08.08	5,77%
10.08.07	4,97%	19.10.07	5,76%	09.01.08	5,78%	21.03.08	5,65%	03.06.08	5,44%	15.08.08	5,71%
13.08.07	4,90%	22.10.07	5,69%	10.01.08	5,74%	24.03.08	5,62%	04.06.08	5,47%	18.08.08	5,80%
14.08.07	5,01%	23.10.07	5,62%	11.01.08	5,46%	25.03.08	5,63%	05.06.08	5,43%	19.08.08	5,85%
15.08.07	4,98%	24.10.07	5,60%	14.01.08	5,36%	26.03.08	5,75%	06.06.08	5,35%	20.08.08	5,80%
16.08.07	5,24%	25.10.07	5,43%	15.01.08	5,32%	27.03.08	5,66%	07.06.08	5,26%	21.08.08	5,99%
17.08.07	5,34%	26.10.07	5,49%	16.01.08	5,37%	28.03.08	5,65%	09.06.08	5,40%	22.08.08	6,00%
20.08.07	5,39%	29.10.07	5,54%	17.01.08	5,26%	31.03.08	5,71%	10.06.08	5,42%	25.08.08	6,16%
21.08.07	5,39%	30.10.07	5,58%	18.01.08	5,19%	01.04.08	5,37%	11.06.08	5,48%	26.08.08	6,16%
22.08.07	5,47%	31.10.07	5,43%	21.01.08	5,20%	02.04.08	5,74%	16.06.08	5,46%	27.08.08	6,12%
23.08.07	5,45%	01.11.07	5,47%	22.01.08	5,31%	03.04.08	5,74%	17.06.08	5,49%	28.08.08	6,00%

Сама по себе ставка процента является случайной величиной, закон распределения которой можно найти, используя статистические данный таблицы. Однако в общепринято моделировать не ставку процента, а величину доходности, которая имеет нормальный закон распределения, а затем от доходности переходить к ставке процента. Используя процентные ставки в таблице, можно рассчитать доходность по формуле

r1year

^yt ^ _r ^t 1year ⁻¹

t−1

Исследуем статистические свойства ряда доходностей. Оценки по методу моментов для математического ожидания  и дисперсии σ² можно получить, используя MS Excel. В этом случае =СРЗНАЧ(B2:B301)=0,03%, σ²=ДИСП(B2:B301)=0,0003.

Сформулируем гипотезу H0: величина доходностей имеет нормальный закон распределения с параметрами (0,0003; 0,016). Для проверки данной гипотезы воспользуемся критерием Пирсона, алгоритм которого реализуем в оболочке MatCalc.

Листинг кода MatCalc для проверки гипотезы о нормальности сдвига кривой.

R=loadvector("shifts2.csv");

m=mean(R); // среднее арифметическое доходностей s=stdev(R); // стандартное отклонений доходностей N=nlaw(m,s); // нормальный закон

• Проводим разбиения, чтобы min(Tf)>5 h=s/4; // шаг разбиения

b=max(R);

while (min(N.intefr(-b:b:h,#R).c(3))<5) b=b-h/2; X=-b:b:h;

Tf=N.intefr(X,#R).c(3); // теоретические частоты Of=R.intfr(X).c(3); // эмпирические частоты assert(min(Tf)>5); // проверка возможности применения критерия

X2 = (Of-Tf)^2 / Tf;

87

x2 = sum(X2);

cr = x2law(#X2-1).invpg(0.05);

pvalue = x2law(#X2-1).pg(x2);

if(x2 < cr) wintitle("Принимается " + pvalue + "; mean=" + m + "; stdev="

+s);

else wintitle("Отвергается " +pvalue);

Y = #R * h * N.den(X);

line(X, Y, black);

hist(R.intfr(X), silver);

axes(h);

Закон распределения эмпирических данных (доходностей) и плотность вероятности нормального закона распределения с параметрами 

• 0,0003; σ = 0,016 представлена на рис.11. p-значение критерия Пирсона при уровне значимости α=0,05 равно 0,08, гипотеза о том, что «доходности» распределены по нормальному закону с параметрами  = 0,0003 и σ = 0,016 принимается.

88

Рис.11. Проверка гипотезы Н0 в программной среде MatCalc.

Итак, временная структура процентной ставки на n периодов вперед будет определяться с помощью добавления к исходной G-кривой случайного сдвига по следующему алгоритму.

1. Пусть на день прогноза имеется некоторая G-кривая: r (τ )  G(τ ) .

2. Определим из нее r₀ – ставку срочностью 1 год

3. Сгенерируем случайную величину

y₁ ~ N (0.0003,0.016)

4. Получим случайную величину ставки на следующий день:

r₁  r₀ (1  y₁)

5. Сгенерируем еще случайную величину: y ₂ ~ N (0.0003,0.016)

5. Получим значение случайной величины ставки через 1 день: r₂  r₁ (1  y₂ )

89

7. И так далее, пока не получим искомое значение процентной ставки. Для прогнозирования на пять дней вперед

r₅  r₀ (1  y₁ ) ⋅ (1  y ₂ ) ⋅ (1  y₃ ) ⋅ (1  y ₄ ) ⋅ (1  y₅ ) ,

где y_i ~ IID - независимые одинаково распределенные по нормальному закону с параметрами N (0.0003,0.016) величины.

Смоделированный сдвиг кривой через пять дней и временная структура процентной ставки определяются формулами

shift  r₅ − r₀

r (τ )  G (τ )  shift

Моделирование интенсивности дефолта

Величина интенсивность дефолта отражает новостной фон вокруг компании-эмитента и влияет на рыночную цену облигации. Как было определено выше, интенсивность дефолта определяет вероятность того, что компания не объявит дефолт к моменту t. Эта вероятность может быть смоделирована по формуле

S (t )  e^−λt

• вероятностью S(t) связано математическое ожидание приведенной стоимости будущих платежей по облигации

N

E (V )  ∑D (t_i ) ⋅ V_i  D (t _{N } ) ⋅V_{N } ,

i1

где вероятность дефолта в период с ti-1 до ti определяется выражением

90

D (t_i )  S (t_{i −1}) − S (t_i )

Оценим по имеющимся котировкам облигации Газпром-8 на ММВБ «вмененные» интенсивности дефолта, т.е. подберем значения интенсивностей λ так, чтобы модельная оценка цены облигации совпадала с реальной рыночной котировкой

^{E (V )  P}model ^{ P}market

Цена облигации Pmodel, рассчитанная по модели, обратно пропорционально зависит от интенсивности дефолта. Значение λ=0 соответствует тому, что величина S(t)=1, т.е. вероятность дефолта равна нулю. В этом случае логично предположить, что модельное значение цены облигации должно быть выше рыночного значения. Таким образом, существует единственное значение λ, уравнивающее модельную и реальную цены. Это значение может быть найдено численными методами. На рисунке 12 представлена зависимость от интенсивности дефолта модельной и реальной рыночной цены облигации. Горизонтальная линия рыночной цены отражает тот факт, что установленная рынком цена уже учла всю негативную и позитивную информацию об эмитенте, и, следовательно, от интенсивности дефолта не зависит.

91

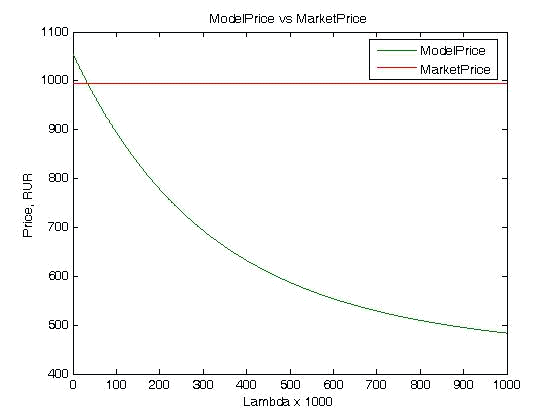
Рис.12. График зависимости цены облигации от параметра λ

Для поиска значений λ при численном решении уравнения

^Pmarket ^{− P}model ^{( λ)  0}

воспользуемся методом половинного деления. Программа для нахождения «вмененной» интенсивности дефолта λ в среде MATLAB представлена ниже.

clc;

• получаем список облигаций bonds = {'gazp8'}; %bonds=bonds';

• обнуляем предыдущие результаты whole_rez=zeros(1);

• получаем параметры G-кривой

92

Curve=csvread('gcurve_averparam.csv');

G_parameters=zeros(1,7);

first_date=min(Curve(:,1));

for p=1:numel(Curve(:,1));

• записываем в массив с индексом: номер дня минус первый имеющийся день

G_parameters(Curve(p,1)-first_date+1,1:7)=Curve(p,2:8); whole_rez(Curve(p,1)-first_date+1,1)=Curve(p,1);

end

• определяем возмещение

• перебираем облигации из списка for jj=1:1

• получаем график выплат

%%file_name=[bonds(i) '.csv'] file_name=strcat(bonds(jj),'.csv') file_name=char(file_name); Grafic=csvread(file_name);

• получаем котировки

file_name=strcat('q',bonds(jj),'.csv')

file_name=char(file_name);

quotes = csvread(file_name);

• количество выплат

N=numel(Grafic(:,1));

• количество имеющихся цен

Nd=numel(quotes(:,1));

• обнуляем лямбды lambdas=zeros(1,2);

• обнуляем счетчик отсутствующих параметров g-кривой

93

no_G=0;

• обнуляем вектор результатов rez=zeros(1,5);

tt=0;

• перебираем дни for q=1:Nd

tt=tt+1; D=quotes(q,1); % дата

if G_parameters(D-first_date+1,1)>0 % если есть параметры кривой на эту дату

MarkPrice=quotes(q,2); % котировка t=(Grafic(1:N,1)-D)/365; % время до выплат, в годах

• ищем выплаты, которые еще не прошли

Npoz=0; for i=1:N if t(i)>0

Npoz=Npoz+1; end

end

c=Grafic(N-Npoz+1:N,3); % вектор оставшихся выплат

F=Grafic(N-Npoz+1:N,2); % вектор непогашенных частей

номинала

tpoz=(Grafic(N-Npoz+1:N,1)-D)/365; % вектор времени до

выплат

r=zeros(Npoz,1); % обнуляем ставки

for i=1:Npoz

r(i)=RfRate(tpoz(i), G_parameters(D-first_date+1, 1:7)); end

cdiscounted=c.*exp(-tpoz.*r);

94

• Перебор значений лямбд f=1;

lam(1)=0;

lam(2)=1;

e=zeros(1);

• Решаем уравнение F=EV-MarkPrice=0 for f=1:2

l=lam(f);

S=zeros(Npoz+1,1); % вектор вероятности дожития DP=zeros(Npoz+1,1); % вектор вероятности дефолтов

RF=zeros(Npoz,1); % вектор возмещений

V=zeros(Npoz+1,1); % вектор PV для купонных периодов

S(1)=1;

• Оценка облигации for i=1:Npoz

S(i+1)=exp(-tpoz(i)*l); DP(i)=S(i)-S(i+1); RF(i)=RR*F(i);

• суммируем элементы потока платежей, полученного к

• моменту дефолта в заданный купонный период

V(i)=RF(i);

if i>1

V(i)=V(i)+sum(cdiscounted(1:i-1));

end

end

DP(Npoz+1)=S(Npoz+1);

V(Npoz+1)=c'*exp(-r.*tpoz); % V(N+1)=NPV

EV=DP'*V;

95

• заполняем вектор результатов:

• [Дата], [MarkPrice], [EV], [Err^2], lambda e(f)=EV-MarkPrice;

end

f=2;

lleft=0;

lright=1;

e=10000000;

e2=e^2;

while e2>0.00001

f=f+1;

lam(f)=(lleft+lright)/2;

l=lam(f);

S=zeros(Npoz+1,1); % вектор вероятности дожития

DP=zeros(Npoz+1,1); % вектор вероятности дефолтов

RF=zeros(Npoz,1); % вектор возмещений

V=zeros(Npoz+1,1); % вектор PV для купонных периодов

S(1)=1;

• Оценка облигации for i=1:Npoz

S(i+1)=exp(-tpoz(i)*l); DP(i)=S(i)-S(i+1); RF(i)=RR*F(i);

• суммируем элементы потока платежей, полученного к

• моменту дефолта в заданный купонный период

V(i)=RF(i); if i>1

V(i)=V(i)+sum(cdiscounted(1:i-1));

96

end

end

DP(Npoz+1)=S(Npoz+1);

V(Npoz+1)=c'*exp(-r.*tpoz);

EV=DP'*V;

• V(N+1)=NPV

• заполняем вектор результатов:

• [Дата], [MarkPrice], [EV], [Err^2], lambda e=EV-MarkPrice;

e2=e^2;

e(f)=e;

if EV<MarkPrice lleft=lleft; lright=l;

else lleft=l; lright=lright;

end

if f>10000

e2

EV

MarkPrice

l

break

end

end

rez(tt,1)= D;

rez(tt,2)= MarkPrice;

rez(tt,3)= EV;

97

rez(tt,4)= (MarkPrice-EV)^2;

rez(tt,5)=l;

else

no_G=no_G+1;

tt=tt-1;

end

end

strcat('report on ',bonds(jj));

no_G

file_name=strcat('results_',bonds(jj),'.csv'); file_name=char(file_name); csvwrite(file_name, rez);

for gg=1:Nd-no_G

if rez(gg,1)>0

whole_rez(rez(gg,1)-first_date+1,jj+1)=rez(gg,5); end

end

end

csvwrite('whole_rez_gazp.csv', whole_rez);

subplot(3, 1, 1);

plot(rez(:,5));

title('Lambdas');

subplot(3, 1, 2);

plot([rez(:,2)]);

title('Market Price');

subplot(3, 1, 3);

plot([rez(:,3)]);

title('Model Price');

98

Расчетные значения интенсивности дефолта, математическое ожидание и стандартное отклонение полученных данных приведены в таблице.

Таблица.

дата	λ	дата	λ	дата	λ	дата	λ
13.06.2007	0,006023	04.10.2007	0,006817	07.02.2008	0,01228	29.05.2008	0,01577
19.06.2007	0,013966	05.10.2007	0,009697	08.02.2008	0,00946	30.05.2008	0,014858
22.06.2007	0,006565	15.10.2007	0,009251	12.02.2008	0,010963	02.06.2008	0,015877
26.06.2007	0,003109	16.10.2007	0,009903	20.02.2008	0,013809	03.06.2008	0,013596
27.06.2007	0,003975	17.10.2007	0,009563	21.02.2008	0,014408	04.06.2008	0,013283
28.06.2007	0,006706	18.10.2007	0,010563	22.02.2008	0,013123	05.06.2008	0,013687
29.06.2007	0,008568	19.10.2007	0,009239	28.02.2008	0,014229	06.06.2008	0,014435
06.07.2007	0,007725	23.10.2007	0,010803	29.02.2008	0,012642	18.06.2008	0,014572
09.07.2007	0,007797	24.10.2007	0,009762	04.03.2008	0,019051	20.06.2008	0,01696
10.07.2007	0,007496	01.11.2007	0,011208	05.03.2008	0,020325	23.06.2008	0,017075
11.07.2007	0,007973	02.11.2007	0,011803	06.03.2008	0,020466	24.06.2008	0,01815
18.07.2007	0,008827	07.11.2007	0,009361	13.03.2008	0,020271	25.06.2008	0,020073
19.07.2007	0,004974	14.11.2007	0,011082	14.03.2008	0,0201	26.06.2008	0,018967
20.07.2007	0,015465	16.11.2007	0,011852	17.03.2008	0,019279	30.06.2008	0,016922
25.07.2007	0,007469	22.11.2007	0,009743	26.03.2008	0,016281	01.07.2008	0,020088
26.07.2007	0,008682	27.11.2007	0,011543	27.03.2008	0,01619	02.07.2008	0,016266
30.07.2007	0,009171	29.11.2007	0,01416	28.03.2008	0,016769	03.07.2008	0,018608
02.08.2007	0,00766	03.12.2007	0,008694	31.03.2008	0,015282	04.07.2008	0,016335
06.08.2007	0,009483	04.12.2007	0,008465	01.04.2008	0,022675	07.07.2008	0,013718
09.08.2007	0,006767	05.12.2007	0,010742	02.04.2008	0,017853	08.07.2008	0,013367
10.08.2007	0,009373	06.12.2007	0,010017	03.04.2008	0,015514	09.07.2008	0,010956
13.08.2007	0,008137	07.12.2007	0,007782	04.04.2008	0,01445	14.07.2008	0,016197
14.08.2007	0,007374	10.12.2007	0,009239	07.04.2008	0,014923	15.07.2008	0,014198
15.08.2007	0,008041	13.12.2007	0,01133	08.04.2008	0,013718	16.07.2008	0,016632
16.08.2007	0,005707	17.12.2007	0,010525	09.04.2008	0,013535	25.07.2008	0,018433
17.08.2007	0,007633	19.12.2007	0,008835	11.04.2008	0,012482	29.07.2008	0,017509
				99

21.08.2007	0,010818	25.12.2007	0,00993	14.04.2008	0,00959	30.07.2008	0,015671
22.08.2007	0,011192	26.12.2007	0,011578	16.04.2008	0,009502	31.07.2008	0,016891
23.08.2007	0,01099	27.12.2007	0,010246	17.04.2008	0,010216	01.08.2008	0,024422
24.08.2007	0,012772	28.12.2007	0,011959	22.04.2008	0,007408	04.08.2008	0,018097
28.08.2007	0,012768	14.01.2008	0,012203	08.05.2008	0,010662	05.08.2008	0,014809
29.08.2007	0,004665	17.01.2008	0,013359	13.05.2008	0,011993	06.08.2008	0,012764
04.09.2007	0,008595	18.01.2008	0,014275	14.05.2008	0,01366	08.08.2008	0,014488
06.09.2007	0,009792	21.01.2008	0,013584	15.05.2008	0,012825	11.08.2008	0,01358
13.09.2007	0,00922	24.01.2008	0,011971	16.05.2008	0,013313	18.08.2008	0,013977
14.09.2007	0,008514	25.01.2008	0,01342	19.05.2008	0,013233	19.08.2008	0,013306
17.09.2007	0,011864	28.01.2008	0,012955	20.05.2008	0,013184	21.08.2008	0,014069
18.09.2007	0,012554	29.01.2008	0,012604	21.05.2008	0,012985	22.08.2008	0,015297
24.09.2007	0,011726	31.01.2008	0,012917	22.05.2008	0,014122	25.08.2008	0,016319
28.09.2007	0,00927	01.02.2008	0,013157	23.05.2008	0,012589	26.08.2008	0,017975
01.10.2007	0,010235	04.02.2008	0,011757	26.05.2008	0,01371	27.08.2008	0,021034
02.10.2007	0,010315	05.02.2008	0,010597	27.05.2008	0,014336	29.08.2008	0,018562
03.10.2007	0,010872	06.02.2008	0,010761	28.05.2008	0,015038	 =0,0132	σ=0,0037

Определим распределение величины интенсивности дефолта. На рис.13. представлен график частот λ, из которого можно предположить, что величина имеет нормальный закон распределения.

Рис.13. Распределение частот интенсивности дефолта.

100

			Накоплен
		Относительная	ная	Теоретич.	Модуль
Интервал	Частота	частота	частота	интег.	отклонения
0,003	1,000	0,005	0,005	0,008	0,003
0,005	1,000	0,005	0,010	0,023	0,013
0,006	6,000	0,029	0,038	0,057	0,018
0,008	11,000	0,052	0,090	0,120	0,030
0,009	19,000	0,090	0,181	0,223	0,042
0,011	52,000	0,248	0,429	0,362	0,067
0,012	30,000	0,143	0,571	0,523	0,049
0,014	32,000	0,152	0,724	0,680	0,044
0,015	20,000	0,095	0,819	0,810	0,009
0,017	14,000	0,067	0,886	0,901	0,015
0,018	9,000	0,043	0,929	0,955	0,027
0,020	6,000	0,029	0,957	0,982	0,025
0,021	7,000	0,033	0,990	0,994	0,004
0,023	1,000	0,005	0,995	0,998	0,003
0,024	1,000	0,005	1,000	1,000	0,000

Сформулирует гипотезу Н0: интенсивность дефолта λ имеет нормальный закон распределения с параметрами (0,0132; 0,0037). Проверка гипотезы при помощи критерия Колмогорова-Смирнова дает следующие результаты, находящиеся в таблице.

Таблица.

При N=171 и значении α = 0,05 критическое значение

D0,05=1,36/N0.5=0,104. Модуль максимального отклонения эмпирических

накопленных частот от интегральной функции нормального закона

101

распределения вероятностей равен 0,067 (выделен в таблице жирным шрифтом), абсолютная разность меньше критического значения статистики Колмогорова, гипотеза H0 принимается. Таким образом, интенсивность дефолта будем моделировать как нормально распределенную случайную с параметрами (0,0132; 0,0037).

Направленный вычислительный эксперимент.

Проведем имитационный эксперимент по определению значений цены облигации через 5 торговых дней. Пусть день проведения эксперимента – 29 августа 2008 года. Тогда оценка будет приходиться на 5 сентября.

Используем имеющийся график оставшихся выплат по Газпром-8 по состоянию на 5 сентября, представленный в таблице .

Таблица.

Дата	Осталось	Сумма	Погашение	Ставки
окончания	дней, ti	купона, RUR	номинала,
купона			RUR
30.10.08	55	34,9		5,2745%
30.04.09	237	34,9		5,7052%
29.10.09	419	34,9		5,9469%
29.04.10	601	34,9		6,2467%
28.10.10	783	34,9		6,6037%
28.04.11	965	34,9		6,8996%
27.10.11	1147	34,9	1000	7,0826%

• этой таблице имеются семь временных периодов до погашения. Для моделирования временной структуры процентной ставки на n периодов воспользуемся приведенным выше алгоритмом. Для этого, используя G-

102

кривую на 29 августа, приведенную на рис.14 и скорректированную модель Нельсона-Сигеля найдем процентные ставки для семи временных периодов, соответствующих дням до погашения, а также ставку срочностью 1 год r0. В нашем случае r0=5,88%.

Рис.14. G-кривая процентных ставок на 29 августа 2008г. По оси OX – года до погашения.

Далее

1. Сгенерируем случайную величину y₁ ~ N (0.0003,0.016) , рассчитаем случайную величину ставки на следующий день r₁  r₀ (1  y₁) и т.д., пока не получим искомое значение процентной ставки на пять дней вперед

r₅  r₀ (1  y₁ ) ⋅ (1  y ₂ ) ⋅ (1  y₃ ) ⋅ (1  y ₄ ) ⋅ (1  y₅ ) ,

где yi – нормально распределенные случайные величины, математическое ожидание и дисперсия которых соответственно равны

0,0003 и 0,016.

i	1	2	3	4	5
yi				-
	-0,0035	0,0173	0,0038	0,0148	0,0155
ri	5,95%	5,92%	5,90%	6,21%	6,88%

2. Найдем величину сдвига G-кривой как разность между r0 и r5. Shift = 0,0688-0,0588=0,01

3. Прибавляя к рассчитанным по модели Нельсона-Сигеля ставкам величину сдвига, найденную на предыдущем шаге, получим значения процентной ставки ri.

r1+shift	r2+shift	r3+shift	r4+shift	r5+shift	r6+shift	r7+shift
5,28%	5,72%	5,96%	6,26%	6,61%	6,91%	7,09%

Используя эти ставки можно построить модельную G-кривую, результаты построения кривой представлены на рис.15.

4. Найдем ожидаемое значение приведенной стоимости будущих платежей по облигации для каждого периода

CFi=ci·exp(-ri· ti /365)+400,

где ri – модельная безрисковая ставка на срочность ti, рассчитанная на шаге 3, ci – величина купона. Значения CF приведены ниже

0	1	2	3	4	5	6	7
400	434,6234	434,6005	434,588	434,5723	434,5541	434,5385	1023,902

104

5. Сгенерируем интенсивность дефолта λ как случайную величину, имеющую нормальный закон распределения с параметрами  =0,0132,

σ=0,0037

5. Рассчитаем значения величины S (t )  e^−λt _{где в качестве t берутся} значения дней до погашения из таблицы, деленные на 365.

i	1	2	3	4	5	6	7
Si	0,997749	0,990338	0,982981	0,975679	0,968431	0,961237	0,954097

7. Найдем вероятность дефолта в период с ti-1 до ti

D (t_i )  S (t_{i −1}) − S (t_i )

i	1	2	3	4	5	6	7
Di	0,002251	0,007412	0,007357	0,007302	0,007248	0,007194	0,0071405

8. Вычислим модельное значение цены облигации

N

E (V )  ∑D (t_i ) ⋅ V_i  D (t _{N } ) ⋅V_{N  ,}

i1

• MS Excel это можно осуществить путем перемножения строки CFi на строку Di В результате расчетное значение цены облигации по данным, представленным на всех предыдущих шагах алгоритма равно 996,77.

105

Рис.15. Временная структура процентной ставки реальная и модельные G-кривые.

Повторяя шаги 1 – 8 N число раз, получим ряд, состоящий из N модельных значений Pmod рыночной цены облигации на 5 сентября. Для N=3500 график частот распределения Pmod представленный на рис.16. является трех модальным. Среди известных теоретических законов распределения функции такого вида отсутствуют.

106

Рис.16. Распределение частот цены облигации.

Определим ожидаемую цену, верхнюю и нижнюю 99% квантили, используя эмпирическое распределение. В результате получена оценка: ожидаемая цена равна 1001,81. С вероятностью 99% она не будет выше 1008,547 и ниже 995,3065.

Построенная имитационная модель для одной облигации – это первый шаг для разработки методики оценки стоимости портфеля таких облигаций. Разработанная модель в этом случае будет генерировать коррелированные оценки стоимостей отдельных облигаций, благодаря тому, что на входе модели они будут иметь один и тот же фактор – определенную временную структуру процентных ставок. Это очень полезное качество такой имитационной модели, поскольку не поднимается вопрос о сложностях моделирования ненормального совместного распределения.

Другим направлением разработки модели может являться учет фактора ликвидности в цене облигации, а также исследование статистических свойств интенсивностей дефолта для того, чтобы предложить некую более точную модель, нежели распределение по нормальному закону.

Case-Study. Task 3.

Description of the Economic system.

In part, economists care about a nation's output (or, more specifically, its Gross Domestic Product) because output is related to employment, and one important measure of a nation's well-being is whether those people who want to work can actually get jobs. Therefore, it's important to understand the relationship between output and the unemployment rate. The (approximate) relationship between output and unemployment is referred to as Okun's Law, after economist Arthur Okun who originally developed the concept in 1962.

When an economy is at its "normal" or long-run level of production (i.e. potential GDP), there is an associated unemployment rate known as the "natural" rate of unemployment. This unemployment consists of frictional and structural unemployment but doesn't have any cyclical unemployment associated with business cycles. Therefore, it makes sense to think about how unemployment deviates from this natural rate when production goes above or below its normal level.

Okun originally stated that the economy experienced a 1 percentage point increase in unemployment for every 3 percentage point decrease GDP from its long-run level. Similarly, a 3 percentage point increase in GDP from its long-run level is associated with a 1 percentage point decrease in unemployment. In order to understand why the relationship between changes in output and changes in unemployment is not one-to-one, it's important to keep in mind that changes in output are also associated with changes in the labor force participation rate, changes in the number of hours worked per person, and changes in labor productivity. Okun estimated, for example, that a 3 percentage point increase in GDP from its long-run level corresponded to a 0.5 percentage point increase in the labor force participation rate, a 0.5 percentage point increase in the hours worked per employee, and a 1 percentage point increase in labor productivity (i.e.

108

β0,1

output per worker per hour), leaving the remaining 1 percentage point to be the change in the unemployment rate.

Since Okun's time, the relationship between changes in output and changes in unemployment has been estimated to be about 2 to 1 rather than the 3 to 1 that Okun originally proposed. (This ratio is also sensitive to both geography and time period.) In addition, economists have noted that the relationship between changes in output and changes in unemployment is not perfect, and Okun's Law should generally be taken as a rule of thumb as opposed to as an absolute governing principle since it is mainly a result found in the data rather than a conclusion derived from a theoretical prediction.

In my creative research work I am going to analyze the relationship between output and unemployment on the example on Spain in the period between 1992-2011. I am going to examine the Okun's law econometrics model with a number of tests in order to understand how growth of output influences the unemoloyment rate in Spain. I will also analyze economic phenomena of the law, evaluate economic relationship between variables and to forecast the behaviour of unemployment rate in Spain in future.

Formulation of the problem.

Mathematical form.

Here is a mathematical representation of the Okun’s law. General form of the fitted line:

Yi = β0 + β1Xi,

Where Yt – is the change in the unemployment rate in percentage points, Xi – is the percentage growth rate in real output, as measured by real GDP, – parameters (sensitivity of the explained variable to changes of the

explainable variable).

Econometric initial form.

Ut = β (Ygt – Yt) + Ut-1 + εt

β > 0

t = 1, 2, 3…

Where Ut – is the unemployment rate in year t,

Ut-1 – is the unemployment rate in the previous year,

Yt – is the output growth rate from previous year,

Ygt – is the output growth rate,

• – is a coefficient,

εt – is the disturbance term.

Determination of the variables.

Endogenious variable.

Yt – annual GDP growth (in percentages).

Gross domestic product (GDP) represents the sum of value added by all its producers. Value added is the value of the gross output of producers less the value of intermediate goods and services consumed in production, before accounting for consumption of fixed capital in production. The United Nations System of National Accounts calls for value added to be valued at either basic prices (excluding net taxes on products) or producer prices (including net taxes on products paid by producers but excluding sales or value added taxes). Both valuations exclude transport charges that are invoiced separately by producers.

Annual percentage growth rate of GDP at market prices based on constant local currency. Aggregates are based on constant 2005 U.S. dollars. GDP is the sum of gross value added by all resident producers in the economy plus any product taxes and minus any subsidies not included in the value of the products. It is calculated without making deductions for depreciation of fabricated assets or for depletion and degradation of natural resources.

Exogenious variables.

Un – total unemployment, out of total labour force (in percentages).

Unt-1 – previous yeat total unemployment, out of total labour force (in percentages).

110

Unemployment refers to the share of the labor force that is without work but available for and seeking employment. Definitions of labor force and unemployment differ by country.

Description of statistical data related to te the model.

In order to analyze and test the Okun’s law, we should find out some specific data for the variables We’ve listed above: a percentage change in GDP, and the unemployment rate.

As the source for my data I used http://data.worldbank.org, whwe ch is a reliable source of information. The World Bank is a vital source of financial and technical assistance to developing countries around the world and it, fortunately, has free and open access to data about development in countries around the globe.

The country I have chosen for my investigation is Spain. It is a country with total population of 46.22 million people and with a GDP of $1.349 trillion (in current US$).

WE have taken quarterly data from the 1992 to 2011.

Also it’s important to mention, that the last interval of 2011 shouldn’t be involved in our analyzing, but we will need it later for model forecasting.

				Unempl
	GDP	Unemploy	oyment, previous
	growth	ment, total (% of	year	total (% of
	(annual %)	total labour force)	total	labour
			force)
	Y	Un		Unt-1
1992	0,93	18,10		16,10
1993	-1,03	22,40		18,10
1994	2,38	23,90		22,40
1995	2,76	22,70		23,90
1996	2,42	22		22,70
1997	3,87	20,60		22
1998	4,47	18,60		20,60
1999	4,75	15,60		18,60
2000	5,05	13,90		15,60
2001	3,67	10,5		13,90
2002	2,71	11,40		10,5
2003	3,09	11,30		11,40
2004	3,26	11		11,30
2005	3,58	9,20		11
2006	4,08	8,5		9,20
2007	3,48	8,30		8,5
2008	0,89	11,30		8,30

111

2009	-3,74	18	11,30
2010	-0,32	20,10	18
2011	0,42	21,60	20,10

Model specification.

Calculation of the correlation matrix.

First of all, it is necessary to check the relationship between endogenous and exogenous variables as well as to find out whether there is multicollinearity among exogenous variables. In order to do this WE constructed a matrix of pair correlations for my variables.

	Y	Un	Unt-1
Y	1
Un	-0,39	1
Unt-1	0,04	0,89	1

Let’s consider the relationship between the regressors and the regressand. r1 equals to -0.39, a weak negative value, which implies that there is no

relationship between Y and Un.

r2 equals to 0.89, a value close to 1, which means that there is a strong positive linear relationship between Un and Unt-1.

r3 equals to 0.04, a weak positive value, it indicates that there is no linear relationship between Y and Unt-1.

Scatter diagram.

The dependence of the particular exogenous variable with our endogenous variable can be shown using scatter diagrams. Analysis of linear trends and coefficients of determination for each scatter diagram revealed the following results.

112

The diagram shows that there is a linear dependency of two variables: Un and Y. Since the slope is downward sloping, there is a negative relationship. So, the correlation analysis and the scatter diagram have shown that there is no strong dependency of change in unemployment rate and potential GDP growth rate. With the change in one variable, another one does not change with the same rate.

Regression analysis.

Now we come to the estimation of the econometrics model. The first step is linear regression analysis, which can be conducted with the use of the function (=LINEST(range;constant;statistics)). We choose the range of our values, put 1 as a constant, as we have an a0 coefficient and put 1 for statistics. Doing so, we obtain the information about our coefficients and their estimations, standard deviation, R² and F values.

a2	a1	a0
0,78	-0,83	3,32
0,08	0,08	0,61
0,88	0,82	#Н/Д
57,52	16	#Н/Д
77,89	10,83	#Н/Д

113

The second step of model estimation is regression analysis. It is conducted with the help of “data analysis” tool. Regression analysis enables us to take a broader look at the estimation of coefficient, gives us the value of the disturbance term and provides us with the information needed for further tests. So, WE received these figures:

	Regression Statistics
	Multiple R					0,94
	R Square					0,88
	Adjusted R Square					0,86
	Standard Error					0,82
	Observations					19
				df	SS	MS	F		Significance F
			Regression	2	77,89	38,95	57,52		0,000000049
			Residual	16	10,83	0,68
			Total	18	88,73

						Lower	Upper	Lower	Upper
		Coefficients	Standard Error	t Stat	P-value	95%	95%	95,0%	95,0%
	Intercept	3,32	0,61	5,42	0,000057	2,02	4,62	2,02	4,62
	Un	-0,83	0,08	-10,68	0,000000011	-0,99	-0,66	-0,99	-0,66
	Unt-1	0,78	0,08	9,89	0,000000032	0,61	0,95	0,61	0,95

Using the information, obtained from the regression analysis, we can transform our initial econometric model into an estimated form:

Yt = 3.32 – 0.83 X1t + 0.78 X2t + εt

(0.61) (0.08) (0.08) (0.82)

R² = 0.88

F = 57.52

It includes all the variables needed: Yt -unemployment rate, X1,2t – Unt and Unt-1. Where a0 = 3.32 with standard error of 0.61, a1 = (-0.83) with standard

114

error of 0.08, a2 = 0.78 with standard error of 0.08; the standard error of disturbance term is 0.82.

Model testing.

The next step is model testing, which purpose is to check the model’s adequacy and its appropriateness for future forecasting.

R²-test.

If R² is close to 1, out regression model explains the values of Y with the given X values. In my case, the value of R² is 0.88, which shows that 88% of total deviation of Yi is explained by the variation of the factors xi. That means that selected external factors significantly affect unemployment, which confirms the correctness of their inclusion in the estimated model.

F-test.

F-test is conducted in order to check the correctness of the R² value and the quality of the specification of the model. We must use data analysis to assess the needed variables. If Fcrit is lower that F, than the quality of specification of our model is high. In order to find Fcrit, we use the function (=F.INV.RT(probability of mistake;degree of freedom_regression;degreeof freedom_residual)). Probability of mistake is 0.05, the number of regressors is 2, the number of residuals is 16, so I obtained such results:

Fcrit 3,63

F 57,52

It is clearly seen that Fcrit < F, so we can conclude that the quality of the model’s specification is high and the value of R² is correct.

T-test.

The student’s t-test checks the significance of coefficients. We test the inequality |t|≥tcrit, where t is the value of t-statistics. If the inequality is right, the

115

coefficient and its factor variable are considered to be significant. The formula for

calculation of t- values of t is .

We have these figures in our linear regression analysis.

	a2	a1	a0
	0,78	-0,83	3,32
	0,08	0,08	0,61
	0,88	0,82	#Н/Д
	57,52	16	#Н/Д
	77,89	10,83	#Н/Д
t	9,89	-10,68	5,42	t1 > tcrit	-> coefficient is significant
tcrit					-> coefficient is not significant and must be
	2,12			t2 < tcrit	excluded
				t3 > tcrit	-> coefficient is significant

The function that we use for finding Tcrit is =(T.INV.2T(probability of mistake;degrees of freedom)). For the probability of mistake we usually take not more that 0.05. To calculate degrees of freedom, we use the formula: df = n – k, where n is № of observations, k is № of estimated parameters and can be obtained by: k = 1 + m, where m is № of regressors. All these figures are in our regression analysis. In my case, k = 1 + 2 = 3, so df = 19 – 3 = 16.

So, WE have checked three t –values and obtained that t1,3 = 9.89 and 5.42, both more that tcrit, which means that coefficients are significant and we can use them; t2= -10,68, which is less than tcrit, so the coefficient is not significant and must be excluded from the model.

Goldfield-Quandt test.

Goldfield-Quandt test is designed to check the second assumption of Gauss-Markov theorem about homoscedasticity of random disturbances, i.e. about the following equality satisfying: Var(ɛ1) = Var(ɛ2) =…=Var(ɛn)=σ².

We must find the coefficients GQ and , and compare them with Fcrit, they have to less the critical value of F. GQ is equal to RSS1/RSS2. (RSS – Residual Sum of Squares). First, we must take our table with initial data and take the

116

absolute values of the X variable, using the formula (=ABS). Now we must sort the table by these absolute values into ascending order. Then we must divide our table into two separate subsamples. Using data analysis for the two subsamples, we must find the values of the residual sum of squares for both samples.

The result is as follows:

					Sum of abs
		Y	Un	Unt-1	(X)
	2007	3,48	8,30	8,5	16,80
	2006	4,08	8,5	9,20	17,70
	2008	0,89	11,30	8,30	19,60
	2005	3,58	9,20	11	20,20
	2002	2,71	11,40	10,5	21,90
	2004	3,26	11	11,30	22,30
	2003	3,09	11,30	11,40	22,70
	2001	3,67	10,5	13,90	24,40
	2009	-3,74	18	11,30	29,30
	2000	5,05	13,90	15,60	29,50
	1992	0,93	18,10	16,10	34,20
	1999	4,75	15,60	18,60	34,20
	2010	-0,32	20,10	18	38,10
	1998	4,47	18,60	20,60	39,20
	1993	-1,03	22,40	18,10	40,50
	2011	0,42	21,60	20,10	41,70
	1997	3,87	20,60	22	42,60
	1996	2,42	22	22,70	44,70
	1994	2,38	23,90	22,40	46,30
	1995	2,76	22,70	23,90	46,60

	df	SS		df	SS
Regression	2,00	48,25	Regression	2,00	32,23
Residual	7,00	6,68	Residual	7,00	3,97

RSS1	6,68
RSS2	3,97
Fcrit GQ	4,74

GQ	1,68
1/GQ	0,59
GQ	<	FcritGQ
1/GQ	<	FcritGQ

117

Fcrit GQ is calculated with the formula (=F.INV.RT(probability of

mistake;residual;residual)). GQ is equal RSS1/RSS2.

So, it is clear from my calculations, that GQ and are less than Fcrit GQ.

This means that residuals are homoscedastic, the second Gaus-Markov theorem is confirmed and we may use the OLS (ordinary least squares) in order to estimate model coefficients.

Durbin-Watson test.

This test is used to confirm the third Gauss-Markov condition. The critical values for the Durbin-Watson test are the following:

1. T – number of observations

2. K – number of estimated parameters

3. dl – lower level of D-W statistics

4. du – upper level of D-W statistics

In order to obtain dl and du, we use the external source: http://www.stanford.edu/~clint/bench/dwcrit.htm. We use 5% significance level, the number of my observations is 19, the number of estimated parameters is 3.

So WE have:

T

19

K

3

dL

1.07430

dU

1.53553

Now

we

must

find

the

DW

statistic,

which

is

equal

to

^{difference sum of squares} . To find these numbers, we must make conduct several

residual sum of squares

calculations:

Residuals
0,00065
0,03	0,00065	0,03	0,00089	0,00093
1,33	0,03	1,30	1,69	1,77
-0,45	1,33	-1,79	3,19	0,21
-0,44	-0,45	0,02	0,00029	0,19
0,41	-0,44	0,84	0,71	0,16
				118

0,44	0,41		0,04		0,0016	0,20
-0,19	0,44		-0,64		0,41	0,04
1,04	-0,19		1,24		1,53	1,09
-1,82	1,04		-2,86		8,19	3,30
0,62	-1,82		2,43		5,92	0,38
0,21	0,62		-0,40		0,16	0,04
0,21	0,21		0,00		0,000000029	0,04
-0,72	0,21		-0,93		0,86	0,51
0,60	-0,72		1,32		1,74	0,36
0,39	0,60		-0,22		0,05	0,15
0,43	0,39		0,04		0,0020	0,18
-1,01	0,43		-1,44		2,09	1,03
-1,08	-1,01		-0,06		0,0041	1,16
				Sum	26,55	10,83

So, the DW is 26.55/10,83 = 2.45

DW 2,45

Now we have to check whether our model is adequate or not.

For doing this, we make a table with 4 intervals:

1. 0 to dl

2. 4-dl to 4

3. dl to du and 4-du to 4-dl

4. du to 4-du

Then, we check in which interval does the DW constant goes to. The law states that if DW constant is between 0 and dl, there is positive autocorrelation in residuals, if it is between 4-dl and 4, there is negative autocorrelation in residuals. In both cases we cannot use OLS in order to estimate the coefficients. If DW lays between dl and du, or between 4-du and 4-dl, there is no information about autocorrelation. If DW is between du and 4-du, there is no autocorrelation in residuals, the third Gauss-Markov condition is confirmed and we may use OLS for estimating the coefficients.

0	dl	du	2		4-du	4-dl	4
							4
0	1,07	1,54	2		2,46	2,93	4
				119

My DW constant is 2.45, so, in my case, it lays in the yellow interval between du and 4-du, which indicates that there is no autocorrelation in residuals, the third Gauss-Markov condition is confirmed and we may use OLS for estimating our model.

Confidence level.

The last step of our model-testing is checking confidence intervals in order to make sure that our model is adequate.

We have to make sure that the real value of Yt lies between the lower and the upper boundaries of Y. That is where we finally use the last interval of 2011.

1. First, we find the real value of Yt: (=a0 + a1 * x1t + a2 * x2t).

2. Then, we calculate the boundaries:

Yt^- equals (=RealYt – tcrit * standard error)

Yt⁺ equals (=RealYt + tcrit * standard error)

WE have obtained:

Real Yt

1,16

Yt^- -0,59

Yt⁺ 2,90

It follows that the real value of Yt in 2011 belongs to the confidence interval, so the model is adequate and may be used for forecasting.

Forecasting.

Finally, we are calculating the percentage deviation of the forecast from the real value, with intention to find out whether this forecast is good.

120

[|Yt-Yreal|/Yreal]*100% =

The deviation of the forecast from the real value is fairly small, thus, this forecast may be considered as a good one, and the high quality of the model for making forecasts is confirmed once again.

Conclusion.

To sum up, I’ve analyzed the relationship between output and unemployment on the example on Spain in the period between 1992-2011. After examination of the econometric model and passing a number of tests, WE came to a conclusion that Okun's law is applicaple in chosen conditions and may be useful to economists and policy-makers in making assessments of the future unemployment rate in Spain.

References.

1. Трегуб, И.В.Математические модели динамики экономических систем: монография — М. : Финакадемия, 2009 .— 118 с.

   2. http://data.worldbank.org

2. http://www.stanford.edu/~clint/bench/dwcrit.htm

2. http://economics.about.com/od/unemployment-category/a/Okuns-

Law.htm

2. Карлова. Relationship between Output and Unemployment in Spain

121

ЛИТЕРАТУРА

1. Бабешко Л.О. Основы эконометрического моделирования. – М.:

КонКнига, 2006. 432с.

2. Бывшев В.А. Эконометрика. М.: Финансы и статистика, 2008. 480с.

3. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики.

– М.: Наука, 1983. – 416с.

4. Клейнен Дж. Статистические методы в имитационном моделировании / Пер с англ.; Под ред. Ю.П.Адлера и В.Н.Варыгина. – М.: Статистика, 1978. – Вып.1 – 221с.; Bып.2 – 335с.

5. Макроэкономика. Теория и российская практика / под ред. Грязновой А.Г. – М.: КНОРУС, 2005. – 688с.

5. Трегуб И.В. Имитационное моделирование: Учебное пособие. – М.: Финакадемия, 2007. – 145с.

122