1.3 Погрешности измерений и их классификация

Результат измерения всегда отличается от истинного значения измеряемой физической величины, то есть находится с некоторой погрешностью.

Источниками погрешности являются.

• несовершенство применяемых методов, средств измерений;

• внешние и внутренние помехи;

• климатические условия;

• порог чувствительности измерительных приборов;

• индивидуальные особенности экспериментатора.

Рассмотрим некоторые признаки, по которым классифицируются погрешности измерения.

1) По способу количественного выражения погрешности делятся на абсолютные, относительные, приведенные.

• абсолютной погрешностью , выражаемой в единицах измеряемой величины, называют отклонение результата измерения х от истинного значения х_и.

(1.5)

• для сравнения качества (точности) измерений вводится понятие относительной погрешности.

Относительная погрешность  – отношение абсолютной погрешности измерения к истинному значению измеряемой величины.

(1.6)

Для сравнения различных приборов используют понятие приведенной погрешности.

Приведенная погрешность _пр, выражающая потенциальную точность измерений, – это отношение абсолютной погрешности  к некоторому нормирующему значению X_N (например, к конечному значению шкалы прибора).

(1.7)

2) По характеру (закономерности) измерения погрешности подразделяются на систематические, случайные, грубые (промахи).

Систематические погрешности _с – составляющие погрешности измерений, остающиеся постоянными или закономерно изменяющиеся при многократных измерениях одной и той же величины в одних и тех же условиях.

Случайные погрешности ⁰ – составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины в одних и тех же условиях.

Грубые погрешности – погрешности, существенно превышающие ожидаемые при данных условиях измерения.

Без учета промахов, абсолютная погрешность измерения –  определяется как сумма систематической и случайной погрешностей и как сумма является случайной величиной.

(1.8)

1.4 Прямые измерения и их классификация

При наличии значительных случайных погрешностей существует необходимость многократных измерений случайной величины х_и.

В соответствии с ГОСТ 8.207-76:

1. Для оценки результата измерения считается, чтобы при выполнении n многократных наблюдений одной и той же величины x_и постоянная систематическая погрешность _с полностью исключена.

2. Тогда результат некоторого i^го наблюдения находится с некоторой абсолютной случайной погрешностью

(1.9)

3. За истинную величину х_и=А принимают ее оптимальную оценку х^=А^ в виде среднеарифметического значения ряда наблюдений:

(1.10)

зная оценку х^- истинного значения величины х_и, вычисляют абсолютную погрешность каждого из n наблюдений:

(1.11)

4. Затем находят оценку среднеквадратического отклонения ^- наблюдений, характеризующую точность метода измерений:

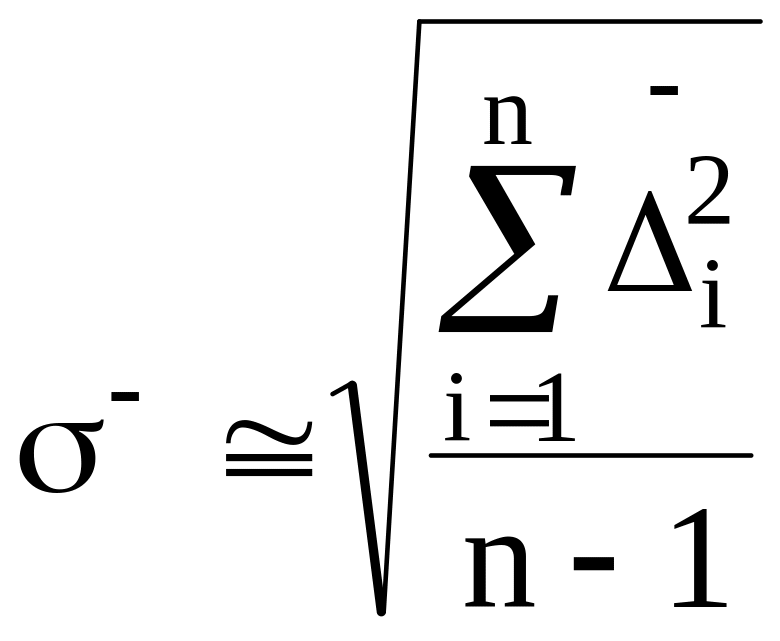(1.12)

5. Оценка измеренного истинного значения зависит от числа наблюдений n и является случайной величиной. Поэтому вводят для х^- оценку – среднеквадратическое отклонение результата измерений , которое характеризует степень разброса значений по отношению к истинному значению:

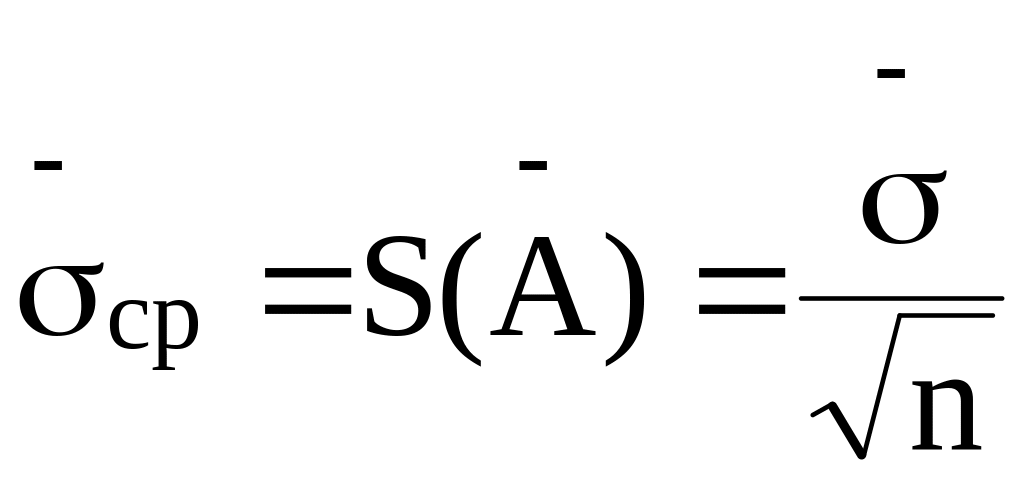(1.13)

следовательно, с увеличением числа измерений n увеличивается точность метода и результата многократных измерений.