Расчетная часть задачи.

Наиболее широко применяемым методом раскрытия статической неопределимости стержневых и рамных систем является метод сил. В этом методе заданная статически неопределимая система освобождается от дополнительных связей и их действие заменяется силами или моментами, величины которых подбираются так, чтобы перемещения соответствовали тем ограничениям, которые накладываются на систему отброшенными связями.

Рис. 34

Система, освобожденная от дополнительных связей, становится статически определимой и называется основной системой. В качестве допол­нительной связи для рассматриваемой рамы будет считать горизонтальную связь на левой опоре (рис. 41). По направлению отброшенной связи прикладываем её реакцию - неизвестное уси­лие X₁ . Каноническое уравнение метода сил показывает, что полное пере­мещение в основной системе, возникающее по направлению неизвестного усилия Σ, под влиянием силы и заданной нагрузки Р, равно нулю:

δ₁₁Х₁+∆_1Р=0

Для определения коэффициентов δ₁₁ и ∆_1Р каноническое основная система (рис. 35) поочередно нагружается единичным горизонтальным усилием = 1 (рис. 36) и заданной нагрузкой Р (рис. 43 ). Для каждого вида нагружения строятся эпюры от единичной нагрузки 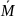,и грузовая М_Р . Путем перемножения эпюры саму на себя и на грузовую эпюру М_Р по правилу Верещагина определяются коэффициенты канонического уравнения.

Рис. 35 Рис. 36

;

.

Подставляя 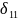и в уравнение σ₁₁Х₁+Σ_1Р=0, получим:

Отсюда

Рис. 37

Входящие сюда величины a, b, l получают непосредствен­ными измерениями на раме, подготовленной для проведения эксперимента. При заданной величине a по формуле определяют горизонталь­ное усилие X₁. Для получения окончательной суммарной эпюры изгибающих моментов ординаты единичной эпюры умножаются на найденное значение X₁ и складываются с соответствующими ординатами грузовой эпюры М_Р моментов (рис. 37). Отсюда видно, что наибольшие изгибающие моменты М_maxвозникают на среднем участке горизонтального стержня рамы и соответствующие нормальные напряжения на Рис. 44 участке рамы,определяемые теоретическим путем, будут

,

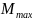- изгибающий момент в середине полета рамы, - осевой момент

сопротивления.

Для прямоугольного сечения высотой h и шириной b₁ (рис. 37) .

Входящие сюда величины получают непосредственными замерами высоты и ширины горизонтального пролета рамы.

(рис.38)

Содержание

ЛАБОРАТОРАНАЯ РАБОТА №1. «Определение механических характеристик стали при растяжении»……………………………………….....2

ЛАБОРАТОРАНАЯ РАБОТА №2. «Определение механических характеристик пластичных и хрупких материалов при сжатии» ………........12

ЛАБОРАТОРАНАЯ РАБОТА №3. «Экспериментальное определение деформаций и напряжений»……………………………………………….....…15

ЛАБОРАТОРАНАЯ РАБОТА №4. «Определение модуля продольной упругости и коэффициента Пуассона»…………………………………….......22

ЛАБОРАТОРАНАЯ РАБОТА №5. «Определение предела прочности материала при срезе»………………………………………………………........24

ЛАБОРАТОРАНАЯ РАБОТА №6. «Определение главных напряжений при кручении тонкостенной трубы»………………………………………..............27

ЛАБОРАТОРАНАЯ РАБОТА №7. «Определение напряжения в балке при изгибе»……………………………………………………………………….......30

ЛАБОРАТОРАНАЯ РАБОТА №8. «Определение деформаций балки при изгибе»……………………………………………………………………….......35

ЛАБОРАТОРАНАЯ РАБОТА №9. «Определение деформаций консольной балки при изгибе»…………………………………………………………....….38

ЛАБОРАТОРАНАЯ РАБОТА №10. «Определение перемещений балки при косом изгибе»…………………………………………………………............…41

ЛАБОРАТОРАНАЯ РАБОТА 11. «Определение напряжений в брусе при внецентренном растяжении»……………………………………………....…...43

ЛАБОРАТОРАНАЯ РАБОТА 12. «Демонстрация теоремы о взаимности перемещений»……………………………………………………………....…...46

ЛАБОРАТОРАНАЯ РАБОТА 13. «Определение момента в защемлении статически неопределимой балки»………………………………………....….50

ЛАБОРАТОРАНАЯ РАБОТА 14. «Определение горизонтальной реакции опоры и напряжений в статически неопределимой раме»……………….......55