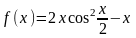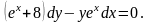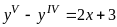- •Учебные материалы для студентов заочной формы обучения
- •2 Семестр
- •3 Семестр
- •Форма промежуточного контроля – зачет Вопросы для подготовки к зачету
- •2 Семестр изучения дисциплины Форма текущего контроля – контрольная работа № 2
- •Форма промежуточного контроля – экзамен
- •Вопросы для подготовки к экзамену
- •Критерии формирования оценок экзамена
- •3 Семестр изучения дисциплины Форма текущего контроля – контрольная работа № 3
- •Форма промежуточного контроля – экзамен
- •Вопросы для подготовки к экзамену
- •Критерии формирования оценок экзамена
- •Учебно-методическое и информационное обеспечение дисциплины
- •Базы данных, информационно-справочные и поисковые системы
Форма промежуточного контроля – экзамен
Экзаменационный билет включает в себя пять заданий:
два теоретических вопроса;
три практических задания.
Вопросы для подготовки к экзамену
Понятие функции нескольких переменных. Предел и непрерывность функции нескольких переменных. Частные производные. Производная по направлению. Градиент.
Дифференцируемость. Производные сложной функции. Касательная плоскость и нормаль к поверхности. Производные и дифференциалы высших порядков.
Экстремумы функции нескольких переменных. Условные экстремумы.
Понятие двойного интеграла. Его свойства. Вычисление.
Тройной интеграл. Его свойства. Вычисление.
Замена переменных в кратных интегралах.
Криволинейный и поверхностный интегралы первого рода.
Криволинейный интеграл второго рода.
Поверхностный интеграл второго рода.
Скалярные и векторные поля. Поверхности уровня. Задача о работе силового поля.
Формула Грина. Циркуляция векторного поля.
Поток векторного поля через поверхность.
Формула Остроградского-Гаусса.
Дивергенция. Ротор векторного поля.
Формула Стокса.
Специальные виды векторных полей.
Ротор, дивергенция, оператор Лапласа в цилиндрических и сферических координатах.
Критерии формирования оценок экзамена
Экзамен проводится в устной форме: обсуждается теоретический материал и приводится решение практических заданий с объяснением.
При выставлении оценки учитывается активность студента во время аудиторных занятий, и результаты собеседований по лекционному материалу и материалу практических занятий.
Оценка «отлично» – полный, развернутый ответ на все вопросы билета.
Оценка «хорошо» – полный ответ на любые четыре вопроса билета.
Оценка «удовлетворительно» – дан ответ на любые три вопроса.
Оценка «неудовлетворительно» – ставится в случае, если студент не выполнил ни одного практического задания или ответил только на один теоретический и один практический вопрос из пяти предложенных.
3 Семестр изучения дисциплины Форма текущего контроля – контрольная работа № 3
Номер варианта контрольной работы определяется по номеру фамилии студента в списке зачисления по данному направлению.
Контрольная работа выполняется в рукописном виде в тетради. Оформление письменной работы согласно МИ 4.2-5/47-01-2013 Общие требования к построению и оформлению учебной текстовой документации.
Задание 1. Исследовать на сходимость ряд.
1 |
4)
|
2 |
5)
|
3 |
4)
|
4 |
5)
|
5 |
4)
|
6 |
4)
|
7 |
5) ; 6) |
8 |
5) ; 6) |
9 |
5) ; 6) |
10 |
5)
|
11 |
5)
|
12 |
5)
|
13 |
5)
|
14 |
4)
|
15 |
4)
|
16 |
5)
|
17 |
5)
|
18 |
5)
|
19 |
5)
|
20 |
4)
|
Задание 2. Найти область сходимости функционального ряда
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
Задание 3. Найти область сходимости степенного ряда. Исследовать поведение ряда в граничных точках области сходимости.
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
Задание
4. Разложить
функцию в ряд Тейлора по степеням
 .
.
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
Задание 5. Найти общий интеграл дифференциального уравнения.
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
Задание 6. Найти общий интеграл дифференциального уравнения.
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
Задание 7. Найти частное решение дифференциального уравнения.
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
Задание 8. Найти общее решение дифференциального уравнения.
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
Задание 9. Найти общее решение дифференциального уравнения.
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|

 ;
2)
;
2)
 ;
3)
;
3)
 ;
; ;
5)
;
5)
 ;
6)
;
6)

 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
; ;
6)
;
6)

 ;
2)
;
2)
 ;
3)
;
3)
 ;
; ;
5)
;
5)
 ;
6)
;
6)

 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
; ;
6)
;
6)

 ;
2)
;
2)
 ;
3)
;
3)
 ;
;
 ;
5)
;
5)
 ;
6)
;
6)

 ;
2)
;
2)
 ;
3)
;
3)
 ;
;
 ;
5)
;
5)
 ;
6)
;
6)
 ;
2)
;
3)
;
4)
;
;
2)
;
3)
;
4)
; ;
4)
;
4)
 ;
; ;
6)
;
6)

 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
; ;
6)
;
6)

 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
; ;
6)
;
6)

 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
; ;
6)
;
6)
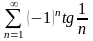
 ;
2)
;
2)
 ;
3)
;
3)
 ;
;
 ;
5)
;
5)
 ;
6)
;
6)

 ;
2)
;
2)
 ;
3)
;
3)
 ;
; ;
5)
;
5)
 ;
6)
;
6)

 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
; ;
6)
;
6)

 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
; ;
6)
;
6)

 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
; ;
6)
;
6)

 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
; ;
6)
;
6)

 ;
2)
;
2)
 ;
3)
;
3)
 ;
; ;
5)
;
5)
 ;
6)
;
6)

 ;
;


 ;
;

 ;
;

 ;
;

 ;
;

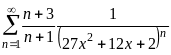 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;

 ;
;