
- •Учебные материалы для студентов заочной формы обучения
- •2 Семестр
- •3 Семестр
- •Форма промежуточного контроля – зачет Вопросы для подготовки к зачету
- •2 Семестр изучения дисциплины Форма текущего контроля – контрольная работа № 2
- •Форма промежуточного контроля – экзамен
- •Вопросы для подготовки к экзамену
- •Критерии формирования оценок экзамена
- •3 Семестр изучения дисциплины Форма текущего контроля – контрольная работа № 3
- •Форма промежуточного контроля – экзамен
- •Вопросы для подготовки к экзамену
- •Критерии формирования оценок экзамена
- •Учебно-методическое и информационное обеспечение дисциплины
- •Базы данных, информационно-справочные и поисковые системы
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Забайкальский государственный университет»
(ФГБОУ ВО «ЗабГУ»)
Факультет энергетический
Кафедра информатики, вычислительной техники и прикладной математики
Учебные материалы для студентов заочной формы обучения
(с полным сроком обучения)
по дисциплине «Математический анализ»
для направления подготовки 09.03.01 Информатика и вычислительная техника
Общая трудоемкость дисциплины – 14 зачетных единиц.
Форма текущего контроля в семестре – контрольная работа.
Курсовая работа (курсовой проект) (КР, КП) – нет.
Форма промежуточного контроля в семестре – зачет/экзамен/экзамен.
Чита 2016 г.
Краткое содержание курса
1 семестр
Раздел 1. Введение в анализ.
Раздел 2. Дифференциальное исчисление функций одной переменной.
Раздел 3. Интегральное исчисление функции одной переменной.
2 Семестр
Раздел 4. Функции нескольких переменных.
Раздел 5. Кратные интегралы.
Раздел 6. Теория поля.
3 Семестр
Раздел 7. Ряды.
Раздел 8. Обыкновенные дифференциальные уравнения.
1 семестр изучения дисциплины
Форма текущего контроля – контрольная работа № 1
Номер варианта контрольной работы определяется по номеру фамилии студента в списке зачисления по данному направлению.
Контрольная работа выполняется в рукописном виде в тетради. Оформление письменной работы согласно МИ 4.2-5/47-01-2013 Общие требования к построению и оформлению учебной текстовой документации.
Задание
№1. Для числа

 найти
найти
 ,
,
 ,
,
 ,
,
 ,
,
 .
Изобразить число
.
Изобразить число
 на комплексной плоскости. Представить
число
в тригонометрической форме.
на комплексной плоскости. Представить
число
в тригонометрической форме.
Вариант |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
Задание 2. Найти области определения указанных функций. Записать используя обозначения, принятые в теории множеств.
Вариант |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
Задание
3. Найти
 для указанных последовательностей
для указанных последовательностей
 .
.
1 |
1)
|
2 |
1)
|
3 |
1)
|
4 |
1)
|
5 |
1)
|
6 |
1)
|
7 |
1)
|
8 |
1)
|
9 |
1)
|
10 |
1)
|
11 |
1)
|
12 |
1)
|
13 |
1)
|
14 |
1)
|
15 |
1)
|
16 |
1)
|
17 |
1)
|
18 |
1)
|
19 |
|
20 |
1) 2)
|
Задание 4. Найти указанные пределы.
1 |
1) 3)
|
2 |
3)
|
3 |
3)
|
4 |
3)
|
5 |
3) 4)
|
6 |
3) 4)
|
7 |
3)
|
8 |
3) |
9 |
3)
|
10 |
3) |
11 |
3)
|
12 |
3)
|
13 |
3)
|
14 |
3)
|
15 |
3) |
16 |
3)
|
17 |
3)
|
18 |
3) 4)
|
19 |
3)
|
20 |
3)
|
Задание 5. Найти точки разрыва функции и указать их тип. Схематично изобразить график в окрестности каждой точки разрыва.
Вариант |
|
1 |
|
2 |
1)
2)
|
3 |
|
4 |
1)
2)
|
5 |
|
6 |
1) 2)
|
7 |
|
8 |
1)
2)
|
9 |
|
10 |
1)
|
11 |
|
12 |
1)
|
13 |
|
14 |
1)
|
15 |
|
16 |
1)
|
17 |
|
18 |
1)
|
19 |
|
20 |
1)
|
Задание
6.
Найти производную
 .
.
1 |
|
2 |
1)
|
3 |
1)
|
4 |
1)
9) |
5 |
1)
|
6 |
1)
|
7 |
1)
|
8 |
1)
|
9 |
8)
9)
10)
|
10 |
1)
|
11 |
1)
|
12 |
|
13 |
1)
|
14 |
|
15 |
|
16 |
1)
|
17 |
|
18 |
|
19 |
1)
|
20 |
|
Задание 7. Найти производную указанного порядка
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
Задание 8. Провести полное исследование функции и построить график (выбрать два за четырех).
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
Задание 9. Найти неопределенные интегралы.
1 |
3)
|
2 |
1) 3)
|
3 |
1)
|
4 |
1)
|
5 |
1) , 2) ,
|
6 |
1) , 2) ,
|
7 |
1) , 2) ,
|
8 |
1) , 2) ,
|
9 |
1) , 2) ,
|
10 |
1) , 2) ,
|
11 |
1) , 2) ,
|
12 |
1) , 2) ,
|
13 |
1) , 2) ,
|
14 |
1) , 2) ,
|
15 |
1)
, 2)
|
16 |
1) , 2) ,
|
17 |
1) , 2) ,
|
18 |
1) , 2) ,
|
19 |
1) , 2) ,
|
20 |
1) , 2) ,
|
Задание 10. Вычислить определенные интегралы.
1 |
4) 6)
|
2 |
3)
5)
6)
|
3 |
3) 5) 7)
|
4 |
3)
7)
|
5 |
4)
7)
|
6 |
4)
6)
|
7 |
4) 6)
|
8 |
1)
4) 6)
|
9 |
3)
|
10 |
4)
6)
|
11 |
3)
5)
7)
|
12 |
3)
5)
|
13 |
1)
4) 6)
|
14 |
3)
5)
|
15 |
3)
|
16 |
3)
6)
|
17 |
3) , 4) ,
7) |
18 |
3) , 4) , 5) , 6) , 7) |
19 |
3) , 4) ,
7)
|
20 |
1)
5)
7)
|














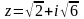


























 ,
2)
,
2)

 2)
2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 ,
2)
,
2)

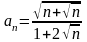 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)
 , 2)
, 2)
 , 2)
, 2)
 ,
,

 ,
,

 , 2)
, 2)
 ,
,
 ,
4)
,
4)

 , 2)
, 2)
 ,
, ,
4)
,
4)

 , 2)
, 2)
 ,
,
 ,
4)
,
4)

 , 2)
, 2)
 ,
,
 , 4)
, 4)

 , 2)
, 2)
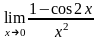 ,
,
 ,
,
 , 2)
, 2)
 ,
,
 ,
,

 , 2)
, 2)
 ,
,
 , 4)
, 4)

 ,2)
,2)
 , 4)
, 4)

 , 2)
, 2)
 ,
, , 4)
, 4)

 , 2)
, 2)
 ,
, , 4)
, 4)

 , 2)
, 2)
 ,
, , 4)
, 4)

 , 2)
, 2)
 ,
, , 4)
, 4)

 , 2)
, 2)
 ,
, , 4)
, 4)

 , 2)
, 2)
 ,
, , 4)
, 4)

 , 2)
, 2)
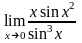 ,
, , 4)
, 4)

 , 2)
, 2)
 ,
, , 4)
, 4)

 , 2)
, 2)
 ,
, , 4)
, 4)

 , 2)
, 2)
 ,
, ,
,
 , 2)
,
, 2)
, , 4)
, 4)

 , 2)
, 2)
 ,
, , 4)
, 4)

 ,
,
 ,
,
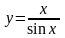 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 , 2)
, 2)

 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 ,
, , 10)
, 10)

 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 ,
, ,
,
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, ,
, ,
, ,
, ,
,
 ,
, ,
,
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
;
 ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
;
 ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
;

 ;
; ;
; ;
; ;
;
 ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;
 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
;
 ;
;
 ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.







































 ,
2)
,
2)
 ,
, ,
,
 ,
5)
,
5)

 , 2)
, 2)
 ,
, ,
, ,
5)
,
5)
 , 2)
, 2)
 ,
, ,
, ,
5)
,
5)
 , 2)
,
, 2)
, ,
, ,
, ,
5)
,
5)
 ,
, ,
, ,
5)
,
5)
 ,
, ,
3)
,
3)
 ,
, , 5)
, 5)
 ,
, , 7)
, 7)

 ,
2)
,
2)
 ,
, ,
4)
,
4)
 ,
, ,
, , 7)
, 7)

 ,
2)
,
2)
 ,
, , 4)
, 4) ,
, ,
6)
,
6)
 ,
,
 ,
2)
,
2)
 ,
, , 4)
, 4) ,
, ,
6)
,
6)
 ,
,
 ,
, ,
3)
,
3)
 ,
, ,
, ,
6)
,
6)
 ,
,
 ,
, ,
3)
,
3)
 ,
, , 5)
, 5)
 ,
,
 , 7)
, 7)

 ,
, ,
3)
,
3)
 ,
, , 5)
, 5) ,
, ,
7)
,
7)

 ,
, ,
3)
,
3) ,
, ,
5)
,
5)
 ,
, , 7)
, 7)

 ,
2)
,
2)
 ,
, ,
4)
,
4) ,
, ,
6)
,
6)
 , 7)
, 7)

 ,
, ,
3)
,
3)
 ,
, , 5)
, 5)
 ,
, ,
7)
,
7)

 ,
2)
,
2)
 ,
, , 4)
, 4)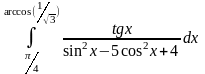 ,
, ,
6)
,
6)
 ,
,
 ,
2)
,
2)
 ,
, ,
4)
,
4)
 ,
, ,
,
 ,
7)
,
7)

 ,
, ,
3)
,
3)
 ,
, , 5)
, 5) ,
,
 , 7)
, 7)

 ,
2)
,
2)
 ,
, , 4)
, 4)
 ,
, ,
6)
,
6)
 , 7)
, 7)

 ,
2)
,
2) ,
, ,
4)
,
4) ,
, ,
6)
,
6)
 , 7)
, 7)

 ,
2)
,
2)
 ,
, ,
, ,
5)
,
5)
 ,
,
 ,
7)
,
7)

 ,
2)
,
,
2)
, ,
2)
,
,
2)
,
 , 2)
, 2)
 ,
, ,
4)
,
4) ,
, , 6)
, 6)
 ,
,