10 Клас

10.1 Відповідь.28.

10.2. Відповідь. .

Оскільки – корінь рівняння , то , тобто Тому . Таким чином,

.

10.3. Відповідь. і . .

Якщо десятковий запис числа містить не більше трьох цифр, то сума цих цифр не перевищує . Отже, . Тому, – чотирицифрове число, перша цифра якого дорівнює або . Якщо перша цифра числа дорівнює , то і . Нехай , де – цифра, тоді . Звідки . Нехай , тоді . Якщо перша цифра числа дорівнює , то перевіривши числа від до , знаходимо ще одне значення .

10.4. Відповідь. .

Н ехай , тоді як кути при основі рівнобедреного трикутника. за умовою задачі; як вписані кути, що спираються на одне і ту саму дугу. Крім того, помічаємо, що . Тоді трикутники і рівні за двома сторонами і кутом між ними. Отже, .

10.5. Скористаємося методом математичної індукції.

1) При одержуємо правильну нерівність: .

2) Припустимо, що доводжувана нерівність правильна для , тобто . Доведемо, використовуючи припущення, що доводжувана нерівність буде правильною і при . Дійсно,

,

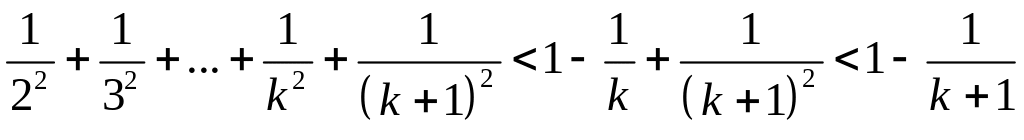бо .

Отже, задана нерівність виконується при всіх натуральних .

11 Клас

11.1. Відповідь.21.

11.2. Відповідь. .

Нехай і - вершини трикутника. Оскільки , то і . За теоремою Піфагора маємо .

11.3. Відповідь. , де .

Нехай , а , де і – цілі числа. Використовуючи формулу для тангенса подвійного аргументу, одержимо: . Звідки випливає, що . Якщо , то число взаємно просте з числами і . Тому, для того щоб число було цілим, потрібно щоб число було цілим. Звідки випливає, що або . Отже, , але тоді і . Розв’язавши рівняння , знаходимо, що , де .

11.4. Оскільки – центр вписаного кола трикутника , то прямі і – бісектриси кутів і . Тому,

.

О тже, як зовнішній кут трикутника . Оскільки точки , , , лежать одному колі, то (як вписані кути, що спираються на одну й ту саму дугу). Звідки (як суміжний кут до кута ). Таким чином, , тобто чотирикутник – вписаний, що і треба було довести.

11.5. Розглянемо різницю між лівою і правою частинами даної нерівності і доведемо, що вона невід’ємна. Дійсно,

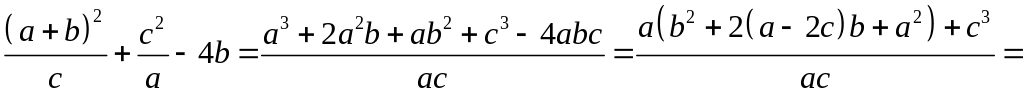
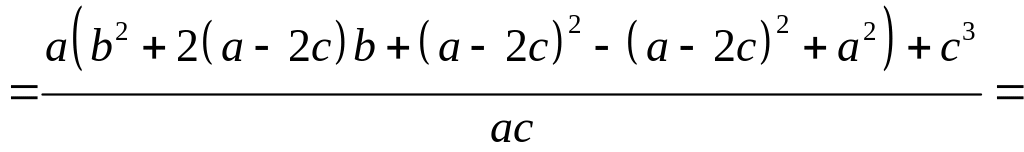
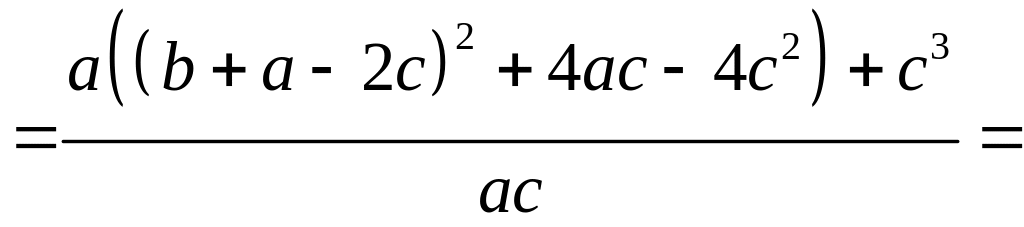
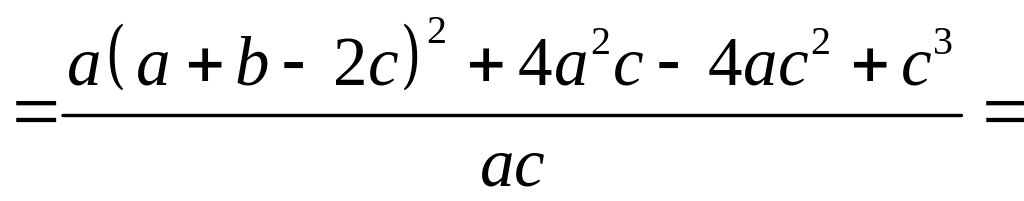
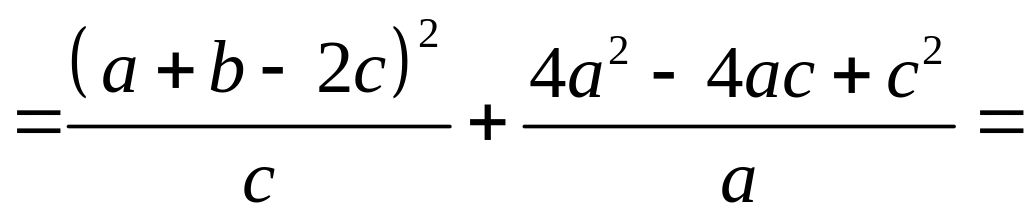
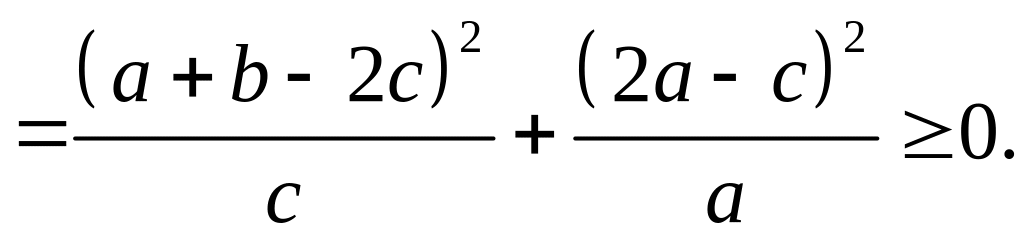
6 клас

1. Четверо білочок з’їли 2005 горішків, причому кожна з’їла не менше 100. Перша білочка з’їла більше, ніж інші. Друга й третя з’їли разом 1269 горішків. Скільки горішків з’їла перша білочка?

2. Зафарбуйте декілька клітинок у квадраті 10 10 так, щоб у кожної клітинки було рівно дві сусідні за стороною зафарбовані клітинки.

3. Тетянка сказала: «У Андрійка більше ста книг». Данилко заперечив: «Ні, менше». Марійка сказала: «Ну, хоча б одна книга у нього напевне є». Скільки книг може бути у Андрійка, якщо з цих трьох тверджень рівно одне істинне?

4. Маємо 2004 сірники. За один хід можна взяти будь-яку кількість від 1 до 5 сірників. Грають двоє. Програє той, хто не може зробити хід. Хто з двох гравців – перший чи другий, може забезпечити собі виграш?

5. Доведіть, що серед довільних 2005 натуральних чисел знайдуться два такі, що їх різниця ділиться на 2004.