Методические указания по выполнению контрольных работ

Задача №1.

Даны матрицы

1. Вычислить матрицу 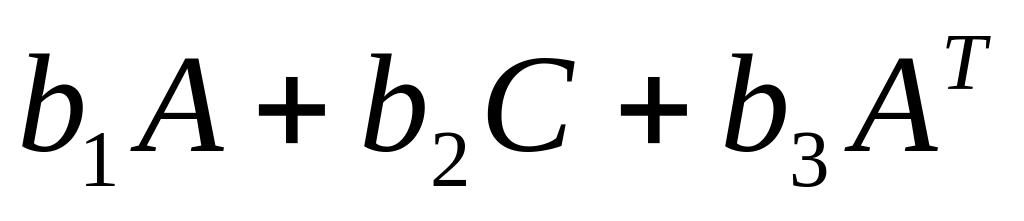( - транспонированная матрица)

2. Вычислить определители

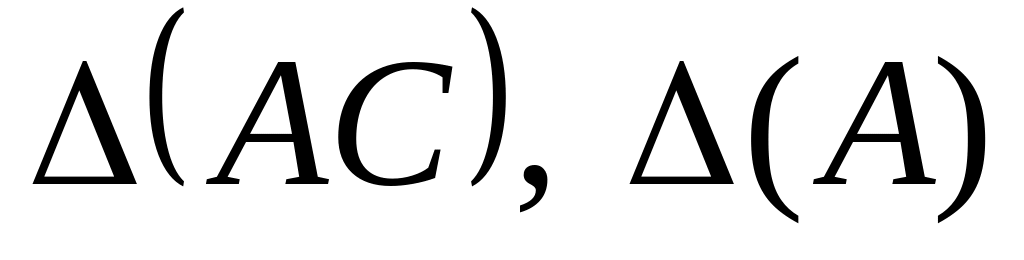
3. Для матрицы А найти обратную , используя алгебраические дополнения, и проверить, что

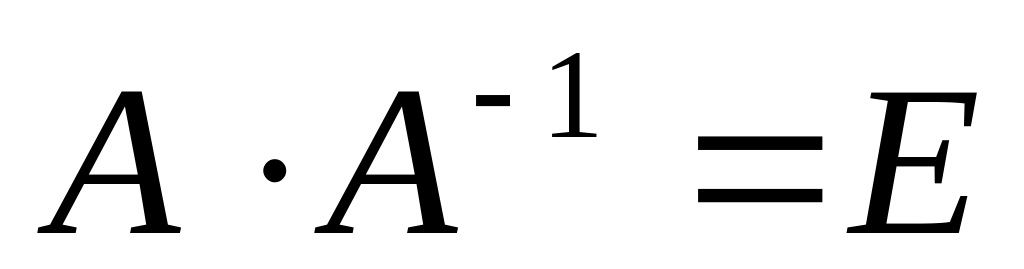
4. Записать систему уравнений 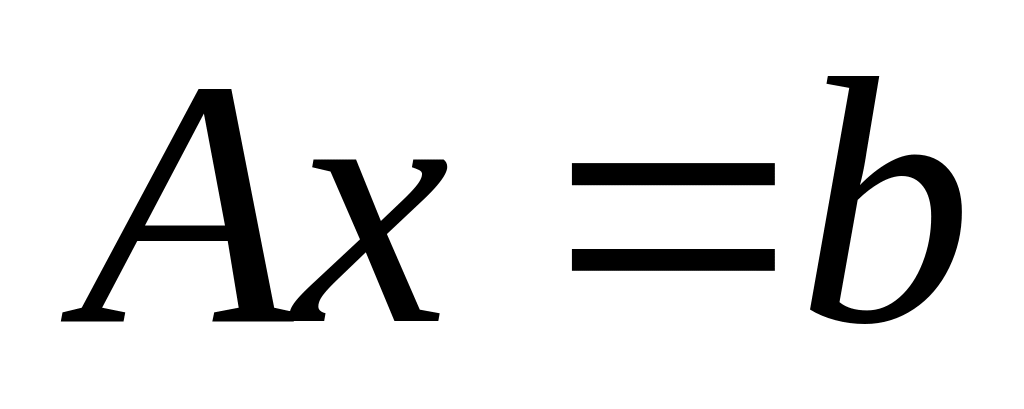и решить её матричным методом (используя найденную матрицу ) и методом Крамера.

Решение:

1. 

1. 

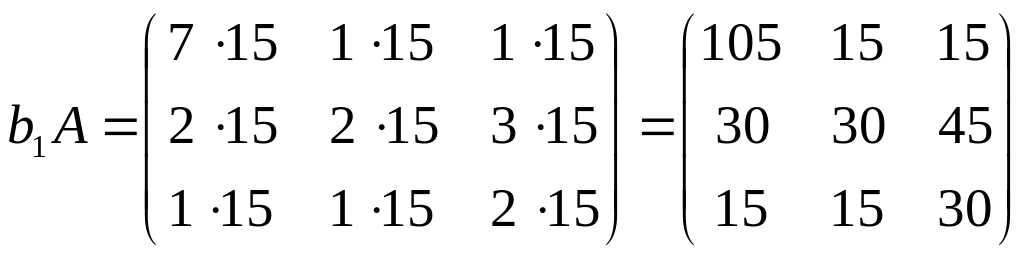
Вычислить определители

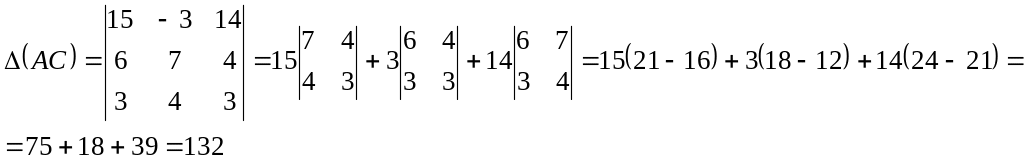
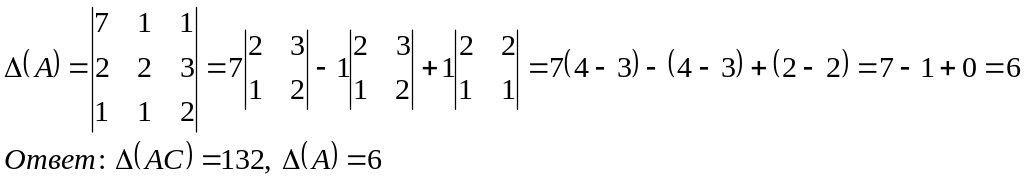
2. Для матрицы А найти обратную используя алгебраические дополнения, и проверить, что

Так как , значит матрица существует.

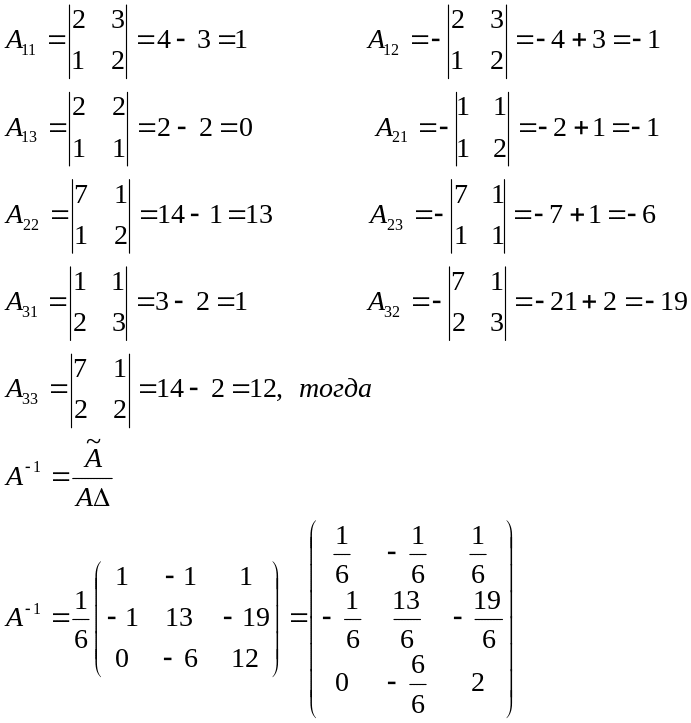
Проверим условие

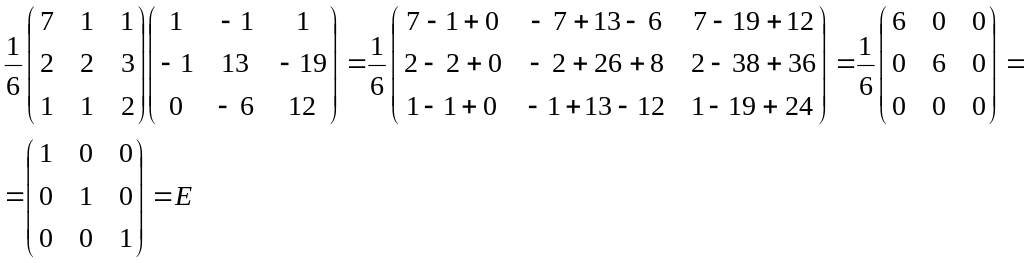
3. Записать систему уравнений 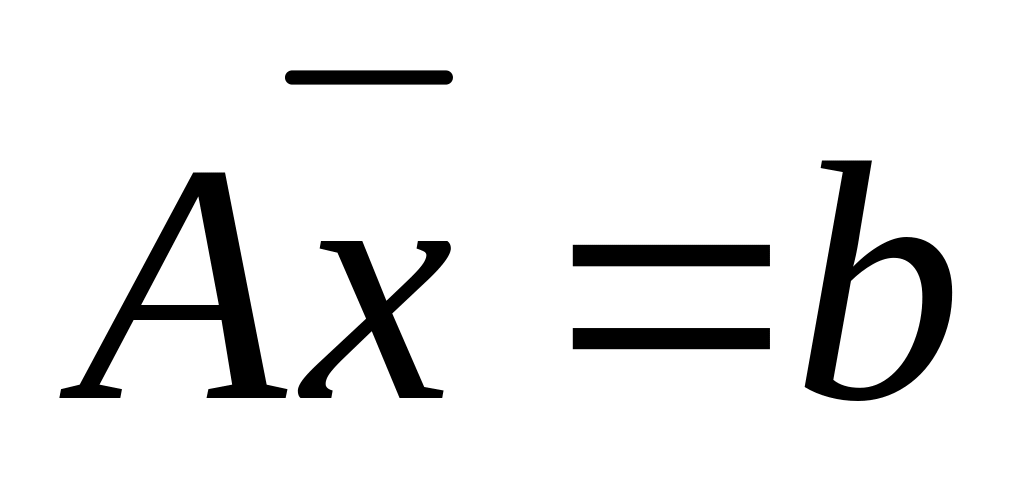и решить её, матричным методом используя 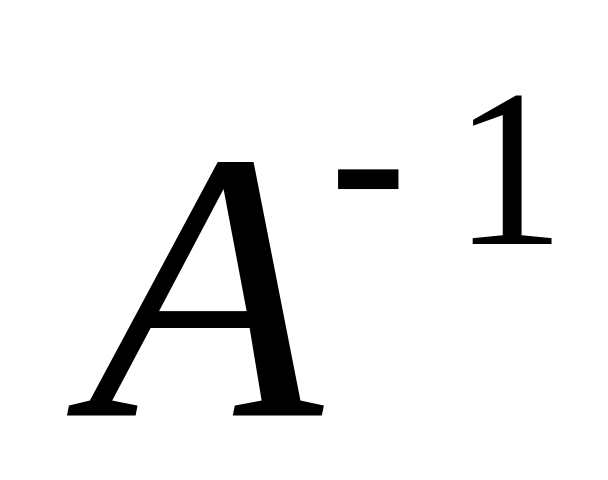и методом Крамера

а. матричным методом

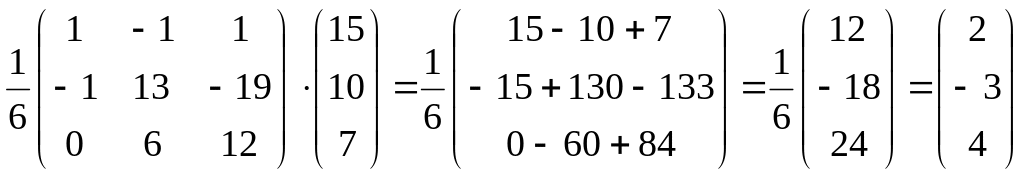
Проверка

б. Метод Крамера

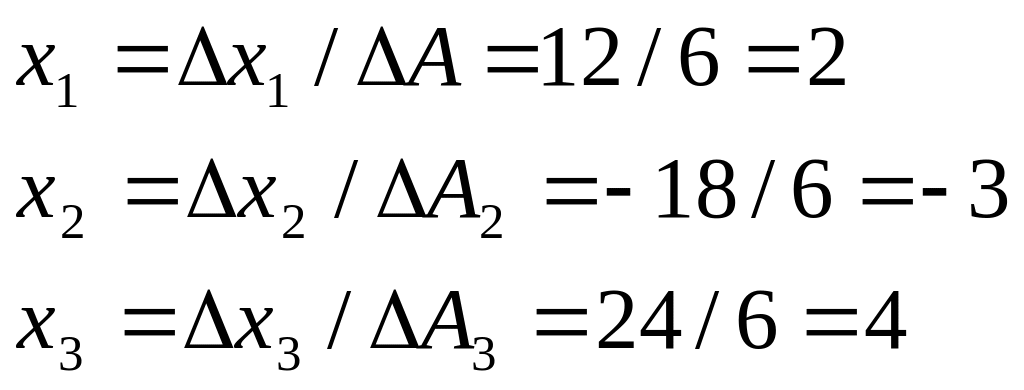
Ответ:

Задача №2. Найти пределы: a) ; б) в)

г) д) е) ж)

Решение:

a)

б)

в)

г)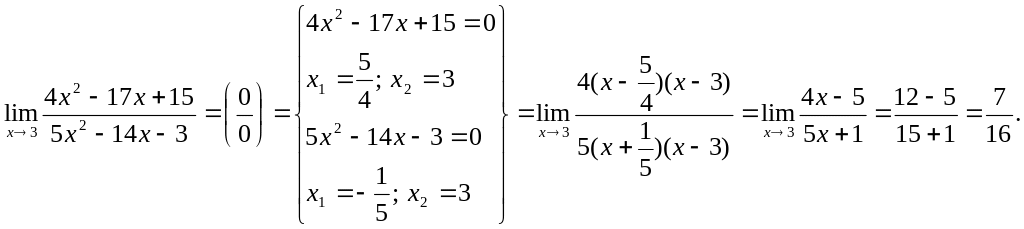

д)

е)

ж)

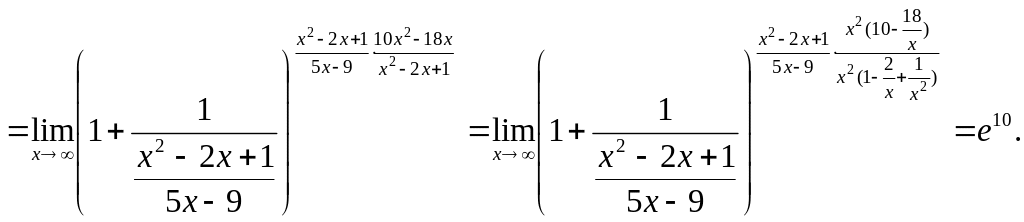
Задача №3. Найти производную функции:

1. а)

Используем правила и , а также формулы таблицы дифференцирования.

б)

Используем правила , а также формулы таблицы дифференцирования.

с)

Прологарифмируем обе части данной функции.

Продифференцируем обе части последнего равенства:

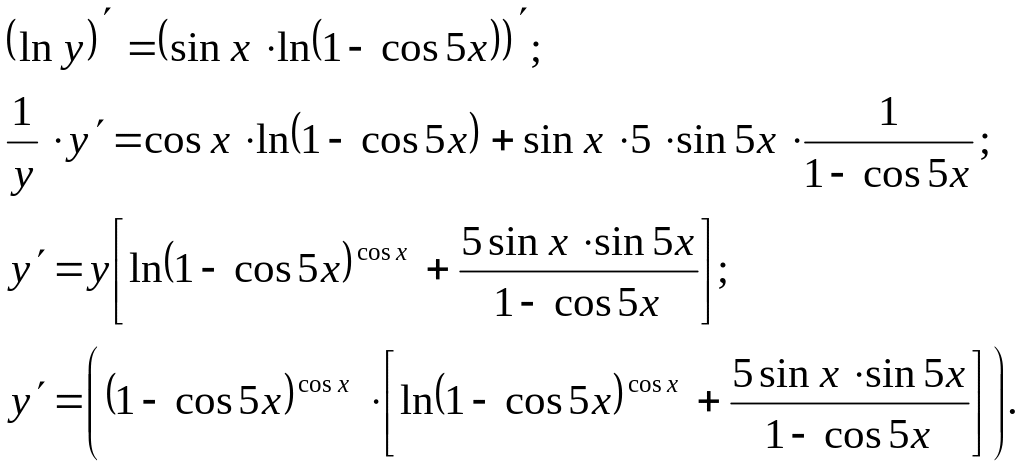
2. Найти и : а) б)

а)

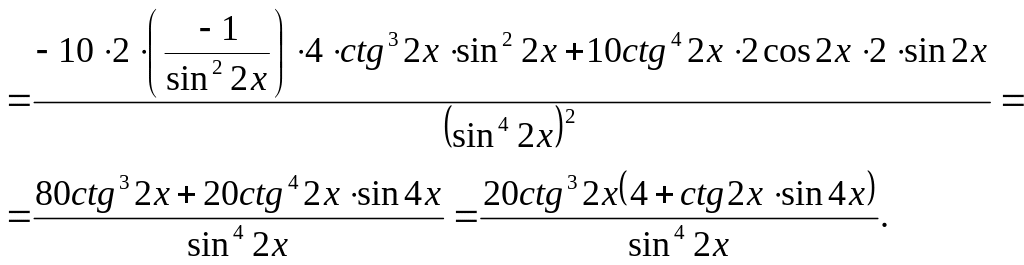
б)

Найдём производные и параметрически заданной функции

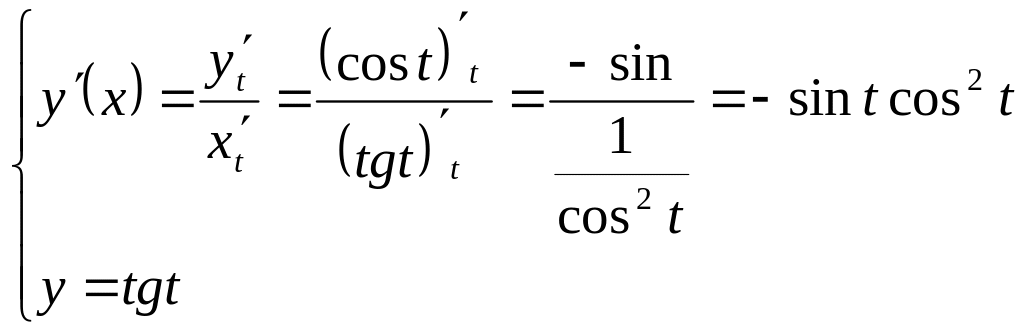
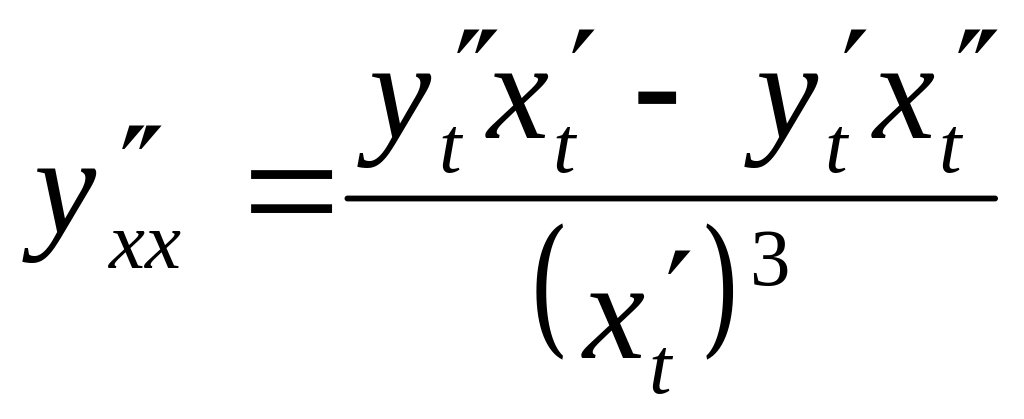
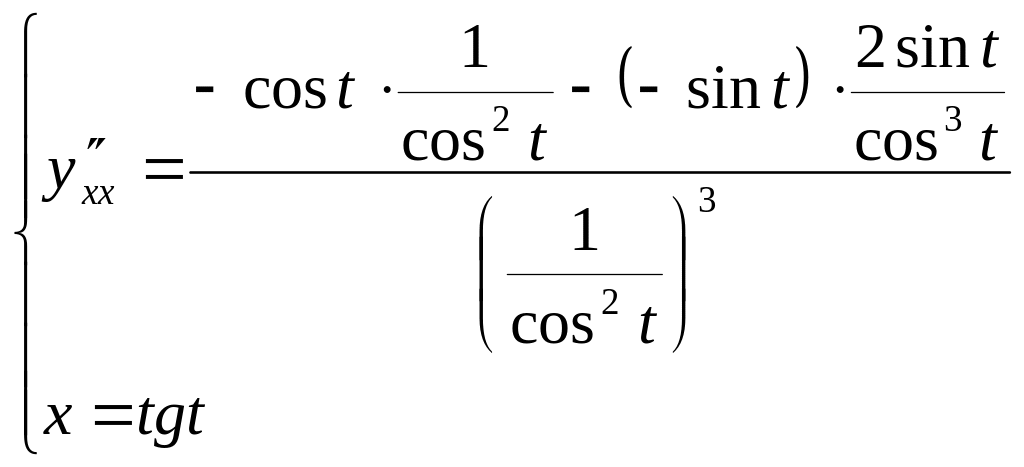
Задача №4. Для функции z = f(x,y) в точке А(x₀,y₀) найти градиент и производную в направлении вектора

A(1;-2);

Решение:

Задание 5. Найти интервалы монотонности и экстремумы функции

Решение:

- стационарные точки

Функция убывает при , возрастает при .

Точка не является точкой экстремума, т.к. производная не меняет знак при переходе через эту точку.

Точка - точка минимума.

- минимум функции.

Задание 6. Задана функция спроса . Найти эластичность при заданных значениях цены или количества товара. ,

Решение:

Если это функция спроса, то эластичность вычисляется по формуле

Из уравнения функции спроса найдем значение при :

;

;

.

Тогда .

Литература:

1. Кремер Н.Ш. Высшая математика для экономического бакалавриата: учебник и практикум. М.: Юрайт, 2013.

2. Пискунов Н.С., Дифференциальное и интегральное исчисления. т.1. М: Наука, 2004

3. Пискунов Н.С., Дифференциальное и интегральное исчисления. т.2. М: Наука, 2004

4. Барвин И.И., Математический анализ. Учебник для вузов, М. Высшая школа, 2006

5. Данко П.Е., Высшая математика в упражнениях и задачах, Оникс, 2006

6. Б.В. Соболь, Н.Т. Мишняков, В.М. Поркешеян, Практикум по высшей математике. Феникс, 2006

7. Общий курс высшей математики для экономистов. Под ред. Ермакова В.М. М.: Инфра-М, 2010

8. Сборник задач по высшей математике для экономистов. Под ред. Ермакова В.М. М.: Инфра-М, 2009

9. Бугров Я.С. и др. Высшая математика в 3 т. Т.1. Элементы линейной алгебры и аналитической геометрии. Феникс, 1997

10. Бугров Я.С. и др. Высшая математика в 3 т. Т.2. Дифференциальное и интегральное исчисление. Феникс, 1997

11. Шипачев В.С. Высшая математика. М: Юрайт, 2013

12. Шипачев В.С. Задачник по высшей математике. М: Высш.шк., 2003

13. Чумак И.В. Дифференциальные уравнения. Ростов-на-Дону, ИЦ ДГТУ, 2007