Определение случайного процесса.

Пусть задано множество Ω — множество элементарных исходов и некоторое множество T, являющееся подмножеством множества вещественных чисел, то есть T ⊂ R. Будем называть случайной функцией вещественную числовую функцию двух аргументов ω ∈ Ω и t ∈ T. Обозначим случайную функцию ξ(w, t). Если аргумент t принимает смысл времени t ≥ 0, то случайную функцию будем называть случайным процессом.

Классификация случайных процессов

Случайная величина ξ имеет дискретный тип распределения, а значит все сечения случайного процесса в этом примере являются дискретными случайными величинами. В этом случаи процесс называют дискретным. Если сечения имеют непрерывный тип распределения, то случайный процесс называют непрерывным. Кроме того, в примере 7.1.1 время является непрерывной переменной. В этом случае говорят, что рассматривается случайный процесс с непрерывным временем. Если переменная t принимает отдельные дискретные значения, то случайный процесс является процессом с дискретным временем .

Если множество состояний не может быть пронумеровано, то имеем случайный процесс с непрерывными состояниями или просто  непрерывный случайный процесс, для которого характерен плавный переход из состояния в состояние и который задаётся в виде непрерывной функции времени: E(t) (рис.5.1,б). Например, процесс изменения температуры некоторого объекта может рассматриваться как случайный процесс с непрерывными состояниями.

Если промежуток времени между переходами из состояния в состояние является случайным и переход возможен в любой заранее не известный момент времени t, то процесс называется случайным процессом с непрерывным временем.

Процессы с дискретным временем называются стохастическими последовательностями или случайными цепями.

Случайные процессы с дискретными состояниями могут изображаться в виде графа переходов (состояний), в котором вершины соответствуют состояниям, а ориентированные дуги – переходам из одного состояния в другое.

Граф переходов называется размеченным, если на дугах графа указаны условия перехода в виде вероятностей переходов (для процессов с дискретным временем) или интенсивностей переходов (для процессов с непрерывным временем).

Состояния Ei могут быть:

q    невозвратными, если процесс после какого-то числа переходов непременно покидает их;

q    поглощающими, если случайный процесс, достигнув этих состояний прекращается.

Случайный процесс называется транзитивным, если из любого состояния можно перейти за то или иное число шагов в любое другое состояние и вернуться в исходно

ля случайных процессов с непрерывным временем время между переходами из одного состояния в другое случайно. Это означает, что вероятность перехода из одного состояния в другое не может быть задана, поскольку вероятность такого перехода точно в произвольный момент времени t равна нулю. Для описания переходов между состояниями случайного процесса с непрерывным временем вместо вероятностей переходов вводится параметр, называемый интенсивностью перехода.

Интенсивность перехода gij из состояния Ei в состояние Ej определяется как предел отношения вероятности перехода Pij () системы за промежуток времени  из Ei в Ej к длине этого промежутка:

Отсюда следует, что вероятность перехода за бесконечно малый промежуток времени  равна: gij  (iнеравноj) . Вероятность двух и более переходов за время  имеет порядок ()^2 и выше и предполагается бесконечно малой величиной.

Если интенсивности переходов постоянны и не зависят от времени t, то есть от того, в какой момент начинается промежуток , то марковский процесс называется однородным. Если интенсивности gij представляют собой функции времени t, процесс называется неоднородным.

 СЛУЧАЙНЫЕ ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ

5.3.1. Вероятностные характеристики.

Из определения случайного процесса   с независимыми приращениями, приведенного в п.5.1.5, получаем следующее представление процесса

Дисперсия процесса в момент времени   представляет монотонно возрастающую функцию, так как при независимых приращениях из (5.31) следует

Используя известные свойства характеристической функции суммы независимых случайных величин (см. п. 3.3.6), запишем  -мерную характеристическую функцию процесса с независимыми приращениями

где

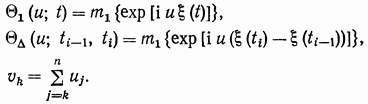
Таким образом, характеристическая функция любого порядка случайного процесса с независимыми приращениями определяется его одномерной и двумерной характеристическими функциями.

5.3.2. Однородные процессы с независимыми приращениями.

Случайный процесс   с независимыми приращениями называется однородным (иногда — процессом со стационарными независимыми приращениями), если он определен при  , причем   и распределение приращения   совпадает с распределением   для всех  . Однородный процесс с независимыми приращениями непрерывен по вероятности.

Из (5.31), следует, что однородный процесс с независимыми приращениями можно представить конечной суммой одинаково распределенных случайных величин и, следовательно,

5.3.3. Случайные процессы со скачками в фиксированные моменты времени.

Рассмотрим процесс   реализации которого — ступенчатые функции со случайными скачками в фиксированные моменты времени (рис. 5.1). Скачок процесса в один из фиксированных моментов  представляет случайную величину  . Тогда рассматриваемый процесс можно записать в виде суммы

Этот процесс непрерывен по вероятности при всех значениях i за исключением тех фиксированных моментов времени, где появляются случайные скачки. Если скачки g,   представляют совокупностьнезависимых случайных величин, то рассматриваемый процесс является случайным с независимыми приращениями.

5.3.4. Гауссовский процесс с независимыми приращениями.

Если приращения на непересекающихся интервалах времени независимы и распределены по нормальному закону, то процесс с независимыми приращениями принадлежит классу гауссовских случайных процессов.

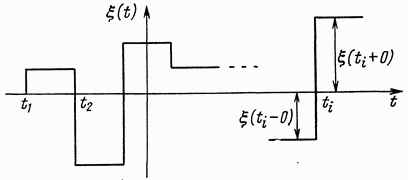
Рис. 5.1. Процесс со случайными скачками в фиксированные моменты времени

Характеристическая функция такого процесса

где

Характеристическая функция приращения этого процесса

где

Так как ад   то из (5.39), (5.40) следует общая формула (5.33).

5.3.5. Винеровский случайный процесс.

Частным случаем гауссовского случайного процесса с независимыми приращениями являетсявинеровский процесс, для которого

Одномерная и двумерная характеристические функции винеровского процесса

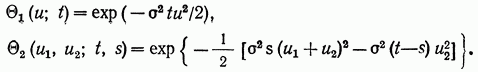
Из (5.43) находим корреляционную функцию винеровского процесса

Винеровский процесс с параметром   называют стандартным.

Реализации винеровского процесса непрерывны, но недифференцируемы в любой момент времени с вероятностью единица (см., например, [15]). Винеровский процесс часто называют процессомброуновского движения, так как он служит математической моделью хаотического перемещения частиц под ударами молекул жидкости.