20. Друга теорема двоїстості.

Двоиста зад – зад ЛО, при чём между решением прямой или двоистой существ связи на основании котор можно делать предположение про опт решение и с-му огран второй. Соотвеств связи устан-ся через теорему двоистости.1.Если в оптимальной точке одной из двойственных задач какое-либо ограничение выполняется как строгое неравенство, то соответствующие переменные двойств. задачи в оптимальной точке равны нулю: а) ∑aijxij<bi→yi*=0; б) ∑aijxij<cj→xj*=0.Экон. смысл: ограничения исходной задачи, имеющие в оптимальной точке вид строгого неравенства, означает, что объем используемого ресурса меньше его запасов, т.е. ресурс является недефицитным и его ценность равна нулю. 2.Если некоторые переменная в оптимальном решении одной из задач строго положительна, то соответственные ей ограничения двойственной задачи в оптимальной точке выполняется как строгое равенство: а) xj*>0→∑aijyi*=Ci;

б) yi*>0→∑aijxi=Bi. Экон. смысл: а) производство j-вида продукции выгодно следовательно сумма оценок затрат и ресурсов равна стоимости реализации; б) ценность Yi-ресурса >0, следовательно данный ресурс является дефицитным и его запасы используются полностью.

Используя теоремы двойственности и зная оптимальное решение одной из двойственных задач можно построить (определить) оптимальное решение двойственной задачи.

21. Транспортна задача. Основні поняття, визначення та математична модель.

Транспортна задача - завдання визначення оптимального плану перевезень однорідного вантажу з n пунктів відправлення в m пунктів споживання. В якості критеріїв оптимальності виступає мінімізація витрат.

Bj (j = 1, м) - Кількість вантажу в пункті відправлення Ai позначається аi (i=1,n)а потреби вантажу в пункті призначення Bj – bj (j=1,m). Тарифи на перевезення задаються матрицею Сij.

Z=C11*X11+C21*X21…+Cn1*Xn+…+C1m*X1m+…+Cnm*Xnm =

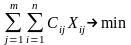
Ограничения будут такими:

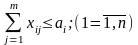
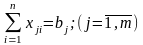
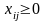
Якщо сумарні запаси рівні сумарним потребам, то завдання називається закритою (збалансованої). Тоді в обмеженнях скрізь буде знак рівності. Закрита задача завжди можна вирішити. Якщо завдання відкрита, то щоб її збалансувати, треба ввести фіктивного споживача (у разі якщо потреби менше) або постачальника. Тарифи на перевезення буду дорівнюють нулю, а потреби (або запаси) будуть рівні відсутньої різниці.

Число змінних в транспортній таблиці = n*m, а число обмежень n+m. Ранг матриці обмежень = (n+m-1) , що відповідає числу лінійно-незалежних рівнянь. Значить опорний план може містити не більше ніж n+m-1 відмінних від нуля невідомих. Якщо їх менше, то план вироджений, а якщо стільки ж, то невироджений.

22. Визначення опорного плану транспортної задачі (метод мінімального елементу, метод північно-західного кута).

Метод Північно-західного кута використовують для знаходження довільного опорного плану транспортної задачі

Схема методу:

1) Вважають верхній лівий елемент матриці Х х 11 = хв (1, b1)

Можливі три випадки:

а) якщо a1 <b1, то х11 = а1 і всю першу рядок починаючи з другого елементу заповнюють нулями.

б) якщо a1> b1, то Х11 = b1, а всі решта елементи першого стовпця заповнюють нулями

в) якщо a1 = b1, то х11 = a 1 = b 1, і всі залишилися елементи перших стовпця і рядка заповнюють нулями

На цьому один крок методу закінчується.

2) Нехай вже пророблено до кроків, кm-й крок полягає в наступному.

Визначають верхній лівий елемент незаповненою частині матриці Х. Нехай це елемент хl, m

Тоді вважають хl,m = min(аkl, bkm), где аkl = al - Σxlj , а bkm = bm – Σxim

Якщо аkl < bkm, то заповнюють нулями l -ю рядок починаючи з (m + 1) -го елемента. В іншому випадку заповнюють нулями решту m-го стовпця.

Метод мінімального елемента дозволяє побудувати початковий опорний план транспортної задачі і є варіантом методу північно-західного кута, враховує специфіку матриці С=(cij)m,n. На відміну від методу північно-західного кута даний метод дозволяє відразу отримати досить економічний план і скорочує загальну кількість ітерацій щодо його оптимізації.

Схема методу: елементи матриці С нумерують починаючи від мінімального в порядку зростання, а потім у цьому ж порядку заповнюють матрицю Х0.

Нехай елементом з мінімальним порядковим номером виявився елемент x0ij

Тоді вважають x 0 ij = min (ai, bj)

Можливі три випадки

а) якщо min (ai, bj) = ai,то решту і-й рядки заповнюють нулями;

б) якщо min (a1, b1) = bj,= виданню, то решту J-го стовпця заповнюють нулями.

в) якщо ai = bj, то решту рядка і стовпця заповнюють нулями.

Далі цей процес повторюють з незаповненою частиною матриці.

Нехай елементом з k -м порядковим номером виявився хklm. Тоді min(akl, bkm), де

а k l = al - Σxglj, g = 1..l-1

bkm = bm - Σxuim, u = 1..k-1

Можливі три випадки:

а) аkl < bkm, тогда хklm = аkl і решту рядка l заповнюють нулями;

б) аkl > bkm, тогда хklm = bkmі залишок стовпця m заповнюють нулями;

в) аk = bkm, тоді решту рядка l і стовпця m заповнюють нулями