Бесконечно малые и бесконечно большие функции и их свойства.

Определение: Функция (x) называется бесконечно малой при xx₀, если

Определение: Функция y=f(x) называется ограниченной, если существует такое число  >0, что при  .

Определение: Функция f(x) называется бесконечно большой при xx₀, если .

1. Сумма двух или конечного числа б/м есть бесконечно малая.

2. Произведение двух или конечного числа б/м есть бесконечно малая.

3. Произведение б/м на ограниченную функцию есть б/м.

Замечание: Частное двух б/м является неопределенностью вида .

4. Сумма конечного числа б/б есть б/б.

5. Произведение конечного числа б/б есть б/б.

6. Произведение б/б на любую не б/м есть б/б.

Замечание: Разность двух б/б является неопределенностью вида (-).

Замечание: Частное двух б/б является неопределенностью вида .

Замечание: Произведение б/б на б/м является неопределенностью вида .

7. Частное от деления б/б на ограниченную функцию есть б/б.

8. Б/м и б/б ‒ взаимообратные функции.

Теорема о представлении функции, имеющей предел:

Для того чтобы число А было пределом функции f(x) при xx₀ , необходимо и достаточно, чтобы в некоторой окрестности точки x₀ f(x) была представима следующим образом: f(x)=A+(x), где (x) – б/м при

Арифметические операции с пределами.

Теорема 1: Пусть , а , тогда

Теорема 2: Пусть , а тогда .

Теорема 3: Пусть , а , тогда , где B0.

Следствие: , где C-const.

Теоремы о предельном переходе в неравенствах.

Теорема 1. Теорема о «двух милиционерах». Пусть заданы 3 функции f(x), (x), g(x) такие, что f(x)(x)g(x). Тогда если и , то

Теорема 2: Пусть функция f(x)0 и существует конечный предел . Тогда A0.

Теорема 3: Если f(x)g(x) и , , то

Первый замечательный предел.

Второй замечательный предел. ;

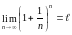Следствия из второго замечательного предела.

1. ; 2. ; ; 3.

Сравнение бесконечно малых.

Рассмотрим отношение двух б/м (x) и (x), т.е. (x) и (x) 0 при xx₀.

Определение: Если , тогда б/м (x) и (x) называются б/м одного порядка малости.

Определение: Если , тогда б/м (x) и (x) называются эквивалентными. Обозначаются: (x)~ (x).

Определение: Если , тогда б/м (x) имеет порядок малости выше, чем б/м (x).

Определение: Если , тогда б/м (x) имеет порядок малости выше, чем б/м (x).

Теорема: Если при xx₀ б/м (x)~ *(x), а б/м (x)~ *(x), то ; .

Тогда при xx₀ и (x) ‒ б/м справедливо:

sin(x)~ (x); e^(x)-1~(x); ln(1+(x))~ (x); a^(x)-1~(x)·lna;

tg(x)~ (x); arcsin(x)~ (x); arctg(x)~ (x); (1+(x))^a-1~a·(x).

Непрерывность функции.

Пусть функция y=f(x) определена в точке x₀ и некоторой ее окрестности.

Определение 1: Функция y=f(x) называется непрерывной в точке x₀, если она определена в этой точке и . x=x-x₀ – приращение аргумента, y=f(x)-f(x₀)=f(x₀+x)-f(x₀) – приращение функции.

Определение 2. Функция y=f(x) называется непрерывной в точке x₀, если б/м приращению аргумента соответствует б/м приращение функции, т.е. .

Определение 3. Функция y=f(x) называется непрерывной в точке x₀, если она определена в этой точке, оба односторонних предела существуют, конечны, равны между собой и равны значению функции в этой точке, .

Определение. Функция y=f(x) называется непрерывной на промежутке, если она непрерывна в каждой точке этого промежутка.