
- •Справочный материал по учебной дисциплине «Линейная алгебра. Аналитическая геометрия. Начала анализа» Матрицы.
- •Возведение матрицы в целую положительную степень
- •Свойства транспонирования матрицы
- •Определители квадратных матриц
- •Свойства обратных матриц
- •Общие понятия системы линейных уравнений
- •Метод обратной матрицы
- •Базис векторного пространства
- •Координаты вектора в данном базисе.
- •Координаты точки, радиус- вектор точки. Длина вектора.
- •Проекция вектора на ось.
- •Скалярное произведение векторов и его свойства
- •Приложения скалярного произведения.
- •Векторное произведение двух векторов.
- •Свойства векторного произведения.
- •Выражение векторного произведения в координатах.
- •Смешанное произведение векторов.
- •Сфера в пространстве.
- •Плоскость в пространстве.
- •Взаимное расположение двух плоскостей.
- •Понятие функции, способы задания функции.
- •Основные характеристики функции.
- •Числовые последовательности и их пределы.
- •Сходящиеся и ограниченные последовательности.
- •Бесконечно малые и бесконечно большие последовательности.
- •Свойства сходящихся последовательностей.
- •Предел функции.
- •Бесконечно малые и бесконечно большие функции и их свойства.
- •Арифметические операции с пределами.
- •Следствия из второго замечательного предела.
- •Сравнение бесконечно малых.
- •Непрерывность функции.
- •Свойства непрерывных функций.
- •Точки разрыва и их классификация.
- •Теоремы о непрерывных функциях.
- •Производная функции одной переменной.
- •Правила вычисления производной.
- •Уравнение касательной и нормали к кривой.
- •Производная сложной функции.
- •Производная обратной функции.
- •Дифференциал, его геометрический смысл, правила вычисления.
Базис векторного пространства
Определение. Упорядоченная совокупность линейно независимых векторов -мерного векторного пространства называется базисом этого пространства.
ТЕОРЕМА (о разложении вектора по базису) Каждый вектор линейного пространства можно представить, и притом единственным образом, в виде линейной комбинации векторов базиса.
Координаты вектора в данном базисе.
Рассмотрим
в линейном пространстве размерности
базис
 .
Любой
вектор линейного пространства разлагается
в линейную комбинацию базиса
.
Любой
вектор линейного пространства разлагается
в линейную комбинацию базиса
 ,
принадлежит
линейному пространству.
,
принадлежит
линейному пространству.
Определение:
Упорядоченный набор чисел
 ,
участвующий в разложении вектора по
базису
называется
координатами
этого вектора
в данном базисе.
,
участвующий в разложении вектора по
базису
называется
координатами
этого вектора
в данном базисе.
 –
координаты вектора линейного пространства.
–
координаты вектора линейного пространства.
Операции над векторами:
1) Для того, чтобы сложить два вектора линейного пространства в координатной форме нужно сложить их соответствующие координаты.
2) Чтобы вектор в координатной форме умножить на число нужно каждую координату умножить на это число.
Система
векторов называется
ортогональной,
если
называется
ортогональной,
если

при
 ;
нормированной,
если
для
всех
;
нормированной,
если
для
всех
 .
Если
векторы системы ортогональны и
нормированы,
они называются ортонормированными.
.
Если
векторы системы ортогональны и
нормированы,
они называются ортонормированными.
Определение: Упорядоченная тройка некомпланарных векторов называется правоориентированной или просто правой, если из конца третьего вектора кратчайший поворот от первого ко второму виден против хода часовой стрелки. В противном случае тройка векторов называется левоориентированной.
Координаты точки, радиус- вектор точки. Длина вектора.
Возьмем в пространстве произвольную точку М(х, у, z). Первая координата х – абсцисса ‒ это проекция т. М на ось ОХ. Вторая у – ордината – это проекция т. М на ось ОУ. Третья z – аппликата – на ось OZ.
Определение: Вектор, соединяющий начало координат т. О с произвольной точкой пространства называется радиус- вектор этой точки. координаты радиус-вектора точки совпадают с координатами самой точки ОМ= (x, y, z).
Чтобы найти координаты вектора нужно из координат конца вектора вычесть соответствующие координаты начала вектора.
Если
даны две точки плоскости и
и ,
то длину отрезка
,
то длину отрезка можно
вычислить по формуле
можно
вычислить по формуле .
Если даны две точки плоскости
.
Если даны две точки плоскости и
и ,
то длину отрезка
можно
вычислить по формуле
,
то длину отрезка
можно
вычислить по формуле .
.
Длина
вектора вычисляется по формуле

Проекция вектора на ось.
Определение: Проекцией вектора на ось называется число, модуль которого равен проекции на эту ось отрезка, задающего вектор, причем число берется со знаком «+», если координата конца вектора больше координаты начала вектора, и со знаком «-», если координата начала больше координаты конца.
Скалярное произведение векторов и его свойства
Определение:
Скалярным
произведением двух векторов
называется число
равное произведению длин этих векторов
(модулей) на косинус угла между векторами.
 .
.
1°
коммутативность:

2°
условие перпендикулярности:
 ;
;
 .
.
3°
 .
.
4°
 .
.
5°
скалярный квадрат:
 .
.
Пусть
заданы два вектора
 и
и
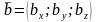 .
.
Скалярное
произведение двух ненулевых векторов
равно сумме произведений соответствующих
координат этих векторов:

Угол
между векторами
 ,или
в координатной форме
,или
в координатной форме
 .
.
