Справочный материал по учебной дисциплине «Линейная алгебра. Аналитическая геометрия. Начала анализа» Матрицы.

Определение. Матрицей с размерами называется прямоугольная таблица чисел, содержащая строк и столбцов. Числа, составляющие матрицу, называются элементами матрицы. Матрицы обычно обозначают заглавными буквами латинского алфавита, например, А, В, С,..., а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: 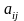где — номер строки, — номер столбца.

Виды матриц: нулевая; матрица-строка; матрица-столбец; квадратная; диагональная; единичная; треугольная; расширенная; равные

Основные действия над матрицами.

1. Сложение матриц одинакового размера. Чтобы найти сумму матриц одинакового размера, нужно сложить их соответствующие элементы. c_ij = a_ij + b_ij

Для суммы выполняется свойство коммутативности: С = А + В = В + А.

2. Вычитание матриц одинакового размера. Чтобы найти разность матриц одинакового размера, нужно из каждого элемента матрицы-уменьшаемого вычесть соответствующие элементы матрицы-вычитаемого. c_ij = a_ij - b_ij

3. Умножения (деления) матрицы на число. Чтобы умножить (поделить) матрицы любого размера на произвольное число, нужно каждый элемент матрицы умножить на это число.

4. Умножение матриц. Произведением матриц называется матрица, элементы которой могут быть вычислены по формуле .

Свойства операции умножения матриц.

1)Умножение матриц не коммутативно, т.е. АВ  ВА. Если соотношение АВ=ВА выполняется, то матрицы называются перестановочными.

2) Для любых матриц выполняются следующее свойство:AO = O; OA = O,

3) Операция перемножения матриц ассоциативна, если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство: (АВ)С=А(ВС).

4) Операция умножения матриц дистрибутивна по отношению к сложению, А(В+С) и (А+В)С, то соответственно: А(В+С)=АВ+АС; (А+В)С=АС+ВС.

5) Если произведение АВ определено, то для любого числа  верно соотношение: (AB) = (A)B = A(B).

6) Произведение двух ненулевых матриц может дать нулевую матрицу,

Возведение матрицы в целую положительную степень

Возведение матрицы в целую положительную степень сводится к произведению одинаковых матриц: ( раз).

Транспонирование матриц. Матрицу В называют транспонированной матрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.

Свойства транспонирования матрицы

1) ; 2) ; 3) ; 4) .

Определители квадратных матриц

Определителем матрицы первого порядка назовем число Определителем матрицы второго порядка назовем число, равное

Определителем матрицы третьего порядка назовем число, равное

Минором данного элемента определителя n-ого порядка называется определитель (n-1)-ого порядка, получаемый из данного определителя путём вычеркивания той строки и того столбца, на пересечении которых стоит данный элемент.

Алгебраическим дополнение любого элемента определителя равняется минору этого элемента, взятому со знаком «+», если сумма номеров строки и столбца, на пересечении которых стоит данный элемент есть число чётное, и со знаком «-» в противном случае.

Матрица называется невырожденной, если ее определитель отличен от нуля, т.е. _.В противном случае она называется вырожденной.

Определение. Матрица называется обратной по отношению к квадратной матрице , если выполняется равенство

ТЕОРЕМА (о существовании обратной матрицы) Обратная матрица существует и единственна тогда и только тогда, когда исходная матрица невырожденная.