11. Интервальные оценки. Методы нахождения интервальных оценок.

Интервальный метод оценивания параметров распределения случайных величин заключается в определении интервала (а не единичного значения), в котором с заданной степенью достоверности будет заключено значение оцениваемого параметра. Интервальная оценка характеризуется двумя числами – концами интервала, внутри которого предположительно находится истинное значение параметра. Иначе говоря, вместо отдельной точки для оцениваемого параметра можно установить интервал значений, одна из точек которого является своего рода "лучшей" оценкой. Интервальные оценки являются более полными и надежными по сравнению с точечными, они применяются как для больших, так и для малых выборок. Совокупность методов определения промежутка, в котором лежит значение параметра, получила название методов интервального оценивания. Методы интервального оценивания:

12. Элементы теории корреляции.

Корреляция или корреляционная зависимость - статистическая взаимосвязь двух или более случайных величин. При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин. Математической мерой корреляции двух случайных величин служит корреляционное отношение {\displaystyle \mathbf {\eta } }либо коэффициент корреляции. {\displaystyle \mathbf {R} }В случае если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической. Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные. Так, для измерения переменных с интервальной и количественной шкалами необходимо использовать коэффициент корреляции Пирсона: формула: 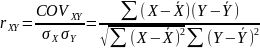, где  ,   — среднее значение выборок. Коэффициент корреляции изменяется в пределах от минус единицы до плюс единицы. Если по меньшей мере одна из двух переменных имеет порядковую шкалу, либо не является нормально распределённой, необходимо использовать ранговую корреляцию Спирмена: формула: ,

где n— кол-во ранжируемых признаков (показателей, испытуемых). D — разность между рангами по двум переменным для каждого испытуемого. Σ(D²) — сумма квадратов разностей рангов. Или {\displaystyle \mathbf {\tau } } (тау) Кендалла: В упрощенном виде формулу коэффициента корреляции Кендалла можно записать как: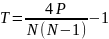 . При наличии связанных рангов формула изменяется с учетом поправки на связанные ранги: ,

где P(p) — число совпадений, P(q) — число инверсий, N — объем выборки,   — поправка на связи рангов переменной X,   — поправка на связи рангов переменной Y.

Основные задачи теории корреляции:

1. определить есть ли связь между случайными величинами, если есть, то найти уравнение зависимости (уравнение регрессии);

2. определить силу (тесноту) связи между случайными величинами. Для определения самого факта связи между случайными величинами и тесноты связи служит коэффициент корреляции.

Уравнение регрессии позволяет предсказать, какие изменения в среднем будет претерпевать признак при изменении другого признака. Если уравнения регрессии являются линейными, то есть графиками будут прямые линии, то корреляционная зависимость называется линейной..