8. Эмпирические (выборочные) и теоретические моменты и их взаимосвязь.

Выборочные моменты в математической статистике — это оценка теоретических моментов распределения на основе выборки.

9. Меры изменчивости. Вариация.

К мерам изменчивости переменной в статистике относятся: размах, дисперсия, среднее квадратическое (стандартное) отклонение и среднее линейное отклонение, коэффициент вариации. Вариация - количественное различие значений одного и того же признака у отдельных единиц совокупности. К абсолютным показателям вариации относят: размах вариации; среднее линейное отклонение; среднее квадратическое отклонение; дисперсию. Размах – разница между наибольшим и наименьшим результатами наблюдений. Размах показывает разброс значений в совокупности данных. Если размах большой, то значения в совокупности сильно разбросаны; если размах – небольшая величина, то значения в совокупности лежат близко друг к другу. Формула: R=X_max-X_min ;

Дисперсия (среднее квадратическое отклонение в квадрате) в статистике определяется как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической.

Среднее линейное отклонение d вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Эта величина определяется как средняя арифметическая из абсолютных значений отклонений от средней. Так как сумма отклонений значений признака от средней величины равна нулю, то все отклонения берутся по модулю. Формула среднего линейного отклонения (простая): =

Формула среднего линейного отклонения (взвешенная):

Относительные показатели вариации рассчитываются как отношение размаха вариации к средней величине признака (коэффициент осцилляции), отношение среднего линейного отклонения к средней величине признака (линейный коэффициент вариации), отношение среднего квадратического отклонения к средней величине признака (коэффициент вариации) и, как правило, выражаются в процентах.

Формулы расчета относительных показателей вариации:

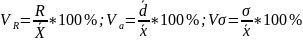
где V_R - коэффициент осцилляции;

V_α - линейный коэффициент вариации;

V_σ - коэффициент вариации.

Совокупность считается однородной если коэф. вариации не превышает 33%

10. Дисперсия и её свойства.

Дисперсия (среднее квадратическое отклонение в квадрате) в статистике определяется как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам взвешенной и простой дисперсии:

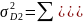
Более удобно вычислять дисперсию по формуле: , которая получается из основной путем несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней. Свойства дисперсии:

1. если из всех вариант вычесть какое-либо число, то дисперсия от этого не изменится; 

2. если все значения вариант разделить на какое-либо число, то дисперсия уменьшится в 2 раз;

3. если исчислить средний квадрат отклонений от какого-либо числа с неравного средней арифметической, то он будет больше дисперсии;

4. дисперсия постоянной величины равна;

5. постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат;

6. дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин;

7. дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин. Если статистическая совокупность разбита на группы или части по изучаемому признаку, то для такой совокупности могут быть исчислены следующие виды дисперсии: групповые (частные), средне групповые (частных), и межгрупповая.

Общая дисперсия – отражает вариацию признака за счет всех условий и причин, действующих в данной статистической совокупности. Групповая дисперсия - равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы, называемой групповой средней. При этом групповая средняя не совпадает с общей средней для всей совокупности. Групповая дисперсия отражает вариацию признака только за счет условий и причин, действующих внутри группы. Средняя групповых дисперсий - определяется как среднее взвешенное арифметическое из дисперсий групповых, причем весами являются объемы групп. Межгрупповая дисперсия - равна среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия характеризует вариацию результативного признака за счет груgпировочного признака. Между рассмотренными видами дисперсий существует определенное соотношение: общая дисперсия равна сумме средней групповой и межгрупповой дисперсии. Это соотношение называется правилом сложения дисперсии.