МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПЕТРА ВЕЛИКОГО

Институт энергетики и транспортных систем

Центр заочного обучения

Курсовая работа

на тему: Переходные процессы в линейных и нелинейных электромагнитных систем

по дисциплине: Дополнительные главы теоретических основ электротехники

Выполнил: студент гр. з 13241/21 ______________/Борисов Д.А./ (И. О. Фамилия)

Проверил: ____________/Коровкин Н.В./ (И. О. Фамилия)

Санкт-Петербург

2017г.

Оглавление

Введение 5

Задание 6

1. Схемы замещения и их параметры 8

1.1 Схема источника ЭМЭ и ее параметры 8

1.2 Схемы замещения линии 1 8

1.2.1 Линия 1. Начальный участок 9

1.2.2 Линия 1. Конечный участок. 9

1.3 Схема подстанции П1 и ее параметры 10

1.4 Схема замещения линии 2 10

1.5 Схема нагрузки П2 второй линии и ее параметры 11

1.6 Схема замещения линии 3 12

1.7 Схема нагрузки П3 третьей линии и ее параметры 12

2. Расчет напряжений между заданными узлами в системе линий 14

2.1 Входное сопротивление второй линии, нагруженной на сопротивление Zп2 14

2.2 Входное сопротивление третьей линии, нагруженной на сопротивление Zп3 14

2.3 Эквивалентное сопротивление нагрузки первой линии 15

2.4 Входное сопротивление конечного участка первой линии 15

2.5 Расчет напряжения между заданными узлами в линии 1 16

2.6 Расчет максимальных напряжений на всех зажимах линии в установившемся синусоидальном режиме 18

2.6.1 Зажимы 1-1 18

2.6.2 Зажимы 2-2 18

2.6.3 Зажимы 3-3 19

2.6.4 Зажимы 4-4 19

2.6.5 Зажимы 5-5 19

3. Расчет переходного процесса в системе линий при включении ее под синусоидальное напряжение 21

3.1 Оценка изменения напряжения источника за расчетное время 21

3.2 Определение постоянного напряжения, под которое включается система линий 22

3.3 Обозначения принятые при расчете переходных процессов в линиях с распределенными параметрами 23

3.4 Схема замещения для расчета процессов на подстанции П1 и ее параметры 23

3.5 Расчет переходного процесса в схеме замещения на подстанции П1 24

3.6 Определение напряжений и токов на входе и выходе П1 25

3.7 Определение волн напряжения и тока, отраженных от подстанции П1 и преломленных через подстанцию в линию 2 и в линию 3 26

3.8 Расчет переходных процессов в нагрузке П2 линии 2 27

3.8.1 Расчет операторным методом 27

3.8.2 Расчет входного тока нагрузки П2 в переходном процессе с помощью интеграла Дюамеля 29

3.3.9 Определение напряжение и тока отраженной от нагрузки П2 волны 30

3.10 Расчет переходных процессов в нагрузке П3 линии 3 31

3.11 Нахождение распределения напряжения и тока вдоль линий в момент времени, когда отраженная от нагрузки П2 волна пройдет расстояние s 33

3.11.1 Линия 1 34

3.11.2 Линия 2 34

3.11.3 Линия 3 35

3.11.4 Эпюры распределения напряжения и тока воль линий в заданный момент времени 35

Заключение 39

Список использованной литературы 40

Введение

Постоянное развитие энергоемких производств связано с увеличением потребления электроэнергии в различных регионах страны, многие их которых расположены на значительных расстояниях от электростанций. Поэтому проектирование линий электропередач является актуальной задачей электротехники. Эта задача с электротехнической точки зрения весьма сложна, что связано с особенностями электромагнитных процессов в таких устройствах.

Параметры электрических цепей непрерывно распределены вдоль участков цепи. Однако для многих цепей можно принять допущение о том, что параметры сосредоточенны в определенных участках цепи. Критерием допустимости такого предположения является соотношение между интервалом времени распространения электромагнитных волн вдоль цепи и интервалом времени, в течение которого токи и напряжения на величину, сопоставимую с временем их полного изменения в рассматриваемом процессе.

Электрические цепи, в которых напряжения и токи заметно изменяются вдоль их длины, необходимо рассматривать как цепи с распределенными параметрами или длинные линии.

Задание

Вариант	L2, км	S1/l1	S2/l2
33	40	0,6	0,1

Таблица 1

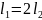
Таблица 2

Таблица 3

Таблица 4

Для П3:

Для П2

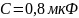
1. Схемы замещения и их параметры

Схема рассматриваемой системы линии имеет следующий вид:

1.1 Схема источника ЭМЭ и ее параметры

Для расчета синусоидального режима представим входное напряжение в комплексной форме:

1.2 Схемы замещения линии 1

Поскольку при анализе установившегося синусоидального режима необходимо определить напряжения в некоторых заданных точках линии, либо на их оконечных зажимах, а волновые процессы, происходящие в самих линия, не рассматриваются, то можно представить линии в виде эквивалентных схем с сосредоточенными параметрами, в которых выделены интересующие нас точки. Воспользуемся Т-образными схемами замещения линий и их частей.

1.2.1 Линия 1. Начальный участок

Для того, чтобы определить напряжение между заданными точками К1 и К2 первой линии, разобьем ее на два участка. Первый (начальный) участок длиной 20 км от начала линии до точек К1 и К2 заменяем схемой на рисунке 1а. Схема на рисунке 1б эквивалентна второму (конечному участку длиной 20 км от точек К1 и К2 до конца линии.

A-параметры четырехполюсника, моделирующего первый участок:

Далее находим параметры схемы замещения первого участка первой линии

1.2.2 Линия 1. Конечный участок.

Поскольку в рассматриваемом примере длины участков, на которые разбивается первая линия, равны, то равны и параметры четырехполюсников, заменяющих эти участки.

Далее находим параметры схемы замещения второго участка первой линии

1.3 Схема подстанции П1 и ее параметры

1.4 Схема замещения линии 2

Вторую линию рассматриваем как четырехполюсник, который заменяем Т-образной эквивалентной схемой:

Аналогично тому, как это было сделано выше, определяем параметры четырехполюсника:

Далее находим параметры схемы замещения второй линии

1.5 Схема нагрузки П2 второй линии и ее параметры

Комплексные сопротивления отдельных участков этой схемы:

Эквивалентное сопротивление нагрузки второй линии равно

1.6 Схема замещения линии 3

Третью линию рассматриваем как четырехполюсник, который заменяем Т-образной эквивалентной схемой:

Аналогично тому, как это было сделано выше, определяем параметры четырехполюсника:

Далее находим параметры схемы замещения третьей линии

1.7 Схема нагрузки П3 третьей линии и ее параметры

Нагрузкой линии является сопротивление:

2. Расчет напряжений между заданными узлами в системе линий

Расчет установившегося режима в полной схеме, составленной из перечисленных выше схем замещения линий и схем источника И1, подстанции П1, нагрузок П2 и П3, может быть выполнен любым известным методом расчета сложных электрических цепей. Так как в подлежащей анализу схеме действует только один источник ЭМЭ, можно достаточно просто выполнить расчет токов и напряжений в ней , например, путем постепенных эквивалентных преобразований ее сопротивлений к эквивалентном сопротивлению относительно зажимов источника ЭДС.

2.1 Входное сопротивление второй линии, нагруженной на сопротивление Zп2

Соответствующий фрагмент полной схемы имеет вид:

Входное сопротивление равно

2.2 Входное сопротивление третьей линии, нагруженной на сопротивление Zп3

Соответствующий фрагмент полной схемы имеет вид:

Входное сопротивление равно

2.3 Эквивалентное сопротивление нагрузки первой линии

Соответствующая расчетная схема имеет вид

Эквивалентное сопротивление нагрузки 2 на линию 1 равно

Так как сопротивление нагрузки 2 на первую линию и входное сопротивление 3 включены параллельно, то входное сопротивление системы равно

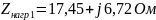
4. Входное сопротивление конечного участка первой линии

Схема для расчета входного сопротивления конечного участка линии 1 с нагрузкой линии имеет вид:

Это сопротивление равно

4. Расчет напряжения между заданными узлами в линии 1

Схема для расчета напряжения в заданном месте первой линии (между К1 и К2) имеет вид:

Определим сопротивление всей системы линий Zвх по отношению к зажимам источника ЭДС:

Входной ток равен

Ток, протекающий по сопротивлению равен

Напряжение в узле AB равно

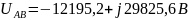
Будем варьировать величину волнового сопротивление третьей линии в заданных пределах, от 280 до 500 Ом, соответствующих реальным значениям сопротивлений воздушных линий. Результаты расчета сведем в таблицу 1 и представим графически

Таблица 1

, Ом	, кВ	, кВ
280		31577,4
300		31685,1
320		31792,8
340		31900,4
360		32007,94
380		32115,32
400		32222,52
420		32329,51
440		32436,25
460		32542,71
480		32648,7
500		32754,7

Из графика видно, что зависимость напряжения от сопротивления носит монотонный характер, близкий к линейному. При этом в рассмотренном диапазоне изменения сопротивления, изменение искомого сопротивление составляет 3,6% от его значения при сопротивлении 280 Ом. Таким образом для дальнейших исследований волновое сопротивление третьей линии выбрано равным 280 Ом.

4. Расчет максимальных напряжений на всех зажимах линии в установившемся синусоидальном режиме

Для дальнейших расчетов необходимо пересчитать все параметры схемы замещения, начиная с того места, где учитывается выбранное значение искомого сопротивления. С учетом нового значения сопротивления третьей линии равного 280 Ом, входное сопротивление цепи принимается равным

1. Зажимы 1-1

Из приведенной выше схемы для комплекса напряжения на входных зажимах следует, что

2. Зажимы 2-2

Определим ток :

Определим напряжение нагрузки 12

Определим ток :

Определим напряжение на зажимах 2-2

3. Зажимы 3-3

Определим напряжение на входных зажимах линии 2:

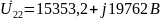
Амплитуда равна

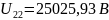
2.6.4 Зажимы 4-4

Находим комплекс тока

Найдем напряжение на зажимах 4-4

Амплитуда равна

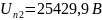
2.6.5 Зажимы 5-5

Находим комплекс тока

Найдем напряжение на зажимах 5-5

Амплитуда равна

Сведем напряжения на зажимах в таблицу 2

Таблица 2

Линия №	Зажимы №
1	1-1
	2-2
2	3-3
	4-4
3	2-2
	5-5

Таким образом, максимальное напряжение наблюдается на входных зажимах линии 1. На остальных зажимах напряжения различаются между собой не более, чем на 25%.