Задача 3

Тема: «Статистическая обработка результатов многократных измерений»

3.1 Теоретическая часть

Статистическая обработка результатов многократных измерений основывается на использовании большого объёма практически полученной апостериорной информации.

Цель статистической обработки результатов измерений: получить более достоверную информацию о том, в каких границах можно ожидать появление измеряемой случайной физической величины (например: измеряемого размера).

При этом решаются три задачи:

оценивание области неопределённости исходных экспериментальных данных;

нахождение более точного усреднённого результата измерений;

оценивание погрешности этого усреднённого результата, то есть нахождение более узкой области неопределённости числового появления размера.

3.2 Определения

Статистическая обработка результатов измерений заключается в определении границ доверительного интервала в размерном ряду, в которых может появиться ожидаемый размер объекта измерения.

Апостериорная информация – та, которая получена путём проведения практических измерений.

Доверительный интервал – границы числового ряда значений случайной величины, внутри которых с определённой вероятностью будет находиться математическое ожидание этой случайной величины. Для закона нормального распределения случайных величин эти границы расположены симметрично их среднему арифметическому значению (например, измеряемый диаметр деталей круглой формы: его размер – это случайная величина).

Доверительная вероятность – вероятность, соответствующая этому доверительному интервалу.

Диапазон рассеивания размеров – разность между максимальным и минимальным размерами.

Интервалы в диапазоне рассеивания размеров – отрезки оси размеров, делящие диапазон рассеивания на равные части.

Случайная величина – которая в результате опыта может принять то или иное значение, не известное заранее (например, измеряемый диаметр одинаковых деталей круглой формы).

Дискретная величина – случайная величина, которая может принять только раздельное, отделенное от соседних величин из размерного ряда значение величины (например, возможное число очков при бросании во время игры в кости).

Действительная величина – числовой результат измерения.

Выборка – некоторое небольшое количество измерений, проделанное для того чтобы по их результатам судить о более полном диапазоне рассеивания измеренной величины.

Гистограмма – график, в прямоугольных осях «частость – диапазон рассеивания измеренных значений», состоящий из вертикальных прямоугольников различной высоты и эмпирической ломаной кривой, соединяющей серединки верхних перекладин прямоугольников, отображающей закон распределения измеряемых случайных величин.

3.3 Порядок проведения и математической обработки результатов статистических измерений

Для того чтобы проверить большую партию изготовленных одинаковых деталей по какому-то одному размеру не требуется измерять каждую деталь, достаточно сделать это , например, для каждой десятой детали (10%), то есть произвести выборку и по результатам этой проверки судить о годности остальных 90%.

При измерениях одного и того же размера в выборке, так же как и во всей партии деталей измеренные значения несколько отличаются друг от друга. Если количество измерений в выборке невелико, то для определения доверительного интервала более полного разброса их значений необходимо провести статистическую обработку результатов измерений.

Статистическая обработка результатов измерений производится следующим образом.

Имеются следующие исходные данные:

номинальный размер детали Х и его допуск T, на чертеже обозначаемые как Х±Т;

N – количество измеренных деталей, один и тот же размер которых несколько отличается между собой по величине или равный у некоторых деталей. Обычно в исходных данных задачи результаты измерений записаны в хаотическом порядке.

Решение

1) Располагают полученные в процессе N измерений действительные значения X_i в порядке возрастания их величины и тем самым получают ранжированный ряд случайных дискретных величин: X₁; X₂…X_N.

2) Диапазон рассеивания R определяется как разность между максимальной X_MAX и минимальной X_MIN величинами действительных значений измерений:

R = X_MAX – X_MIN .

3) Полученное значение диапазона рассеивания разбивают на K интервалов (рекомендуется 7 – 12 интервалов). Задавшись числом интервалов, рассчитывают дискретный шаг интервалов по формуле:

P = R/K .

4) Строят оси гистограммы абсцисс и ординат. Масштаб гистограммы выбирают таким, чтобы её высота относилась к основанию примерно как 5:8. На оси абсцисс в начале координат ставят значение X_1, равное X_MIN, а в конце оси ставят значение X_N , равное X_MAX

Полученный отрезок оси делят на K равных по длине интервалов и записывают напротив каждой границы её числовое значение: X_1; X₁₊P; (X₁₊P)₊P и так далее. Конечное значение должно совпасть с X_N.

5) Для каждого интервала подсчитывают число измерений n_j, имеющих величину, находящуюся в пределах между меньшей, например, X₁ и большей X₁₊P границами этого интервала и так далее.

6) После этого для каждого интервала рассчитывают среднее арифметическое значение X j_СР в группе измерений j-того интервала, а также частость числа измерений

n_j /(N – 1) в данном интервале.

Результаты измерений и расчётов пунктов 1), 5) и 6) заносят в таблицу.

Пример таблицы с записями значений случайной величины при N=16 и К=7 приведён в таблице 3.1 (вместо букв «ранжированный ряд» надо поставить измеренные величины по возрастанию X₁; X₂…X₁₆. В первый интервал вошли X₁ и X₂, во второй – X_3, X₄ и X₅. И так далее для каждого интервала.

Таблица 3.1 – Записи значений случайной величины X_{i (ИТОЕ)}

Номер измерения

1

2

3

4

5

6

7

8

9

10

Хi (ИТОЕ)

р

а

н

ж

и

р

о

в

а

н

X jСР (ЖИТОЕ)

(р+а)/2

(н+ж+и)/3

(р+о+в+а+н)/5

nj (ЖИТОЕ)

2

3

5

nj /(N – 1)

2/15

3/15

1/3

Продолжение таблицы 3.1

Номер измерения	11	12		13	14	15	16
Xi (ИТОЕ)	н	ы		й	р	я	д
X jСР (ЖИТОЕ)	(н+ы)/2		(й+р+я+д)/4
nj (ЖИТОЕ)	2		4
nj /(N – 1)	2/15		4/15

где X_i – значение i-того измерения;

n_j – число измерений, имеющих величину, находящуюся в пределах между меньшей и большей границами j-того интервала;

n_j /(N – 1) – частость числа измерений в данном интервале.

X _jСР – среднее арифметическое значение измерений j-того интервала (рассчитывается для каждого интервала):

,

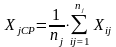Х_ij – (икс итое-житое) – измерение X_i в j-том интервале_, то есть находящееся в пределах между меньшей и большей границами j-того интервала;

n_j /(N – 1) – частость числа измерений в данном интервале.

_{В таблице в приведенном примере всего 5 размерных интервалов вместо 7 потому что, например, в двух интервалах значений размеров не оказалось: в первом интервале – 2 значения измерений (1 и 2), во втором – 3 (3, 4 и 5) и так далее, а в четвёртом и шестом, например, их нет. Пустые интервалы в таблице не указываются.}

7) Над каждым интервалом строят прямоугольник, соответствующий по своей высоте величине рассчитанной частости n_j /(N – 1) для этого интервала, после чего строят эмпирическую ломаную кривую, соединяя серединки верхних перекладин прямоугольников. Если в каком-то интервале частость равна нулю, то ломаную кривую соединяют с серединкой интервала на оси абсцисс.

8) Определяют среднее арифметическое значение всех замеренных действительных значений величин:

.

Рисунок – Пример построения гистограммы

9) Рассеяние значений случайных величин в выборке из N измерений относительно эмпирического (опытного, практического) группирования их по интервалам характеризуется уточнённым эмпирическим средним квадратическим отклонением, которое определяется по формуле:

.

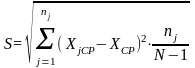10) По результатам выборки устанавливают границы, внутри которых с определённой вероятностью будет находиться математическое ожидание F(x) случайной величины Х. Эти границы определяют доверительный интервал, который зависит от доверительной вероятности β. В общем случае при малой выборке и различной доверительной вероятности доверительный интервал в своих меньшей и большей границах выразится следующими неравенствами:

Х_СР – t_δσ_{х ср} F(х) Х_СР + t_δσ_{х ср ,}

где σ_{х ср} – среднее квадратическое отклонение для распределения средних арифметических величин:

σ_{х ср} ;

t_δ – критерий Стьюдента, который для β=0,9 (90% доверительная вероятность) принимаем равным 1,75.

11) Сравнивают границы доверительного интервала с допуском на размер (он задан в условии задачи) и делают вывод о годности всей партии деталей. Для сравнения строят в примерном масштабе схему поля допуска заданного размера X и рядом наносят поле доверительного интервала.

Если границы доверительного интервала не выходят за пределы поля допуска, то партия деталей считается годной с доверительной вероятностью β.

12) Ответом на решение задачи является вывод о годности партии деталей: партия деталей годна или не годна с указанием сравниваемых величин большей и меньшей границ доверительного интервала и верхней и нижней границ поля допуска детали.