5. Оптимизация алгоритмов на графах

5.1 Алгоритм Дейкстры

Начнем с алгоритма Дейкстры. Суть оптимизации будет заключаться в следующем: Будем поддерживать кучу, в которой будут храниться минимальные пути от стартовой вершины, до каждой. Тогда вместо поиска минимального расстояния в массиве мы будем извлекать это значение из кучи за гораздо меньшее время. Когда в ходе алгоритма будут находиться более короткие пути, будем добавлять их в кучу. Алгоритм будет выполняться до тех пор, пока куча не станет пустой.

Проведем сравнительный анализ зависимости количества вершин от времени работы для разных плотностей графов. От 1 до 4 будем уменьшать плотность графа:

Рисунок 5.1: Плотность графа = 1

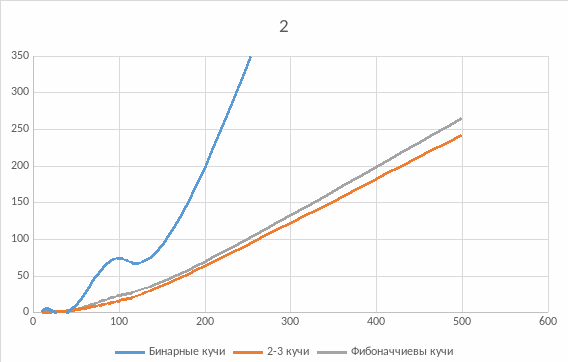
Рисунок 5.2: Плотность графа = 0.5

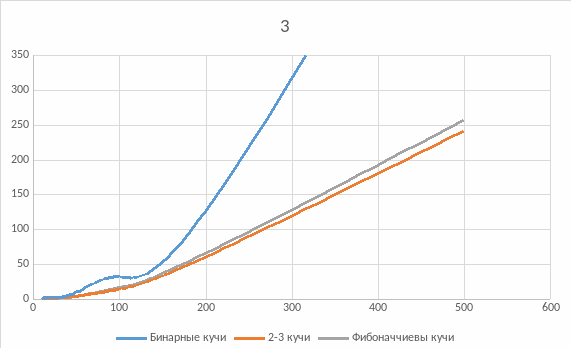
Рисунок 5.3: Плотность графа = 0.2

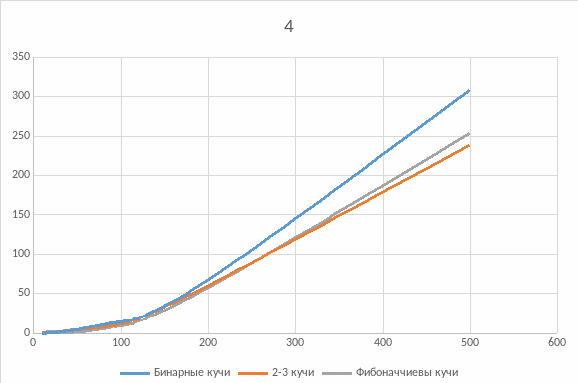
Рисунок 5.4: Плотность графа = 0.05

При уменьшении плотности графа графики стремятся к одинаково оптимальным решениям. Однако на плотных графах только 2-3 кучи дают заметный прирост по отношению к Бинарным кучам и до 20% по отношению к Фибоначчиевым кучам.

На разреженных графах все три структуры данных работают практически одинаково, однако 2-3 куча все равно дает немного лучший результат. Таким образом 2-3 куча является самой оптимально работающей в плане быстродействия при любых случаях по отношению к Бинарной и Фибоначчиевой куче.

5.2 Алгоритм Прима

Алгоритм Прима подразумевает выбор ближайшей вершины из множества доступных и не посещенных, поэтому и здесь имеет место оптимизация при помощи очереди с приоритетом. Механизм схожий с примененным в алгоритме Дейкстры: Сначала в очередь загружаем стартовую вершину, затем выгружаем все смежные с ней вершины в очередь, и так до тех пор, пока очередь не станет пустой или не пометим все вершины.

При тестировании не учитывался факт наличия остова, так как граф генерировался случайным образом. Если в графе нет остова, алгоритм отработает медленнее, так как условием выхода будет полное опустошение очереди, а в случае с наличием остова выход из алгоритма, как правило, возникает раньше. Также в тестировании используется реализация на массиве. На графиках 8-10 приведены результаты тестирования для плотного графа, графа с плотностью 0.5, и разреженного графа.

Рисунок 5.5: Алгоритм Прима на плотном графе.

Рисунок 5.6: Алгоритм Прима на графе плотностью 0.5.

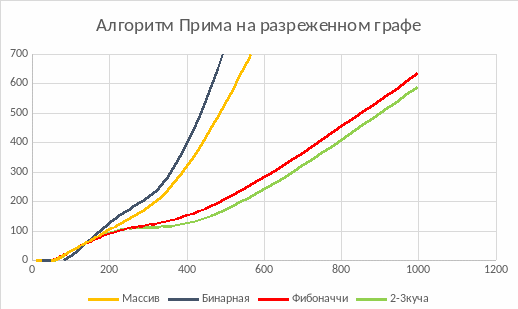
Рисунок 5.7: Алгоритм Прима на разреженном графе.

Из графиков видно что Бинарная куча, взятая из std::priority_queue не годится в целях оптимизации по скорости. Фибоначчиев куча и 2-3 куча жестко конкурируют, однако с ростом количества вершин 2-3 куча начинает превосходить кучу Фибоначчи.

Подведение итогов

Тестирование показало, что в среднем при оптимизации алгоритмов на графах прирост быстродействия при выборе 2-3 кучи достигает 20%. Мною также был рассмотрен алгоритм выбора ближайшего соседа для решения задачи коммивояжера, и сортировка кучей. В обоих случаях была отмечена приблизительно та же зависимости, что и при описанных в данной работе алгоритмах.

Все вышесказанное продемонстрировало стабильную и оптимальную работу 2-3 кучи по отношению к Бинарным и Фибоначчиевым кучам. Если Бинарные кучи все ещё занимают место лидера по критерию экономии памяти, то Фибоначчиевы кучи уступают 2-3 кучам по всем критериям. Класс алгоритмов на графах, в которых используется выбор приоритетного из множества замечательно оптимизируется при помощи 2-3 куч.

На данный момент времени 2-3 кучи менее популярны чем другие структуры данных, и это скорее всего обусловлено тем, что 2-3 кучи были описаны сравнительно недавно, и их реализация более трудоемкая. В сети интернет и литературных источниках информация почти отсутствует, поэтому я использовал первоисточник, из которого черпал идею, и проводил аналогию с другими кучами. На выходе получилась структура данных, которая способна улучшить быстродействие не только отдельных алгоритмов, но и разного рода систем массового обслуживания, и вообще всего, что связано с обработкой данных в порядке приоритета.

По данным тестирования можно вывести правило выбора очереди с приоритетом:

Бинарную кучу следует выбирать тогда, когда накладываются ограничения на требуемые ресурсы, либо, когда необходимо в условиях жесткого ограничения по времени реализовать рабочую очередь с приоритетом.

Кучу Фибоначчи следует выбирать тогда, когда предъявляются требования на быстродействие алгоритмов обработки информации, при этом реализацию нужно проводить в сжатые сроки. Также следует что должно быть известно, что вероятность операции удаления приблизительно равна операции вставки, либо если это не так, это существенным образом не отразится на работе системы в целом.

2-3 Кучу следует выбирать при тех же требованиях, что и кучу Фибоначчи, но если запас времени на реализацию больше, либо есть запас высококвалифицированных разработчиков, способных реализовать эту структуру данных в сжатые сроки.

Биномиальную кучу не следует использовать кроме специфических частных случаев.